0、提高数据样本质量
首先是确保数据采集的准确性与可靠性,也就是如何降低数据误差
- 系统误差是由测量工具不精确和测量方法选择不当造成的。这类误差我们可以通过校准工具或者选择更合适的测量方法来消除;
- 随机误差是由环境因素等外部不可控原因导致的,如温度、湿度、压力、电磁干扰等。无法预防,也无法从根本上消除。只有通过多闪重复实验来尽可能降低随机误差的比例;
- 过失误差是由操作人员的不履行正确采集操作规程、工作不认真甚至造假等人为因素造成的。这种误差是可以通过员工培训或管理手段避免的。
其次是采用科学的抽样方法。
正确的抽样会显著提高样本代表总体的水平。一般常用的抽样方法包括单纯随机抽样、系统抽样和分层抽样
单纯随机抽样。采用无放回的形式,随机抽取样本集合中的样本,直到达数量要求为止。这种抽样操作简便,公平性强,但不适合大样本集合,容易造成样本分布局部化,降低样本代表总体的水平。
系统抽样。首先将样本集合平均分为m组(m为采样数量),然后对每一组进行单纯随机抽样。该方法适合大样本,能够弥补单纯随机抽样局化的缺陷。但是对于数据按顺序有周期特征或单调递增(或递减)趋势特征时,将会产生明显的偏性。
分层抽样。先对样本集合根据样本的某种属性进行分组,然后在每组内按等比方式抽样。该方法适合为明显个体特征(如年龄、性别、职业等)的大样本,样本代表性较好,抽样误差较小。缺点是操作更复杂。
概率分布
建立X到y的高质量映射模型f的过程是很复杂的,我们需要用到不同的算法,比如回归、分类、神经网等等,无论使用哪种算法,为了降低模型的数据y’与真实的y之间的误差,我们需要保证X自变量数据集合和y因变量集合尽可能符合正态分布,也就是偏离值尽量少出现,而正常值出现的情况比较均匀,用这样的数据集拟合函数时各种情况会考虑到,函数的泛化能力就比较高。
是的,你没有看错!机器学习要想得到高质量模型,就要使样本数据保持正态分布。而现实往往不如人意,绝大多数情况往往不符合正态分布,而是偏态分布。
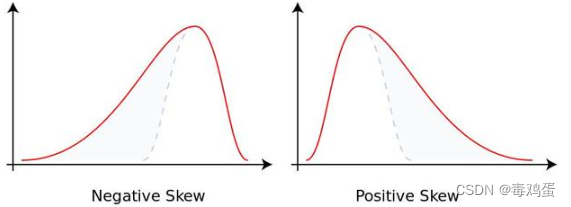
左图为负偏态(样本数据取大值得较多 ),右图为正偏态(样本取小值的较多)
如果样本的偏度比较大,就会造成模型偏差或方差过大,影响模型的精确水平和泛化能力,降低模型质量。
偏态数据的正态化常用方法有两种:
- 对于
因变量y而言,可以采用对数化方法,即y=log(y)
如果偏度很大,则对数函数的底数就大一些,过大容易调整过头,产生相反的偏态,一般来说取自然对数即可(Numpy.log1p())函数 - 对于
自变量集合X分布偏态的属性/字段,则使用box-cox()函数进行正态化(scipy.special.boxcox1p函数)。进行对数正态化.
相关链接:Box-Cox变换详解
当然对于分布比较复杂的情况,需要其他的一些 方法,如
倒数法、平方根法、指数函数法和三角函数法。
集中趋势和离散趋势
集中趋势
集中趋势是一组数据的代表值,和所有值差距不大是最好的: 平均数和中位数、众数
如果样本呈正态分布,那么集中趋势使用平均数或中位数表示均可,因为两者是相等的。
如果样本呈偏态分布,那么选择中位数更能反映数据的集中趋势。
通常情况下,
正偏态的中位数小于平均数,
负偏态的中位数大于平均数
离散趋势
离散趋势反映了样本数据之间的差异水平。反映离散趋势的统计指标一般包括标准差/方差、极差、四分位间距IQR和变异系数。
- 极差是样本最大值与最小值的差;
- 四分位间距IQR是75%分位数与25%分位数的差,显然四分位间距IQR一般要比极差小;
- 变异系数是标准差与均值的比值,通常认为如果变异系数
超过15%,则说明业务状况是很不稳定的。例如:变异系数是1.58,说明是极不稳定的。
除了变异系数是相对量化指标外,其它三个指标都是绝对量化指标。
因此,变异系数可以进行不同数据集离散程度的比较,而其它三个指标不可以,因为不同数据集的数据尺度有所差异
置信区间
通俗一点讲,如果置信度为95%(等价于显著水平a=0.05),置信区间为[a,b],这就意味着总体均值落入该区间的概率为95%,或者以95%的可信程度相信总体均值在这个范围内。
- 一般情况下当我们抽样的数量大于等于30时,可认为样本均值服从正态分布
- 如果样本数量小于30,我们可以根据中心极限定理,进行多轮抽样产生均值样本,计算置信区间。
中心极限定理:无论样本所属总体服务什么分布,对该样本进行n次随机采样,产生n个新的样本,那么这n个样本的n个均值所在总体服务正态分布。而且n越大,越接近正态分布。
#初始化样本
X=np.array([91,94,91,94,97,83,91,95,94,96,97,95,90,91,95,91,88,85,89,93])
#样本排序,为了适应下面的随机抽样函数
X=sorted(X)
#使用random模块的随机抽样函数sample,进行抽样。该函数有两个参数,第一个是样本集合,第二个是抽取数量
import random
#进行30轮随机抽样同时计算均值,形成新的正态分布的样本
n=30
X_new=[np.mean(random.sample(X, 10)) for i in range(n)]
#计算样本均值和标准差
mu,std=np.mean(X_new),np.std(X_new)
#求置信区间
[mu-std/np.sqrt(n)*1.96,mu+std/np.sqrt(n)*1.96]
# 最终估计的总体均值置信区间为[91.69, 92.18]。
相关性分析方法
相关性是量化不同因素间变动关联程度的指标。
在样本数据降维(通过消元减少降低模型复杂度,提高模型泛化能力)、缺失值估计、异常值修正方面发挥重要作用,是机器学习样本数据预处理的核心工具.
Pearson相关系数
相关系数是最早由统计学家卡尔·皮尔逊设计的统计指标,是研究变量之间线性相关程度的量。计算公式如下:

Numpy和Pandas都提供了Pearson相关系数的计算函数,分别为np.corrcoef()和Pandas.corr()

主对角线的值是两个变量的自相关系数,自然都是1,次对角线的值就是两组数据的Pearson相关系数值。我们可以看出耗电量和销售收入正相关性还是很高的,用Seaborn的回归图也能比较直观的看出两组数据的相关水平
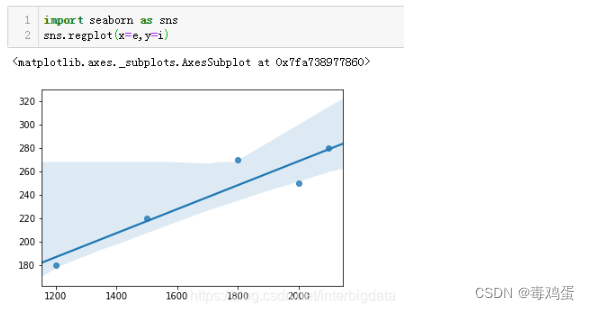
数据点比较紧密的集中在直线附近,这表明两组数据的相关性很高。
Pearson相关系统适合正态分布、连续随机变量、线性相关程度高的情况。
向量夹角余弦
把两组数据作为两个n维向量,通过计算两个向量的夹角余弦值,也可以衡量数据的相关程度,其取值范围也在[-1,1]之间。向量的夹角余弦值也称为向量余弦距离或向量相似度,其公式如下:

Spearman相关系数
Spearman相关系数又称秩相关系数,是利用两变量的秩次大小作相关分析,是一种非参数方法,对原始变量的分布不作要求,也没有线性相关要求。
Scipy中的spearmanr()函数可以帮助我们计算Spearman相关系数。
Spearman相关系数有如下特点:
- 属于非参数统计方法,适用范围更广。
- 对于服从Pearson相关系数的数据亦可计算Spearman相关系数,但统计效能要低一些。
- 秩次:样本数据正向排序后的序号(从1开始)
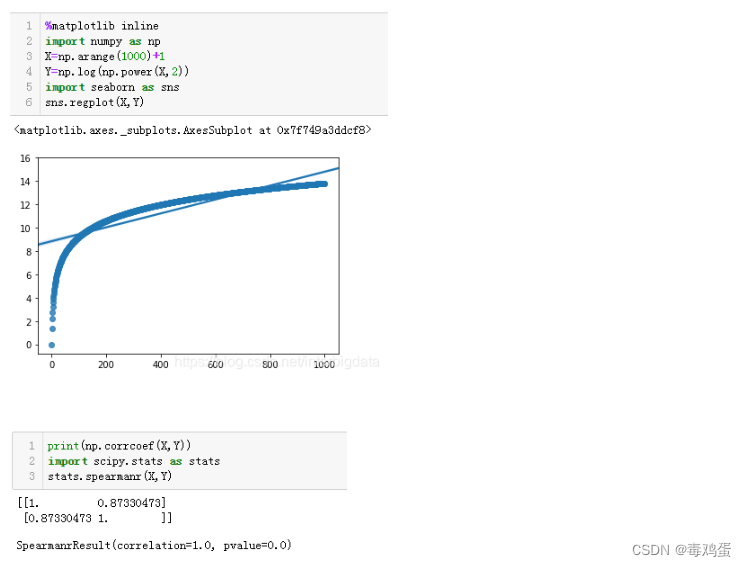
对于非线性相关的数据,Spearman相关系数要比Pearson相关系数更显著。
Kendall相关系数
肯德尔秩相关系数也是一种秩相关系数,不过它所计算的对象是分类有序/等级变量,如质量等级、考试名次等。对样本量小,有极端值的情况也更适用。其特点为:
- 1)如果两组排名是相同的,系数为1 ,两个属性正相关。
- 2)如果两组排名完全相反,系数为-1 ,两个属性负相关。
- 3)如果两组排名是完全独立的,系数为0。
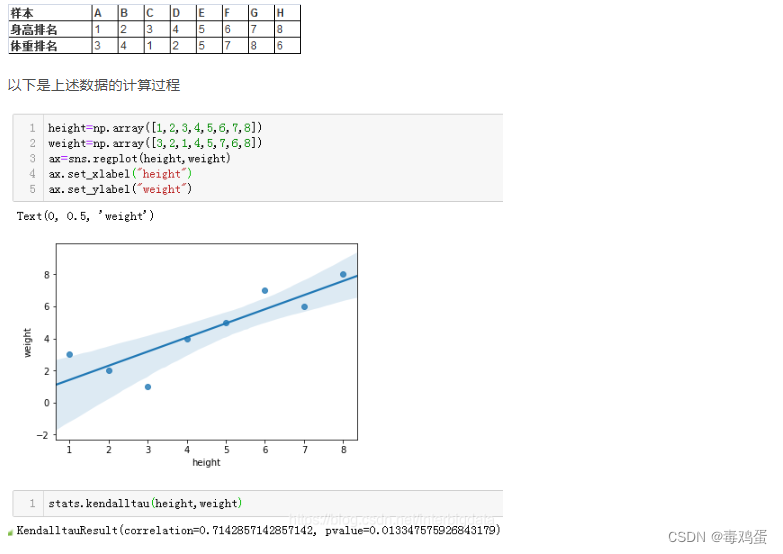
整体上,我们发现体重与身高大多数情况下有较强的相关性。
比较 总结
Pearson相关系统适合正态分布、连续随机变量、线性相关程度高的情况。- 对于
非线性相关的数据,Spearman相关系数要比Pearson相关系数更显著肯德尔秩相关系数对样本量小,有极端值的情况也更适用
下图直观的体现了三种相关系数的有效性。可以看出,在相关性极为明显(极相关或极不相关)的情况下,三者效果是无差异的。而对于相关性不太明确的情况(图3),Kendall相关系数更为保守一些。

相关链接: 相关性分析的五种方法
参考
https://blog.csdn.net/interbigdata/category_12020170.html