一、什么是堆排序?
堆排序就是将待排序元素以一种特定树的结构组合在一起,这种结构被称为堆。
堆又分为大根堆和小根堆,所谓大根堆即为所有的父节点均大于子节点,但兄弟节点之间却没有什么严格的限制,小根堆恰恰相反,是所有的根节点均小于子节点。
所以为了能够实现堆排序,第一个步骤就是将待排序的元素建成堆的形式,其次就是将建好的大根堆(小根堆)与堆的最后一个元素交换,然后再对新的堆进行向下的调整,但是在调整过程中,所有经过交换过的堆底元素不再进行新的调整,直到将倒数第二个元素调整完毕后结束。
所以说堆排序虽说效率较高,但是它的算法步骤却不如其他排序那么明了,需要将它的每一个算法步骤了解清楚后,才能清晰的解析出来。
二、堆排序的算法步骤
在排序家族中,堆排序是一种效率比较高的方法,它的 时间复杂度为O(nlogn),空间复杂度为O(1),它的主要排序步骤为:建堆、交换堆顶、堆底元素再向下调整。
但是在此之前,我们需要先解析出两个分支算法,分别是向下调整和向上调整。
顾名思义,向上(下)调整分别是从堆底(顶)为起始向堆顶(底)进行调整,目的则是严格维护堆的结构不被破坏。
在本文的演示中,我们暂且以大根堆为例。
2.1向下调整
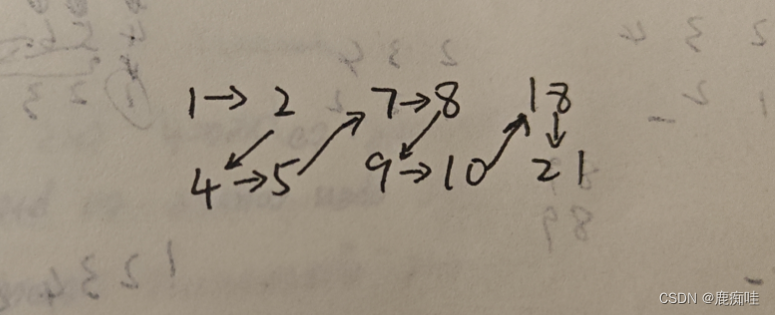
首先,我们以【2,6,3,0,7】为例进行演示。
我们先按照顺序构建堆,如下所示:
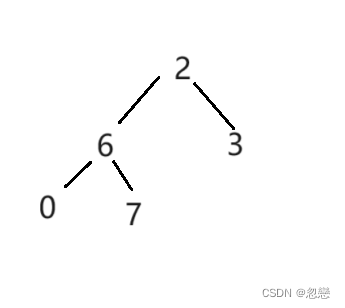
然后我们建立两个int类型的变量parent和child,分别指向2和它的子节点,这里子节点的公式为(parent*2+1)。
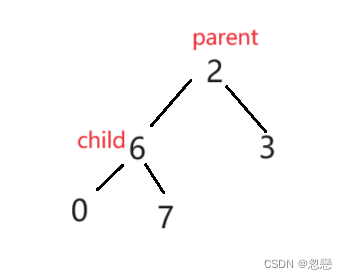
接下来就是要将parent所指的元素和child所指的元素进行比较,如果parent所指元素小于child所指元素则进行交换,再更新两个变量的位置,如果child所指元素不大于parent所指元素,则跳出循环。
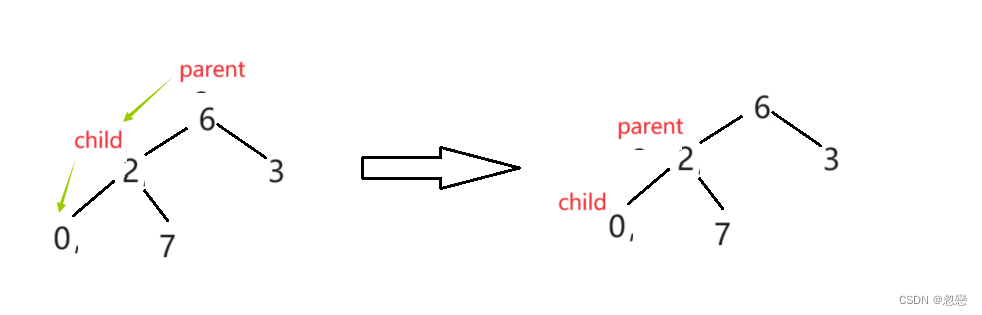
这样,一趟的向下调整就完成了,下面我们用代码实现:
//向下调整
void Modify_down(int parent , int end)
{
int child = parent * 2 + 1;
while (child <= end)
{
if (child + 1 < end && _v[child] < _v[child + 1])
{
child++;
}
if (_v[child] > _v[parent])
{
swap(_v[parent], _v[child]);
parent = child;
child = child * 2 + 1;
}
else
break;
}
}2.2向上调整
向上调整和向下调整有所不同,需要先找出其孩子节点中最大的那个,比较之后再进行交换操作,以【2,6,7,0,3】为例。
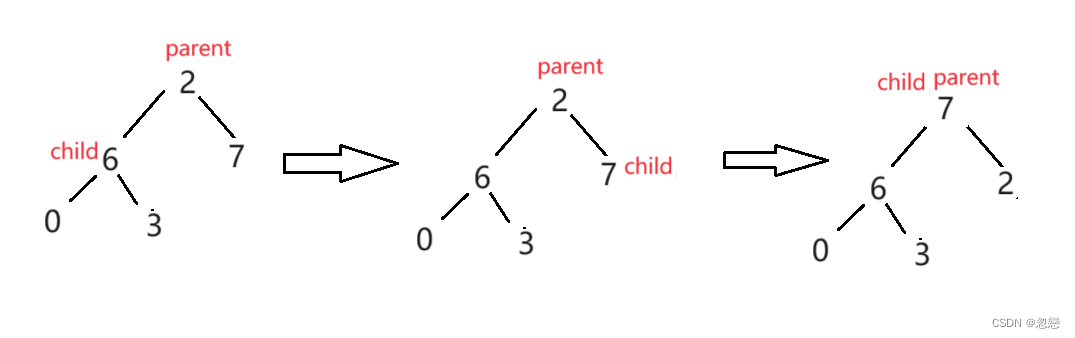
调整过程中,计算父节点的计算方法为【(child-1)/2】,然后比较兄弟节点,找出最大的那个,如果孩子节点大于父节点,就进行交换,然后更换parent和child的下标位置,如果子节点小于父节点就跳出循环。代码如下:
//向上调整
void Modify_up(int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (_v[child] > _v[parent])
{
swap(_v[parent], _v[child]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}2.3堆排序
完成两个核心的算法后,我们最后只需将堆排序归纳一下即可。
1、建堆,将堆调整至合法。
//向上调整
void Modify_up(int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (_v[child] > _v[parent])
{
swap(_v[parent], _v[child]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
//建堆
for (int i = 1; i < _v.size(); i++)
{
Modify_up(i);
}2、交换堆顶和堆底元素,然后再进行向下调整堆,在这里对于堆底的下标我们以变量“end”来控制,当end<=0时,则跳出循环。
//向下调整
void Modify_down(int parent , int end)
{
int child = parent * 2 + 1;
while (child <= end)
{
if (child + 1 < end && _v[child] < _v[child + 1])
{
child++;
}
if (_v[child] > _v[parent])
{
swap(_v[parent], _v[child]);
parent = child;
child = child * 2 + 1;
}
else
break;
}
}
int end = _v.size() - 1;
while (end > 0)
{
swap(_v[0], _v[end]);
end--;
Modify_down(0, end);
}三、堆排序完整代码
class heapsort
{
public:
heapsort(vector<int>& v)
:_v(v)
{}
void heap_sort()
{
for (int i = 1; i < _v.size(); i++)
{
Modify_up(i);
}
int end = _v.size() - 1;
while (end > 0)
{
swap(_v[0], _v[end]);
end--;
Modify_down(0, end);
}
}
void Print()
{
for (int i = 0; i < _v.size(); i++)
{
cout << _v[i] << " ";
}
}
protected:
//向上调整
void Modify_up(int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (_v[child] > _v[parent])
{
swap(_v[parent], _v[child]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
//向下调整
void Modify_down(int parent , int end)
{
int child = parent * 2 + 1;
while (child <= end)
{
if (child + 1 < end && _v[child] < _v[child + 1])
{
child++;
}
if (_v[child] > _v[parent])
{
swap(_v[parent], _v[child]);
parent = child;
child = child * 2 + 1;
}
else
break;
}
}
private:
vector<int> _v;
};四、、堆排序的适用场景
堆排序适用于关键字较多的情况,如:在几亿个关键字中找出前十个最大的数据,我们只需建立小根堆,然后依次循环十次就能得到想要的数据了。