Dynamic Programming

动态规划（Dynamic Programming, DP） 是一种算法设计技巧，通常用来解决具有重叠子问题和最优子结构性质的问题。它通过将问题分解为更小的子问题，逐步解决这些子问题并将结果存储起来，以避免重复计算，从而提高效率。

---

1. 特点

1.1 重叠子问题

在许多递归问题中，计算过程中会多次遇到相同的子问题。如果我们每次遇到这些子问题时都重新计算，会导致大量的重复计算和效率低下。重叠子问题的思想是通过将子问题的结果存储起来，避免重复计算，从而提高效率。

举例

斐波那契数列

递归关系式

$$T(n)=T(n-1)+T(n-2)$$

计算T(3)

$$\begin{array}{rl}T(3)& =T(2)+T(1)\\ & =T(1)+T(0)+T(1)\end{array}$$

这里我们可以看见T(1)被多次计算

这个多次计算的T(1)便被称为重复子问题

如果我们用递归来解决这个问题

int fin(int n){
    if(n==1)return 1;
    if(n==0)return 0;
    return fin(n-1)+fin(n-2);
}

画出递归树

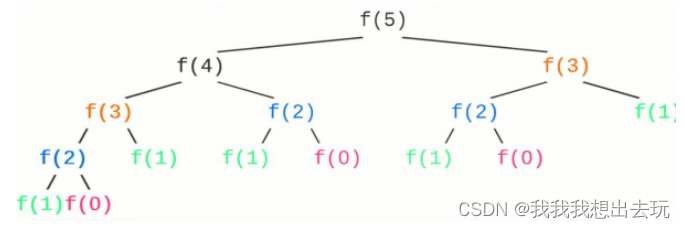
我们可以看到有多次递归调用都是重复的，即出现了重复子问题。

1.2 记忆化存储

继续探究斐波那契问题

我们之前发现使用递归解决问题时出现了多次递归调用是重复的

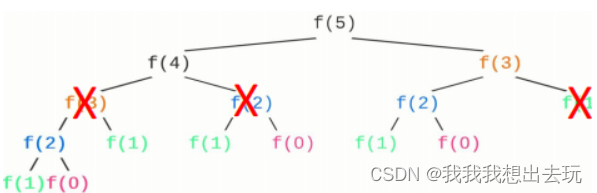
我们可以将这些重复子问题的结果储存起来,这样下一次需要解决这个子问题的时候，只需要访问之前的结果就可以了。

模拟实现

int fin(int n){
    std::vector<int>Fin(n+1);
    Fin[0]=0;
    Fin[1]=1;
    for(int i=2;i<=n;i++){
        Fin[i]=Fin[i-1]+Fin[i-2];
    }
    return Fin[n];
}

可以看出来我们是从最小子问题来逐渐递推至最后的答案，这也被称为自底而上的算法

1.4 状态转移方程

我们来看斐波那契数列的递推关系式

$$T(n)=T(n-1)+T(n-2)$$

这里我们可以看出，如果我们想得到第n项的答案，我们就要知道第n-1项和第n-2项的答案

$$T(n)\leftarrow 这个第n项的答案，就定义为一个状态$$

状态转移方程表示的就是某一个状态和其他状态之间的关系

$$T(n)=T(n-1)+T(n-2)$$

这个方程就表示第n个状态是由第n-1个状态和第n-2个状态决定

1.5 最优子结构

还是看斐波那契数列

我们如果要求出第n个状态的状态值，那么我们一定是使用第n-1个状态和第n-2个状态的值来计算的。

由于我们的状态转移方程是确定的，这里求出的一定是最优解。

给出定义

如果一个问题的最优解包含了其子问题的最优解，则称这个问题具有最优子结构性质。

---

2. 用动态规划来设计算法的步骤

2.1 理解问题并确定子问题

首先，理解斐波那契数列的问题。斐波那契数列定义如下：

$$F(n)=F(n-1)+F(n-2)$$

其初始条件为：
$$F(0)=0$$
$$F(1)=1$$

这个问题可以分解为子问题，即计算第 ( n ) 项的值依赖于第 ( n-1 ) 项和第 ( n-2 ) 项的值。

2.2 定义状态

定义状态 ( dp[i] ) 表示斐波那契数列第 ( i ) 项的值。

$$dp[i]\leftarrow 斐波那契数列第i项的值$$

2.3 确定状态转移方程

状态转移方程基于斐波那契数列的递归定义，可以写作：
$$dp[i]=dp[i-1]+dp[i-2]$$

2.4 确定初始状态和边界

根据斐波那契数列的初始条件，初始化状态：

$$dp[0]=0$$
$$dp[1]=1$$

2.5 利用状态转移方程计算状态值

使用状态转移方程从初始状态开始逐步计算到目标状态值。

#include <vector>

int fib(int n) {
    if (n <= 1) return n;
    std::vector<int> dp(n + 1);
    dp[0] = 0;
    dp[1] = 1;
    for (int i = 2; i <= n; ++i) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}