本篇文章是博主在人工智能等领域学习时,用于个人学习、研究或者欣赏使用,并基于博主对人工智能等领域的一些理解而记录的学习摘录和笔记,若有不当和侵权之处,指出后将会立即改正,还望谅解。文章分类在AI学习笔记:
AI学习笔记(9)---《分类判决界面---W-H、H-K算法》
分类判决界面---W-H、H-K算法
目录
一、算法原理
1.1 W-H算法
1.2 H-K算法
二、实验要求
三、实验流程
四、运行结果
一、算法原理
1.1 W-H算法
对于两类问题,设n+1维增广训练模式x1, x2, ...,xN已符号规范化。如果训练模式是线性可分的,则存在权矢量w使不等式组
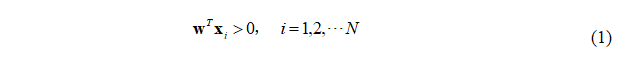
成立,即不等式组是一致的,有解。若训练模式是非线性可分的,表明不存在权矢量w对所有的训练模式都能正确分类,也就是说,无论任何的权矢量w,都有某些模式被错分,不等式不能都成立,即不等式组是不一致的,不等式组无解。在这种情况下,我们希望所求得的权矢量使尽可能多的不等式被满足,等价地说,使最少的训练模式被错分,或所得界面较稳健使对待分类模式有较好的分类效果。
将上面的不等式组写成矩阵方程形式,为使解可靠,引人N维余量矢量b>0,于是不等式方程组变为

1.2 H-K算法

其他分类判决界面方法见
分类判决界面---W-H、H-K算法
二、实验要求
采用下列两类模式为样本:
w1 = [0 0 0; 1 0 0; 1 0 1; 1 1 0]
w2 = [0 0 1; 0 1 1; 0 1 0; 1 1 1; 1 -1 0]
编程实现W-H算法和HK算法,对任意输入新样本进行分类判别。
三、实验流程
3.1 W-H 算法matlab代码
新建main.m文件
clc;
close all;
%% 数据预处理
X1 = [0 0 0; 1 0 0; 1 0 1; 1 1 0];
X2 = [0 0 1; 0 1 1; 0 1 0; 1 1 1; 1 -1 0];
X = [X1;-X2];
[N1,W] = size(X);
b = ones(N1,1);
%b = [9; 3; 1; 9; 1; 4; 2; 1];
%% W-H 算法
rou1 =1;
k1 = 100;
%w = zeros(W,1);
w = ones(W,1);
[w1, a1] = W_H(X,w,b,rou1,k1);
disp("解矢量:");
disp(w1);
disp("迭代次数:");
disp(a1);
% 画图
figure()
x1=X1(:,1);
y1=X1(:,2);
z1=X1(:,3);
scatter3(x1,y1,z1,'k'); %圆圈为正样本
hold on;
x2=X2(:,1);
y2=X2(:,2);
z2=X2(:,3);
scatter3(x2,y2,z2,'P'); %五角星为负样本
hold on;
x3 = w1(1);
y3 = w1(2);
z3 = w1(3);
[X,Y] = meshgrid(-2:2:2); %以法线绘制平面
Z = -(x3 * X + y3 * Y) / z3;
mesh(X,Y,Z,'FaceAlpha', '0.8');
xlabel('x'),ylabel('y'),zlabel('z');
title('W-H算法分类判决界面');新建W_H.m文件
function [w,a] = W_H(X,w,b,rou,k)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% X:符号化的训练样本
% b:余量(初值设置为大于零的较小的值)
% rou:参数(设为0.5)
% k:迭代次数
% w:解矢量
% a:算法结束时的迭代次数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
N = size(X,1); % 样本数量
X = X';
a = 0;
while a < k % 最大迭代次数
a = a + 1;
old_w = w;
for i = 1:N
w = w + (rou/i)*(b(i) - w'*X(:,i))*X(:,i); % 迭代w的值
end
if norm(w - old_w) < 0.0001 % 求向量范数,如果收敛了就提前结束
break
end
end
end3.2 H-K 算法matlab代码
main.m文件下面补充
%% H-K 算法
X = [X1;-X2];
[N1,W] = size(X);
b = ones(N1,1);
%b = [9; 3; 1; 9; 1; 4; 2; 1];
rou2 = 0.5;
[w2, a2] = H_K(X,b,rou2);
disp("解矢量:");
disp(w2);
disp("迭代次数:");
disp(a2);
% 画图
figure()
x1=X1(:,1);y1=X1(:,2);z1=X1(:,3);
scatter3(x1,y1,z1,'o'); % 圆圈为正样本
hold on;
x2=X2(:,1);y2=X2(:,2);z2=X2(:,3);
scatter3(x2,y2,z2,'P'); % 五角星为负样本
hold on;
x3 = w2(1);y3 = w2(2);z3 = w2(3);
[X,Y] = meshgrid(-2:2:2); % 以法线绘制平面
Z = -(x3 * X + y3 * Y) / z3;
mesh(X,Y,Z,'FaceAlpha', '0.8');
xlabel('x'),ylabel('y'),zlabel('z');
hold on
title('H-K算法分类判决界面');新建H_K.m文件
function [w , a] = H_K(X,b,rou)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% X:符号化的训练样本
% b:余量(初值设置为大于零的较小的值)
% rou:参数(设为0.5)
% k:迭代次数
% w:解矢量
% a:算法结束时的迭代次数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
XX = inv(X'*X)*X'; % 求符号化的训练样本的伪逆矩阵
a = 0;
while 1 % 循环开始
a = a + 1;
w = XX*b; % 求w值
e = X*w - b; % 计算误差矢量
if sum(abs(e) >= 0.001) == 0 % 如果e为零矢量,则算法停止,此时判定为0的标准为0.001
break
elseif sum(abs(e > 0)) == 0 % 如果e没有正分量的非零矢量,或负的分量停止变为正值,则算法停止
break
else
b = b + rou*(e + abs(e)); % 迭代b
w = XX*b; % 迭代w
end
end
end四、运行结果
4.1 W-K 算法运行结果
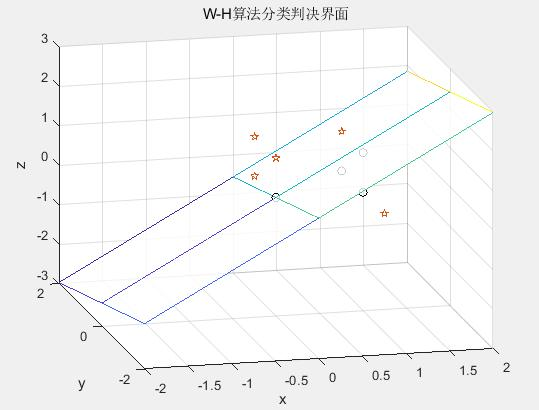

4.2 H-K 算法运行结果
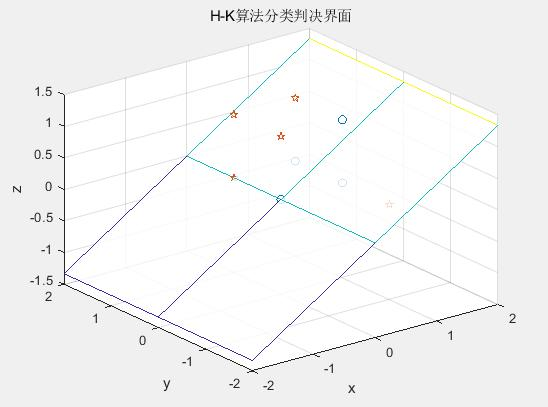

文章若有不当和不正确之处,还望理解与指出。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请联系博主删除。如有错误、疑问和侵权,欢迎评论留言联系作者,或者私信联系作者。