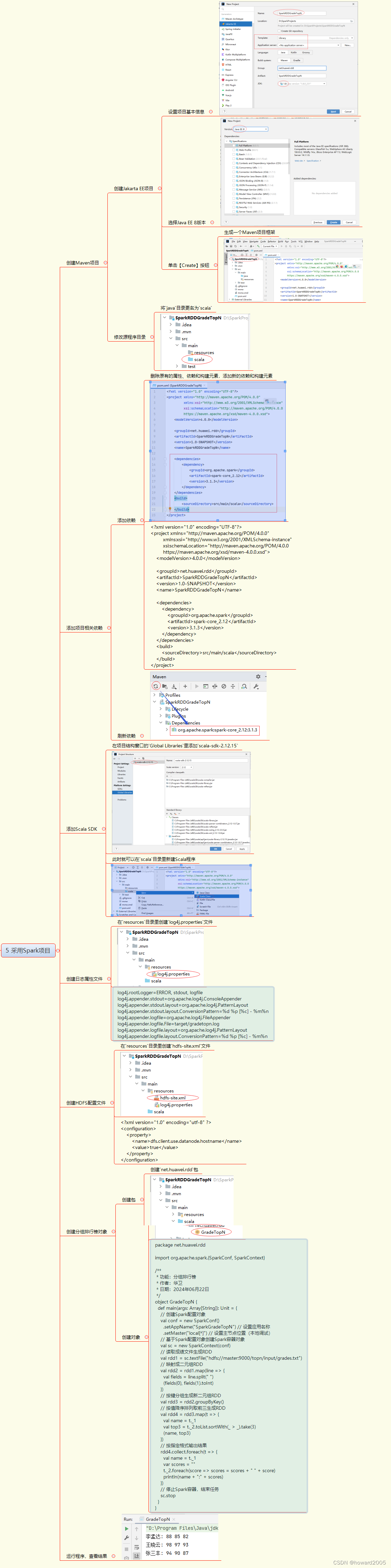
前言

本文还是作为前置知识。

LTI系统的传递函数

LTI系统的传递函数 $H(z)$ 是输出信号的z变换 $Y(z)$ 与输入信号的z变换 $X(z)$ 的比值：

$H(z)=\frac{Y(z)}{X(z)}$

多项式比值表示

传递函数 $H(z)$ 通常表示为两个多项式的比值形式：

$H(z)=\frac{B(z)}{A(z)}$

其中：

• $B(z)$ 是输入信号的多项式，表示系统的零点（零点多项式）。
• $A(z)$ 是输出信号的多项式，表示系统的极点（极点多项式）。

具体来说，$B(z)$ 和 $A(z)$ 可以表示为：

$B(z)=b_0+b_1{z}^{-1}+b_2{z}^{-2}+\cdots +b_M{z}^{-M}$

$A(z)=1+a_1{z}^{-1}+a_2{z}^{-2}+\cdots +a_N{z}^{-N}$

因此，传递函数可以表示为：

$H(z)=\frac{b_0+b_1{z}^{-1}+b_2{z}^{-2}+\cdots +b_M{z}^{-M}}{1+a_1{z}^{-1}+a_2{z}^{-2}+\cdots +a_N{z}^{-N}}$

差分方程表示

对应的差分方程为：

$y[n]+a_{1}y[n-1]+a_{2}y[n-2]+\cdots +a_{N}y[n-N]=b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]+\cdots +b_{M}x[n-M]$

示例

假设我们有一个系统，其传递函数为：

$H(z)=\frac{1+0.5z^{-1}}{1-0.5z^{-1}}$

对应的多项式为：

$B(z)=1+0.5z^{-1}$

$A(z)=1-0.5z^{-1}$

对应的差分方程为：

$y[n]-0.5y[n-1]=x[n]+0.5x[n-1]$

拉普拉斯变换

这个在[信号与系统]有关带有冲激响应和阶跃响应的拉普拉斯变换求解法一文中已经给出了很多有关拉普拉斯的定理和性质，这里简单复述一下

1. 拉普拉斯变换

普拉斯变换可以简化微分方程的求解过程，把微分方程转化为代数方程。公式如下：

F ( s ) = L { f ( t ) } = ∫ 0 ∞ f ( t ) e − s t F(s) = \mathcal{L}\{f(t)\} = \int_{0}^{\infty} f(t) e^{-st} F(s)=L{f(t)}=∫0∞​f(t)e−st

其中s是一个复数变量，这里只当为一个常数即可

2. 有关拉普拉斯变换的几个性质

L { f ( t ) } = F ( s ) {L}\{f(t)\}=F(s) L{f(t)}=F(s)

L { f ′ ( t ) } = s F ( s ) − f ( 0 ) {L}\{f'(t)\} = sF(s) - f(0) L{f′(t)}=sF(s)−f(0)

L { f ′ ′ ( t ) } = s 2 F ( s ) − s f ( 0 ) − f ′ ( 0 ) {L}\{f''(t)\} = s^2 F(s) - sf(0) - f'(0) L{f′′(t)}=s2F(s)−sf(0)−f′(0)

3. 有关单位阶跃函数的拉普拉斯变换：

单位阶跃函数表达式如下：

$\varepsilon (t)=\{\begin{array}{ll}0,& t<0\\ 1,& t\ge 0\end{array}$

我们有 L { ɛ ( t ) } = ∫ 0 ∞ ɛ ( t ) e − s t   d t = 1 s , Re ( s ) > 0 {L}\{ɛ(t)\} = \int_{0}^{\infty} ɛ(t) e^{-st} \, dt = \frac{1}{s}, \quad \text{Re}(s) > 0 L{ɛ(t)}=∫0∞​ɛ(t)e−stdt=s1​,Re(s)>0

由于 $u(t)=1$ ，所以积分变为： L { ɛ ( t ) } = ∫ 0 ∞ e − s t   d t \mathcal{L}\{ɛ(t)\} = \int_{0}^{\infty} e^{-st} \, dt L{ɛ(t)}=∫0∞​e−stdt

计算该积分：

$${\int }_0^{\infty }{e}^{-st}dt={\left[\frac{e^{-st}}{-s}\right]}_0^{\infty }=\left(0-\left(-\frac{1}{s}\right)\right)=\frac{1}{s},\text{Re}(s)>0$$

因此，单位阶跃函数 ɛ(t) 的拉普拉斯变换为：

L { ɛ ( t ) } = 1 s , Re ( s ) > 0 \mathcal{L}\{ɛ(t)\} = \frac{1}{s}, \quad \text{Re}(s) > 0 L{ɛ(t)}=s1​,Re(s)>0

4. 拉普拉斯变换的基本线性性质
L { a f ( t ) + b g ( t ) } = a F ( s ) + b G ( s ) {L}\{af(t) + bg(t)\} = aF(s) + bG(s) L{af(t)+bg(t)}=aF(s)+bG(s)

拉普拉斯变换是描述模拟域的。如果将$\sigma$和$w$分别作为平面坐标系的x轴和y轴，这个平面就是我们定义的s平面。

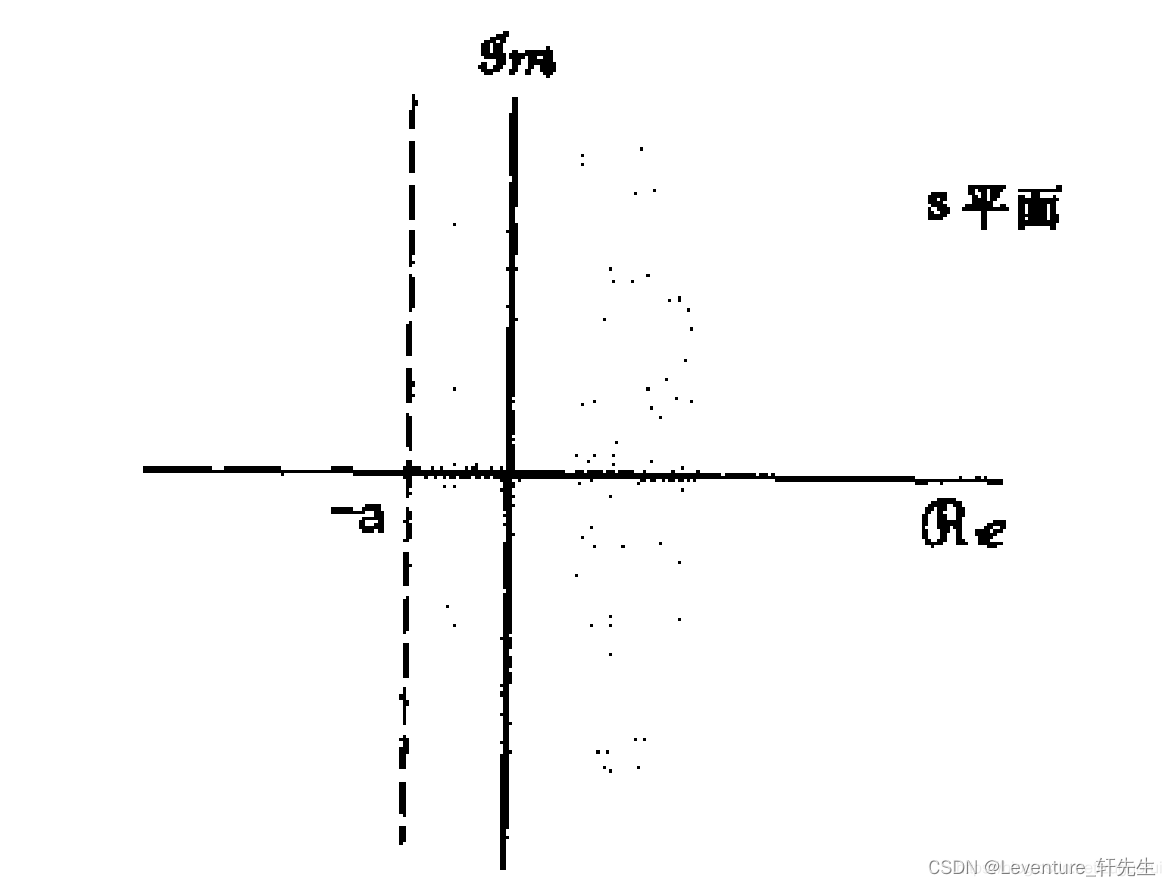
可以看到，拉普拉斯变换实际上就是为将信号幅值增益为原来的$e^{\sigma }$倍。如果$\sigma =0$，则特化为连续信号的傅里叶变换，落在s平面上就是虚轴。

一个信号的拉普拉斯变换是有收敛域的。如果x(t)的拉普拉斯变换是有理的，如果x(t)是右边信号，那么其收敛域ROC就位于s平面上最右边极点的右边。如果x(t)是左边信号，那么其收敛域就位于s平面上最左边极点的左边。 我们实际处理的信号都是有理的且为右边信号，因此适用于第一种情况。

z变换

z变换（z-Transform）是离散时间信号处理中的一种重要工具，用于分析和处理离散时间信号和系统。它是傅里叶变换在离散时间域的扩展，能够将离散时间信号转换到复频域，从而简化信号和系统的分析与设计。

$$X(z)=\sum _{n=-\infty }^{\infty }x[n]z^{-n}$$

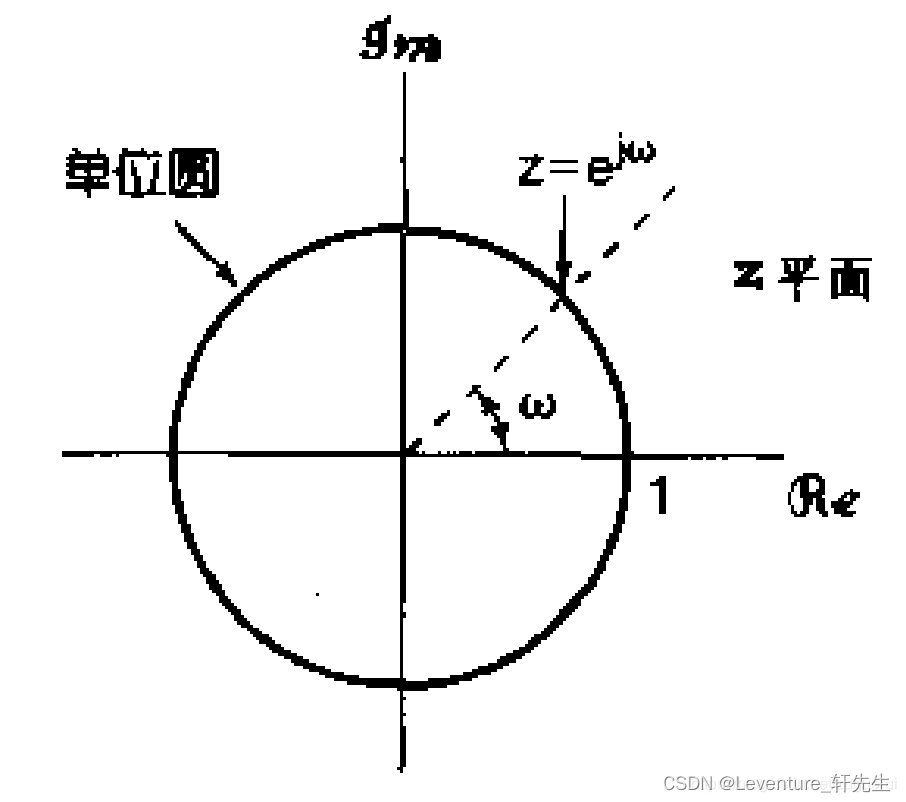
其中，$z=r{e}^{jw}$
若将$r$看作$z$的幅值，w看作z的相角，则两者的关系可以看作一个极坐标表示的平面，称为z平面

其中：

• $X(z)$ 是信号 $x[n]$ 的z变换。
• $z$ 是一个复数变量，通常表示为 $z=r{e}^{j\omega }$，其中 $r$ 是半径， $\omega$ 是角频率。

一些常见信号及其z变换对如下：

1. 单位冲激函数 $\delta [n]$：
   $\delta [n]\leftrightarrow 1$

2. 单位阶跃函数 $u[n]$：
   $u[n]\leftrightarrow \frac{1}{1-z^{-1}}\text{for }|z|>1$

3. 指数序列 $a^{n}u[n]$：
   $a^{n}u[n]\leftrightarrow \frac{1}{1-a{z}^{-1}}\text{for }|z|>|a|$

z变换有许多重要的性质，有助于简化信号和系统的分析：

1. 线性性：
   Z { a x [ n ] + b y [ n ] } = a X ( z ) + b Y ( z ) \mathcal{Z}\{a x[n] + b y[n]\} = a X(z) + b Y(z) Z{ax[n]+by[n]}=aX(z)+bY(z)

2. 时间移位：
   Z { x [ n − k ] } = z − k X ( z ) \mathcal{Z}\{x[n - k]\} = z^{-k} X(z) Z{x[n−k]}=z−kX(z)

3. 时间反转：
   Z { x [ − n ] } = X ( z − 1 ) \mathcal{Z}\{x[-n]\} = X(z^{-1}) Z{x[−n]}=X(z−1)

4. 卷积：
   Z { x [ n ] ∗ h [ n ] } = X ( z ) H ( z ) \mathcal{Z}\{x[n] * h[n]\} = X(z) H(z) Z{x[n]∗h[n]}=X(z)H(z)

5. 微分性质：
   Z { n x [ n ] } = − z d d z X ( z ) \mathcal{Z}\{n x[n]\} = -z \frac{d}{dz} X(z) Z{nx[n]}=−zdzd​X(z)

逆z变换

用于将复频域的z变换恢复为时间域的序列。对于给定的 $X(z)$，其逆z变换定义为：

$x[n]=\frac{1}{2\pi j}{\oint }_{C}X(z)z^{n-1}dz$

其中，积分路径 $C$ 是一条围绕原点的闭合路径，且位于收敛区域内。

举例

下面是一个简单的例子来展示如何计算z变换和逆z变换：

例子：计算序列 $x[n]=0.5^{n}u[n]$ 的z变换

1. z变换计算：
   $X(z)={\sum }_{n=0}^{\infty }(0.5^n)z^{-n}={\sum }_{n=0}^{\infty }{\left(\frac{0.5}{z}\right)}^n=\frac{1}{1-0.5z^{-1}}\text{for }|z|>0.5$

2. 逆z变换验证：
   $x[n]={\mathcal{Z}}^{-1}\left\{\frac{1}{1-0.5z^{-1}}\right\}=0.5^{n}u[n]$

基于Z变换，我们可以将数字域LTI系统的转换方程用两个多项式的比来表示

传递函数的定义

对于一个离散时间LTI系统，其传递函数 $H(z)$ 定义为输出信号的z变换 $Y(z)$ 与输入信号的z变换 $X(z)$ 的比值：

$H(z)=\frac{Y(z)}{X(z)}$

多项式比值表示

在实际应用中，传递函数 $H(z)$ 通常表示为两个多项式的比值：

$H(z)=\frac{B(z)}{A(z)}$

其中：

• $B(z)$ 是输入信号的多项式，表示系统的零点（零点多项式）。
• $A(z)$ 是输出信号的多项式，表示系统的极点（极点多项式）。

具体来说，$B(z)$ 和 $A(z)$ 可以表示为：

$B(z)=b_0+b_1{z}^{-1}+b_2{z}^{-2}+\cdots +b_M{z}^{-M}$

$A(z)=1+a_1{z}^{-1}+a_2{z}^{-2}+\cdots +a_N{z}^{-N}$

因此，传递函数可以表示为：

$H(z)=\frac{b_0+b_1{z}^{-1}+b_2{z}^{-2}+\cdots +b_M{z}^{-M}}{1+a_1{z}^{-1}+a_2{z}^{-2}+\cdots +a_N{z}^{-N}}$

差分方程

对应的差分方程为：

$y[n]+a_{1}y[n-1]+a_{2}y[n-2]+\cdots +a_{N}y[n-N]=b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]+\cdots +b_{M}x[n-M]$

示例

假设我们有一个系统，其传递函数为：

$H(z)=\frac{1+0.5z^{-1}}{1-0.5z^{-1}}$

对应的多项式为：

$B(z)=1+0.5z^{-1}$

$A(z)=1-0.5z^{-1}$

对应的差分方程为：

$y[n]-0.5y[n-1]=x[n]+0.5x[n-1]$