1.求水仙花数

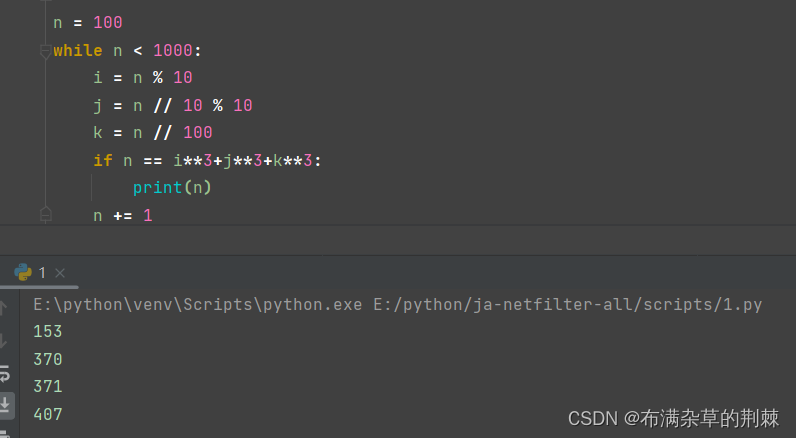
求1000以内的水仙花数。水仙花是指，一个三位数，其各位数字的立方和等于该数本身

n = 100
while n < 1000:
    i = n % 10
    j = n // 10 % 10
    k = n // 100
    if n == i**3+j**3+k**3:
        print(n)
    n += 1

2.求兔子数 

有一对兔子，从第三个月开始生一对兔子，小兔子长到第三个月也生一对兔子，假如兔子不死，第二十一个月有多少对兔子

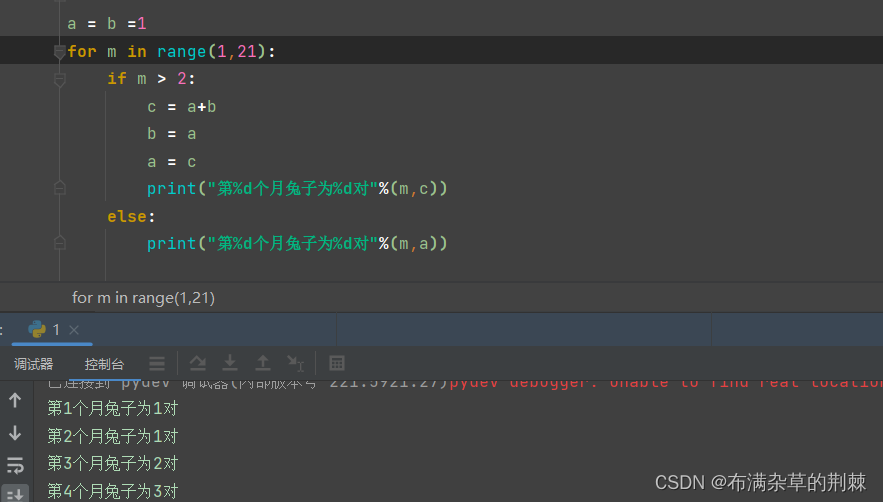
第一个月兔子数  1
第二个月兔子数  1
第三个月兔子数= 1+1
第四个月兔子数= 1+1+1
第五个月兔子数= 1+1+1+1+1
第五个月兔子数= 1+1+1+1+1+1+1+1

a = b =1
for m in range(1,21):
    if m > 2:
        c = a+b
        b = a
        a = c
        print("第%d个月兔子为%d对"%(m,c))
    else:
        print("第%d个月兔子为%d对"%(m,a))

 3.抓小偷

警察抓了四名嫌疑犯，其中一个是小偷，审讯口供如下：

a说：我不是小偷

b说：c是小偷

c说：小偷肯定是d

d说：c胡说

已知三人说的是实话，一人说的是假话，编写程序推断谁是小偷

l = "abcd"
for i in l:
    #三个为真一个为假结果为三
    if (i!="a")+(i=="c")+(i=="d")+(i!="d")==3:
        print(i+"是小偷")

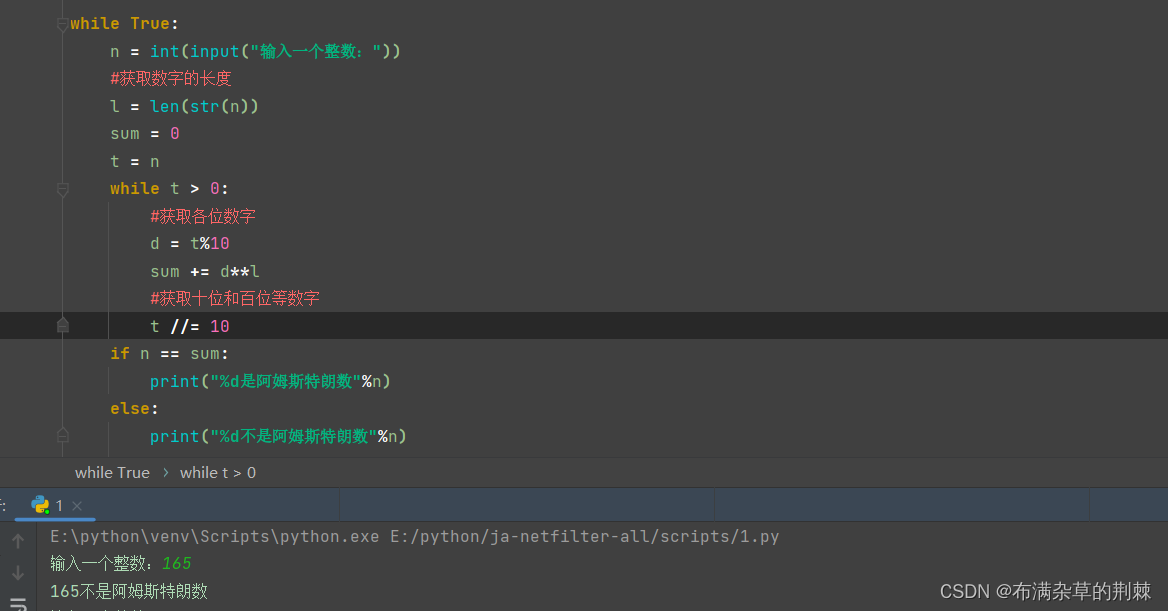
4.求阿姆斯特朗数

一个n位的正整数等于他各位数字的n次方之和，当n为 3时称为水仙花数。

while True:
    n = int(input("输入一个整数："))
    #获取数字的长度
    l = len(str(n))
    sum = 0
    t = n
    while t > 0:
        #获取各位数字
        d = t%10
        sum += d**l
        #获取十位和百位等数字
        t //= 10
    if n == sum:
        print("%d是阿姆斯特朗数"%n)
    else:
        print("%d不是阿姆斯特朗数"%n)

5.数字组合游戏

 有1234四个数字组成每位不同的三位数

for i in range(1,5):
    for j in range(1,5):
        for k in range(1,5):
            if (i!=j) and (i!=k) and (j!=k):
                print(i*100+j*10+k,end=" ")

 6.反弹运动

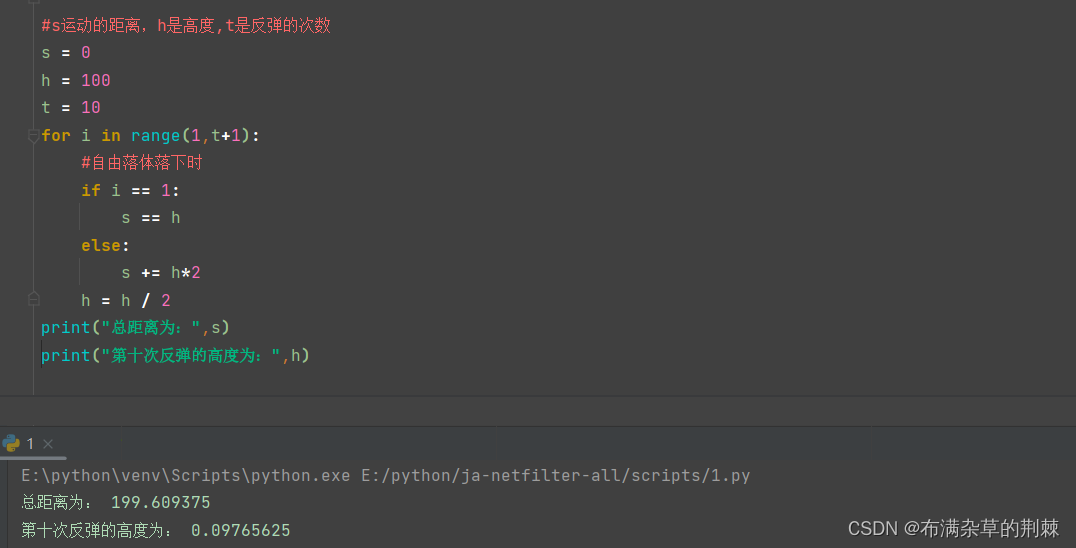
假设有一只小球，从一百米高空自由落下，每次落地后反跳回原高度的一半在落下，当小球第十次反弹时，共运行了多少米，求第十次反弹的高度

第一次高度100

第一次反弹 50+50

第二次反弹 25+25

第三次反弹 12.5+12.5

。。。。。

#s运动的距离，h是高度,t是反弹的次数
s = 0
h = 100
t = 10
for i in range(1,t+1):
    #自由落体落下时
    if i == 1:
        s == h
    else:
        #反弹时的距离为上一次的一半
        s += h*2
    h = h / 2
print("总距离为：",s)
print("第十次反弹的高度为：",h)

7.拿鸡蛋问题

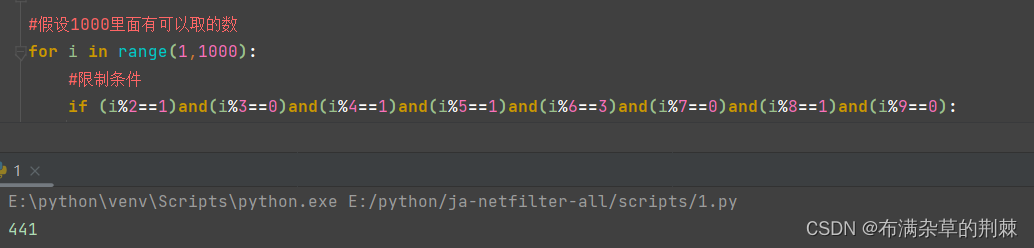
 假设一筐鸡蛋，如果一个一个拿，正好拿完。如果两个俩个拿，还剩一个。如果三个三个拿，正好拿完。如果四个四个拿，还剩一个。如果五个五个拿，还差一个。如果六个六个拿，还剩三个。如果七个七个拿，正好拿完。如果八个八个拿，还剩一个。如果九个九个拿，正好拿完，问这筐鸡蛋至少有多少个。

#假设1000里面有可以取的数
for i in range(1,1000):
    #限制条件
    if (i%2==1)and(i%3==0)and(i%4==1)and(i%5==1)and(i%6==3)and(i%7==0)and(i%8==1)and(i%9==0):