目录
一、实验目的
二、问题描述
三、实验要求
四、算法思想和实验结果
1、动态规划法原理:
2、解决方法:
2.1 方法一:常规动态规划
2.1.1 算法思想:
2.1.2 时间复杂度分析
2.1.3 时间效率分析
2.2 方法二:动态规划加二分查找最优x
2.2.1 算法思想:
2.2.2 时间复杂度分析
2.2.3 时间效率分析
2.3 方法三:动态规划加逆向求解
2.3.1 算法思想
2.3.2 时间复杂度分析
2.3.3 时间效率分析
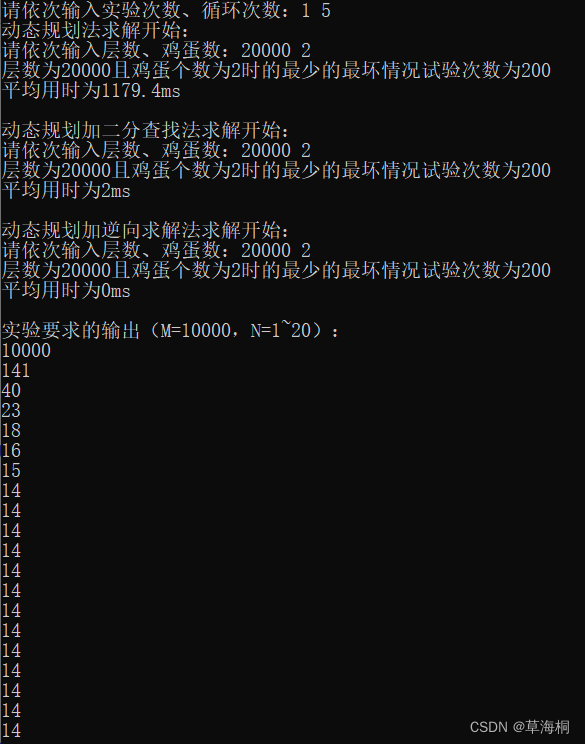
3、结果输出示例
一、实验目的
1. 掌握动态规划算法设计思想。
2. 掌握扔鸡蛋问题的动态规划法。
二、问题描述
扔鸡蛋问题是计算机程序设计中的一个经典问题。从一幢楼房的不同楼层往下扔鸡蛋,用最少的最坏情况试验次数,确定鸡蛋不会摔碎的最高安全楼层。仅有一个鸡蛋供试验时,只能采用顺序查找法。有足够多的鸡蛋时,可以采用二分查找法。有多于一个但数量有限的鸡蛋时,采用动态规划方法求解。双蛋问题(two-egg problem)是本问题的一个特例,曾出现于谷歌的程序员面试题中。
有一幢楼房高层。某人准备了N个鸡蛋供试验。他想知道鸡蛋从几层扔下不会摔碎,并确定出最高安全楼层。试验过程中,鸡蛋没有摔碎则可以继续使用,摔碎了则需要换一个鸡蛋继续试验。为保证试验成功,此人要设计一个程序,以最小化最坏情况的试验次数F(M, N)。作为一个数学抽象,本问题采用一些理想化假设:所有鸡蛋抗摔能力相同,不计重复坠地的累积损伤,且忽略试验结果的偶然性。试验成功的标准是在N个鸡蛋用完之前,精确确定最高安全楼层是哪一层。允许有鸡蛋剩余。
如果只有N=1个鸡蛋供试验,则为了保证试验成功,只能从一层开始逐层往上试验。这相当于采用顺序查找算法,最坏试验次数F(M, 1)=M。如果一层就碎了,则最高安全楼层为0。如果M层还不碎,则最高安全楼层为M。
三、实验要求
1. 给出解决问题的动态规划方程;
2. 理论分析该算法的时间复杂度;
3. 分别测试M=10000, 20000, …, 100000, N=20时以及M=50000, N=11, 12, …, 20时的算法运行时间,并分析实验结果;
4. 依次在终端输出M=10000, N=1~20时的F(M, N)值,实验课时检查该代码,限用C或C++语言编写。
四、算法思想和实验结果
1、动态规划法原理:
将复杂问题划分为更小的子问题,通过子问题的最优解来重构原问题的最优解。求解过程中,保存子问题的解,以便在需要时直接查表而不是重复计算,从而减少计算量。
2、解决方法:
2.1 方法一:常规动态规划
2.1.1 算法思想:
用二维数组k[m][n]表示从第m层扔n个鸡蛋的动态规划法最优解,即该实验所要求的最少的最坏情况试验次数。
对于m层、n个鸡蛋的求解,当尝试从第x层扔下一个鸡蛋时,有两种情况:
1)鸡蛋破碎,剩余n-1个鸡蛋,则在第1层至第x-1层(共x-1层)继续尝试,即k[x-1][n-1]。
2)鸡蛋未破碎,仍剩余n个鸡蛋,则在第x+1至m层(共m-x层)继续尝试,即k[m-x][n];
因为题目要求是最坏情况,所以应该取上述两种情况的较大者。又由于要最少实验次数,所以x应该取让前面的较大者尽量小些的值。
得动态规划方程如下:
k[m][n]=1+min{max{k[x-1][n-1],k[m-x][n]}}(x=1,2,3……,m)
实验时
1)对于m=0、m=1或n=1的情况取值依次为0、1、m(在创建**k时就赋值完成)。
2)对于其他值,用三层for循环自底向上依次确定k[i][j]的值。伪代码如下:
F1(m,n)
for i=2 to m
for j=2 to n
for x=1 to i
k[i][j]=1+max{k[x-1][j-1],k[i-x][j]}
return k[m][n]2.1.2 时间复杂度分析
由前面伪代码可知,最外层m-1次,中间层n-1次,最里层i(i=2,3,……,m)次,则时间复杂度为O(n*m^2)。
2.1.3 时间效率分析
由于效率较低,这里降低数据规模,分别测试M=1000, 2000, …, 10000, N=20时以及M=10000,N=11, 12, …, 20时的算法运行时间(对每种情况都运行5次取平均值)。
1)N=20时,以M=1000为基准
| M | 1000 | 2000 | 3000 | 4000 | 5000 | 6000 | 7000 | 8000 | 9000 | 10000 |
| 平均运行时间/ms | 47 | 190 | 434 | 814 | 1310 | 1964 | 2750 | 3706.2 | 4722.4 | 5802 |
| 理论时间/ms | 47 | 188 | 423 | 752 | 1175 | 1692 | 2303 | 3008 | 3807 | 4700 |
得下图:N=20时的实际效率曲线和理论效率曲线图。

两条曲线一开始较贴合,但随着M的增大,实际运行时间与理论运行时间的差(非负)呈现递增趋势。
2)M等于10000时,以N=11为基准:
| N | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 平均运行时间/ms | 2890.5 | 3152.25 | 3443 | 3832 | 4092.5 | 4408 | 4704 | 5180 | 5478 | 5825 |
| 理论时间/ms | 2890.5 | 3153.27 | 3416.05 | 3678.82 | 3941.59 | 4204.36 | 4467.17 | 4729.91 | 4992.68 | 5255.45 |
得下图:M=10000时的实际效率曲线和理论效率曲线图。

与上一个图一样,两条曲线一开始较贴合,但随着N的增大,实际运行时间与理论运行时间的差(非负)呈现递增趋势。
可能原因是
k[i][j]=1+max{k[x-1][j-1],k[i-x][j]}中的数据访问的耗时实际是随着规模的增大而增大的,但分析时间复杂度和理论时间时忽略这个。(实际效率与理论效率之间差某些常数因子)
2.2 方法二:动态规划加二分查找最优x
2.2.1 算法思想:
对于
for x=1 to m
k[i][j]=1+max{k[x-1][j-1],k[i-x][j]}当x增大时,k[x-1][j-1]是x相关的非递减函数,而k[i-x][j]是x相关的非递增函数。所以可以在前面的基础上,用二分法求出最优的x,而不是从1到m逐个的尝试、比较。
由于层数为整数,二分到最后有两种情况:
1)二分到最后low!=high,如下图,则应该取点1和点3中次数较小的那个(最坏情况下的最少测试次数),即
k[i][j]=min{k[i-low][j],k[high-1][j-1]}

2)分到最后刚好low=high,如下图:此时x=low=high,k[x-1][j-1=,k[i-x][j]。

伪代码如下:
F2(m,n)
for i=2 to m
for j=2 to n
l=1;
h=i;
while l+1<h
x=(l+h)/2
if k[x-1][j-1]<k[i-x][j]
l=x
else if k[x-1][j-1]>k[i-x][j]
h=x
else low=high=x
k=1+min{k[i-l][j],k[h-1][j-1]}
return k[m][n]2.2.2 时间复杂度分析
原来求最优x需m次循环,现在为log m,所以时间复杂度变为O(n*m*log m)
2.2.3 时间效率分析
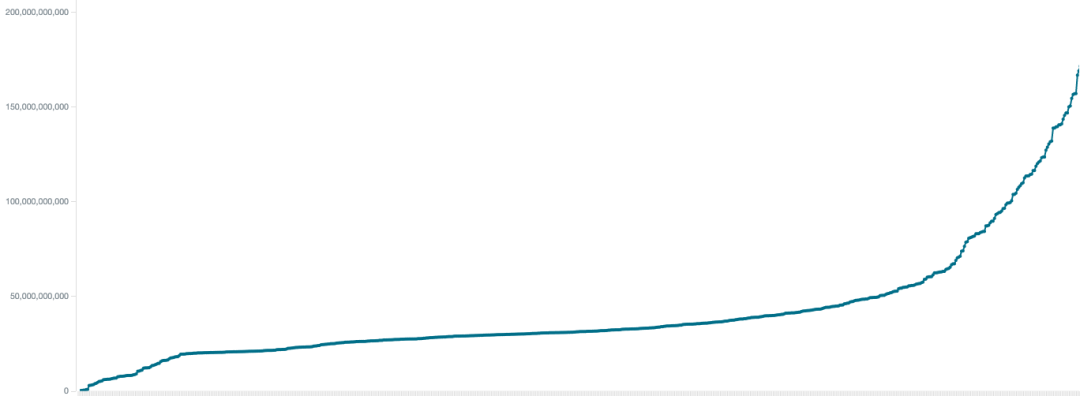
分别测试M=10000, 20000, …, 100000, N=20时以及M=50000, N=11, 12, …, 20时的算法运行时间(对每种情况都运行20次取平均值)。
1)N=20时,以M=10000为基准
| M | 10000 | 20000 | 30000 | 40000 | 50000 | 60000 | 70000 | 80000 | 90000 | 100000 |
| 平均运行时间/ms | 5 | 9.5 | 14.5 | 19.05 | 29.95 | 34.45 | 41.5 | 47.45 | 57.5 | 62.93 |
| 理论时间/ms | 5 | 10.75 | 16.79 | 23.01 | 29.37 | 35.84 | 42.39 | 49.03 | 55.74 | 62.5 |
得下图:N=20时的实际效率曲线和理论效率曲线图。

两条曲线贴合度较高,说明算法效率基本符合关于m的mlog m级关系。
2)M等于50000时,以N=11为基准
| N | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 平均运行时间/ms | 17 | 18.5 | 19.45 | 20 | 22.5 | 24 | 26.25 | 27.25 | 28.25 | 29 |
| 理论时间/ms | 17 | 18.55 | 20.09 | 21.64 | 23.18 | 24.73 | 26.27 | 27.83 | 29.36 | 30.91 |
得下图:M=50000时的实际效率曲线和理论效率曲线图。

两条曲线较贴合,说明算法效率基本符合关于N的线性关系。
2.3 方法三:动态规划加逆向求解
2.3.1 算法思想
不直接按照在m层、n个鸡蛋的情况下求解最少的最坏情况试验次数,而是逆向求解在n个鸡蛋、r次试验次数且最坏情况下最多能测多少层。找到层数大于m时的最小r。
此时扔鸡蛋,碎了,就继续测楼下;没碎,就继续测楼上。
总的可测楼层数 = 楼上的可测楼层数 + 楼下的可测楼层数 + 1(当前这层楼)。即
k[n][r]=k[n][r-1]+k[n-1][r-1]+1
此时的**k和前面的两种方法的不同,分配的空间不再是k[m+1][n+1],而是为k[n][max],max为一个较大的值(由于实验要求的最大规模M=100000、N=20的解为447,所以这里max取1000,实际未知该解时应取更大些)。
伪代码如下:
F3(m,n)
r=0
while k[n][r]<m //r不超过m
r++
for i=1 to n
k[i][r]=k[i][r-1]+k[i-1][r-1]+1
return r2.3.2 时间复杂度分析
外层while循环(不大于)m次,内层for循环n次,所以时间复杂度为O(n*m)。
2.3.3 时间效率分析
效率较高,m=2000000000,n=20时运行时间仍然小于1ms。
3、结果输出示例