高精度乘法的实现

news2024/11/27 2:36:49

这是C++算法基础-基础算法专栏的第九篇文章，专栏详情请见此处。

引入

上次我们学习了高精度加法的实现，这次我们要学习高精度减法的实现。

高精度乘法与高精度加法的定义、前置过程都是大致相同的，如果想了解具体内容，可以移步至我的这篇博客：高精度加法计算的实现。

在这里就不再详细讲解，只讲解主体过程qwq

这里需要说明，此博客（包括后面一篇），都是实现两个高精度数之间的计算，而算法基础课中仅仅实现了一个高精度数和一个低精度数之间的计算，思路和代码上两者有所不同。

主体过程

呃，高精度乘高精度先等会儿，我们先看一种简单的情况。

高精度乘低精度

高精度乘低精度的原理和小学学习的竖式乘法是一样的。

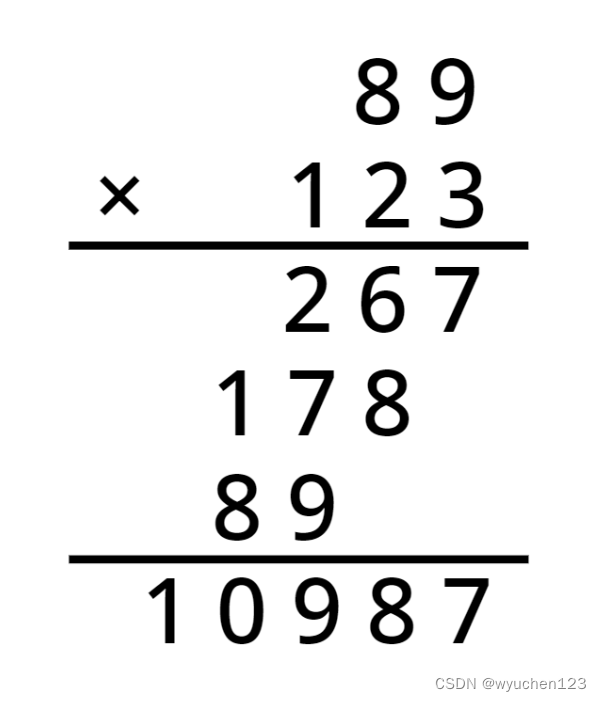
概括来说，从个位开始，将低精度乘数与高精度乘数的每一位相乘，存进积的对应位置上，若当前位达到 $10$ ，进位，也就是将下一位加上当前位（整）除以 $10$ ，并把当前位模 $10$ 。

$89\times 123$ 用高精度计算（ $123$ 为高精度乘数， $89$ 为低精度乘数），先乘个位， $3\times 89$ 得 $267$ ，发现 $267$ 大于等于 $10$ ，所以将 $267$ （整）除以 $10$ ，得 $26$ ，将其存入答案的十位，再将 $267$ 模 $10$ ，得 $7$ ，将其存入答案的个位；

再乘十位， $2\times 89+26$ 得 $204$ ，发现 $204$ 大于等于 $10$ ，所以将 $204$ （整）除以 $10$ ，得 $20$ ，将其存入答案的百位，再将 $204$ 模 $10$ ，得 $4$ ，将其存入答案的十位；

再乘百位， $1\times 89+20$ 得 $109$ ，发现 $109$ 大于等于 $10$ ，所以将 $109$ （整）除以 $10$ ，得 $10$ ，将其存入答案的千位，再将 $109$ 模 $10$ ，得 $9$ ，将其存入答案的百位；

最后，千位的 $10$ 大于等于 $10$ ，所以将 $10$ （整）除以 $10$ ，得 $1$ ，将其存入答案的万位，再将 $10$ 模 $10$ ，得 $0$ ，将其存入答案的千位；得到答案 $10947$ 。

高精度乘高精度

我们通过高精度乘低精度可以看出，运算 $89\times 123$ ，实际就是将 $123$ 分解成 $1\times 10^{2}+2\times 10^{1}+3\times 10^{0}$ ，再分别用每一位去乘 $89$ 。

高精度乘高精度也是一样的。若还想计算高精度乘高精度的 $89 \times 123$ ，我们就可以受高精度乘低精度的启发，将 $89$ 和 $123$ 分解成 $8 \times 10^{1}+9\times 10^{0}$ 和 $1\times 10^{2}+2\times 10^{1}+3\times 10^{0}$ ，再分别相乘，即 $9\times 10^{0}\times 3\times 10^{0}+8 \times 10^{1}\times 3\times 10^{0}+9\times 10^{0}\times 2\times 10^{1}+8 \times 10^{1}\times 2\times 10^{1}+9\times 10^{0}\times 1\times 10^{2}+8 \times 10^{1}\times 1\times 10^{2}$ ，化简，得 $9\times 3\times 10^{0}+8 \times 3\times 10^{1}+9\times 2\times 10^{1}+8 \times 2\times 10^{2}+9\times 1\times 10^{2}+8 \times 1\times 10^{3}$ 。

从这个复杂的式子上可以看出，若当前两个乘数分别的位置 $i$ 和 $j$ 相乘时，答案会存储在 $i+j$ 这个位置上。

嗯，有点复杂，结合代码食用会好一些。

代码

下面给出高精度乘法的代码：

void mul(int a[],int b[],int c[]){
	clear(c);
	for(int i=0;i<L-1;i++){
		for(int j=0;j<=i;j++)
			c[i]+=a[j]*b[i-j];
		if(c[i]>=10){
			c[i+1]+=c[i]/10;
			c[i]%=10;
		}
	}
}

上一篇-高精度减法的实现 C++算法基础专栏文章下一篇-高精度除法的实现

每周六更新一篇文章，内容一般是自己总结的经验或是在其他网站上整理的优质内容

点个赞，关注一下呗~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1848830.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！