数据结构 —— 线索二叉树
- 线索二叉树
- 结构定义
- 结点类
- 树类
- 线索化
- 找线索二叉树的后继
- 找线索二叉树的前驱
我们今天来看看线索二叉树。
线索二叉树
线索二叉树（Threaded Binary Tree）是一种特殊的二叉树结构，它是在二叉树的基础上进行改良的数据结构，主要是为了解决二叉树在空指针上的遍历效率问题。其提出的背景主要基于以下几个方面：
- 空指针浪费空间：在传统的二叉树中，每个节点都有两个指针分别指向其左孩子和右孩子。对于叶子节点或者缺失孩子的节点，这些指针会指向
NULL，这在大规模数据结构中会浪费大量的存储空间，尤其是当树的深度较大时。
- 遍历效率问题：在遍历二叉树时（如前序、中序、后序遍历），需要不断地检查节点的左右孩子是否为空，这增加了算法的时间复杂度。特别是在中序遍历中，需要重复地回到上一层节点，以访问右子树，这种回溯操作降低了遍历的效率。
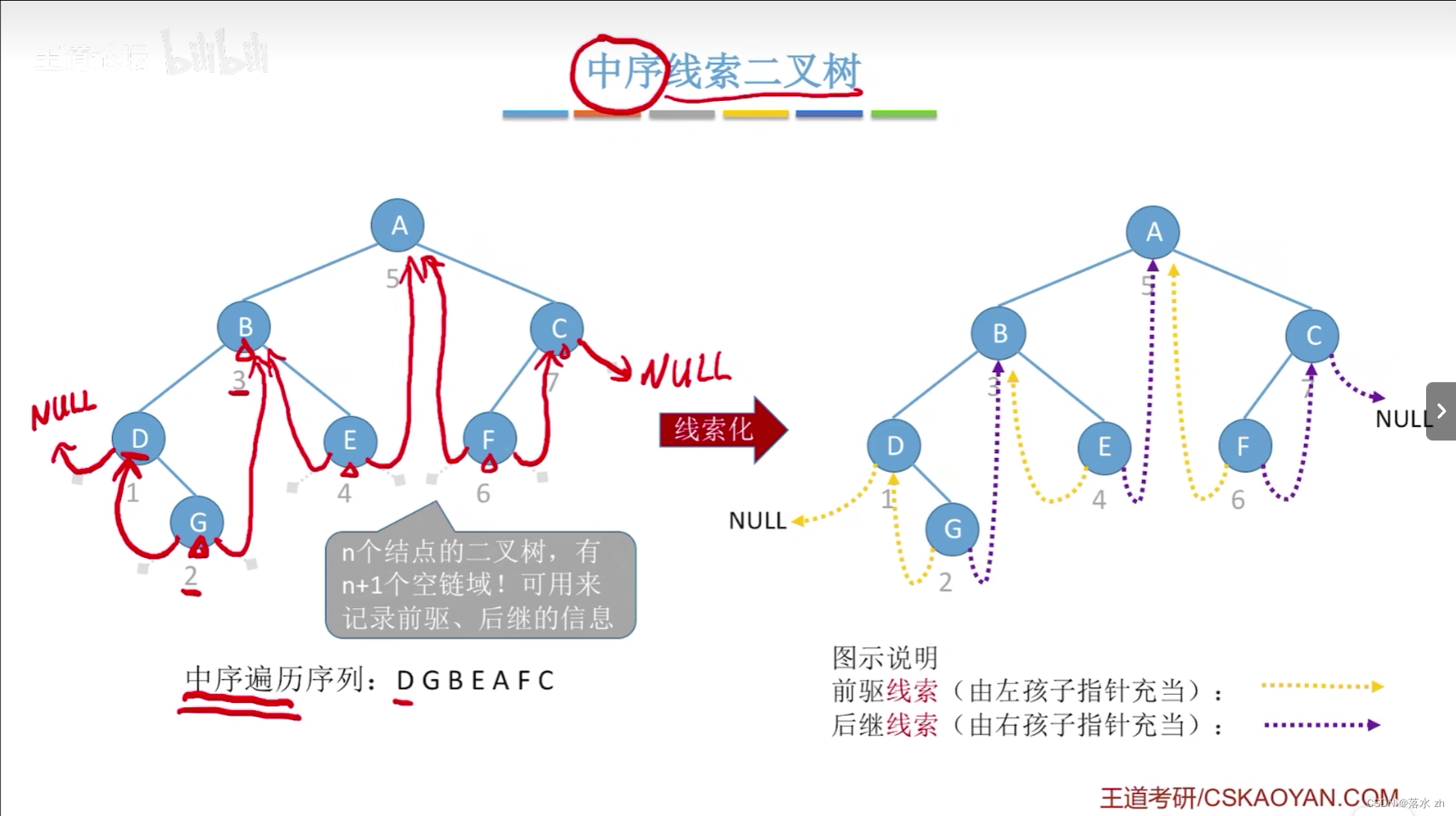
为了解决这些问题，线索二叉树的概念被提出。在线索二叉树中，将那些空的指针（指向NULL的指针）改用来指向某种顺序下的下一个节点（前驱或后继节点），这样就形成了一种链式的结构，使得遍历更加高效。具体来说：
- 线索化：将空的左指针指向该节点在某种遍历顺序下的前驱节点，将空的右指针指向后继节点。
- 标志位：为了区分指针是指向孩子节点还是线索（前驱/后继节点），每个节点通常会增加两个标志位，指示左指针和右指针是否为线索。
通过这种方式，线索二叉树可以在不增加额外存储空间的前提下，实现对二叉树的快速遍历，尤其是在频繁进行中序遍历等操作时，能够显著提高效率。
结构定义
结点类
我们还是首先把结点类创造出来：
// 定义二叉树结点
template<class T>
class BTreeNode
{
public:
// 构造函数，初始化结点数据、左孩子和右孩子指针
BTreeNode(T data)
: _data(data)
, _leftchild(nullptr)
, _rightchild(nullptr)
{
}
// 数据
T _data;
// 左右孩子指针
BTreeNode<T>* _leftchild;
BTreeNode<T>* _rightchild;
// 线索化标志，用于标记当前结点的左指针是否为线索
int lflag = 0;
// 线索化标志，用于标记当前结点的右指针是否为线索
int rflag = 0;
};
树类
然后我们根据这个结点，创建一个线索二叉树类，这里创建一棵二叉搜索树：
// 定义线索二叉树
template<class T>
class ThreadBTree
{
public:
// 构造函数，初始化根结点
ThreadBTree(T data)
{
_root = new BTreeNode<T>(data);
}
// 插入结点到二叉树中
void _Insert(BTreeNode<T>*& root, T data)
{
if (root == nullptr)
{
root = new BTreeNode<T>(data);
return;
}
// 根据数据大小，将结点插入到左子树或右子树
if (root->_data< data)
{
_Insert(root->_rightchild, data);
}
else if (root->_data > data)
{
_Insert(root->_leftchild, data);
}
}
// 外部调用接口，插入结点到二叉树中
void Insert(T data)
{
_Insert(_root, data);
}
// 中序遍历二叉树
void _Inorder(BTreeNode<T>* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_leftchild);
//操作
std::cout << root ->_data << " ";
_Inorder(root->_rightchild);
}
// 外部调用接口，中序遍历二叉树
void Inorder()
{
_Inorder(_root);
}
private:
BTreeNode<T>* _root; // 根结点指针
};
这样我们建立好了一棵二叉搜索树，我们插入几个数试试：
#include "ThreadBTree.h"
int main()
{
ThreadBTree<int> bt(23);
bt.Insert(44);
bt.Insert(1);
bt.Insert(2);
bt.Insert(29);
bt.Insert(7);
bt.Inorder();
std::cout << std::endl;
return 0;
}
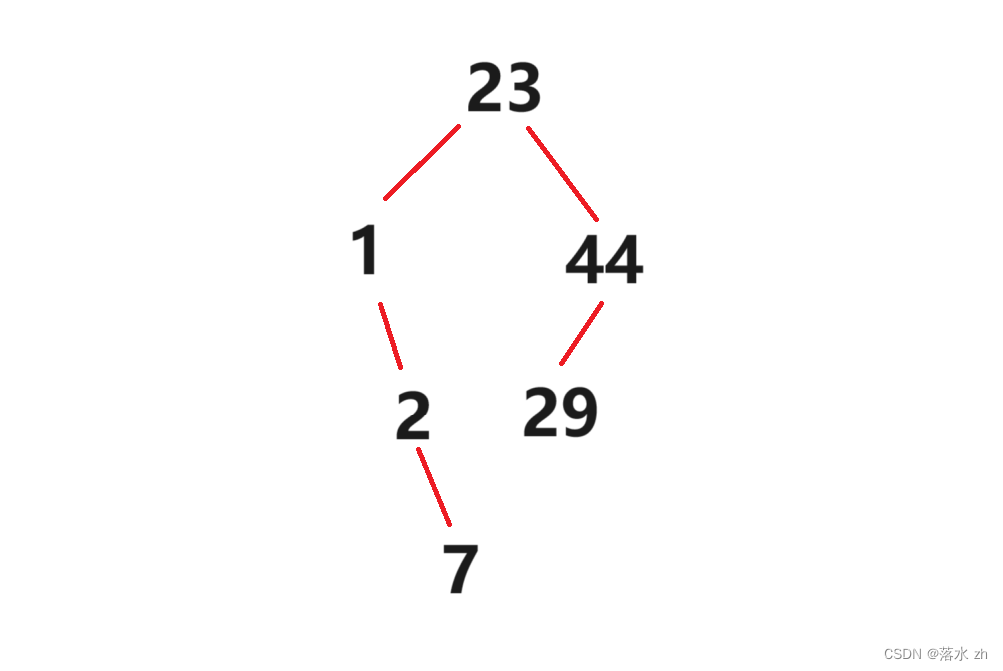
构建了像这样的一棵搜索二叉树：
线索化
现在我们可以对这棵二叉树进行线索化，我们先来看看这棵树有多少的空指针域：
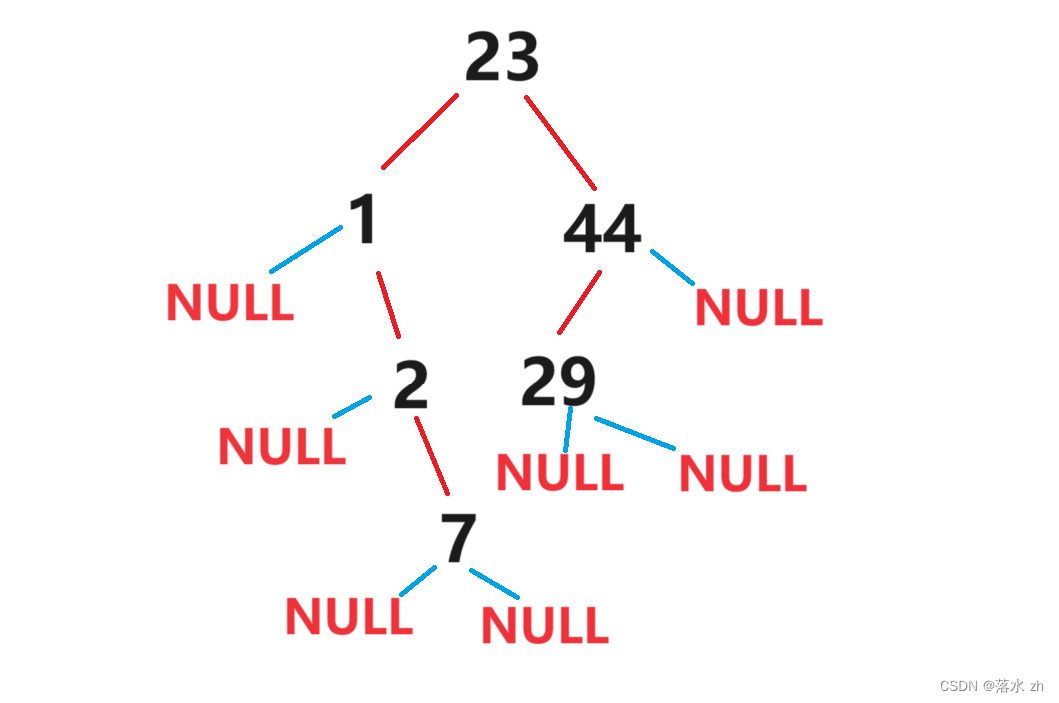我们这里采用模拟中序，然后线索化，我们定义一个prve指针，记录当前上一步到哪里。
但是这里注意，一开始prve为空，可以当做第一个结点的NULL：
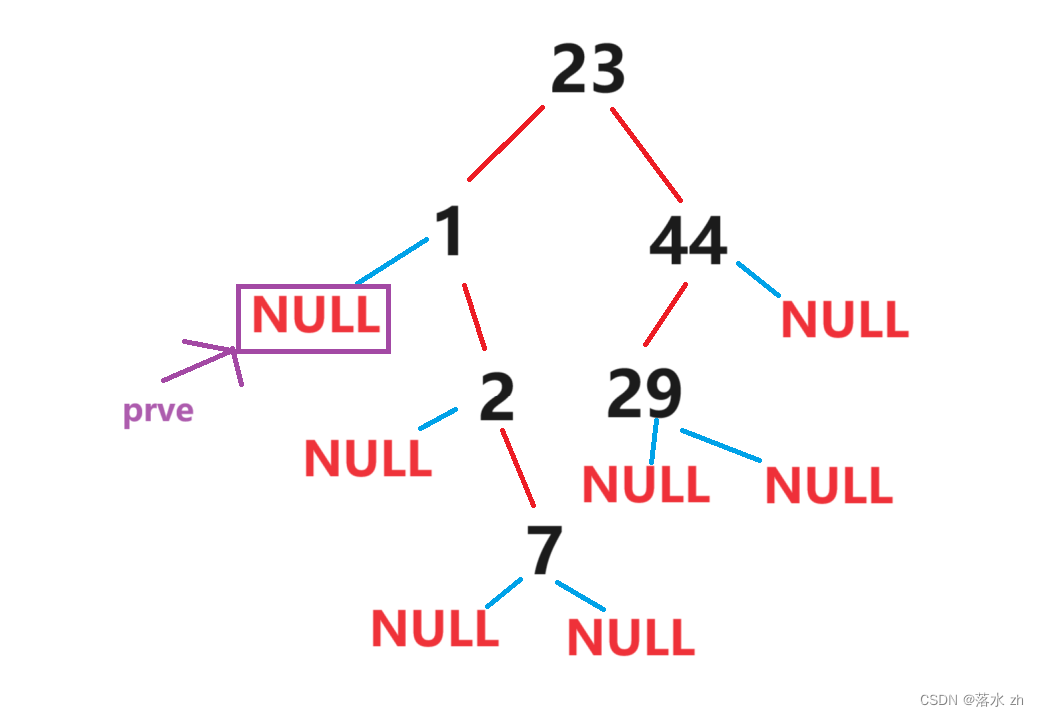然后定义一个cur指针，从根节点开始：
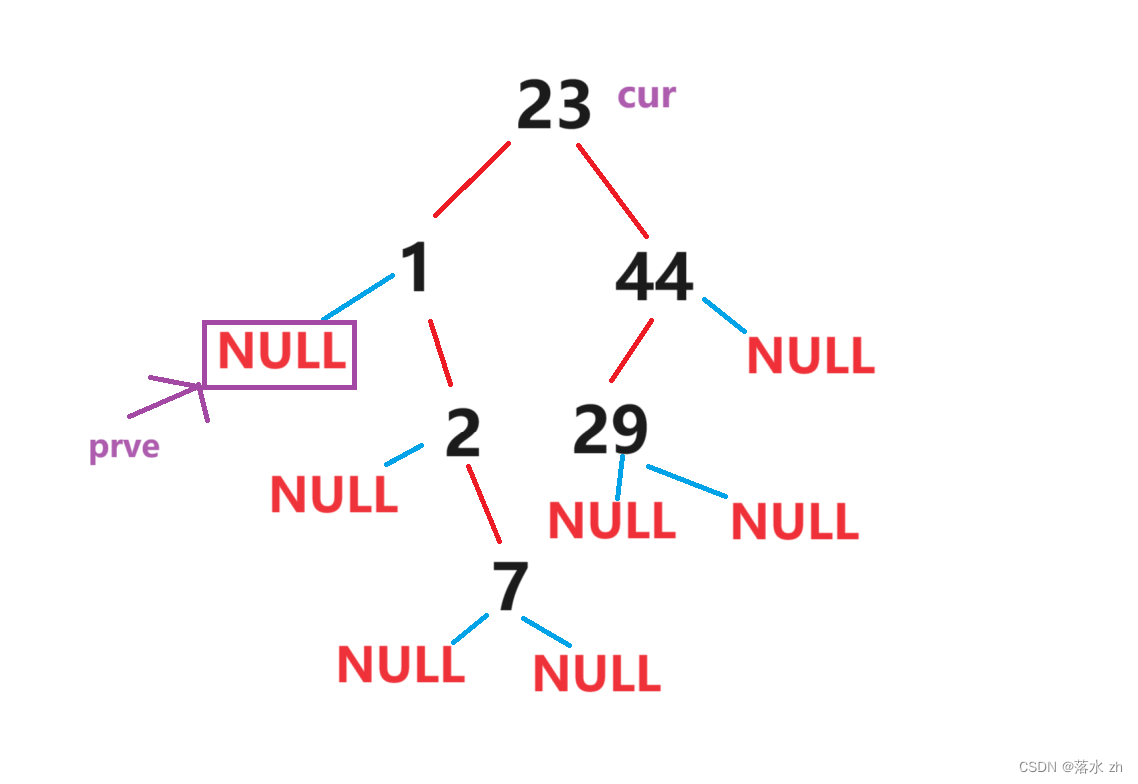
然后cur到了1这里：
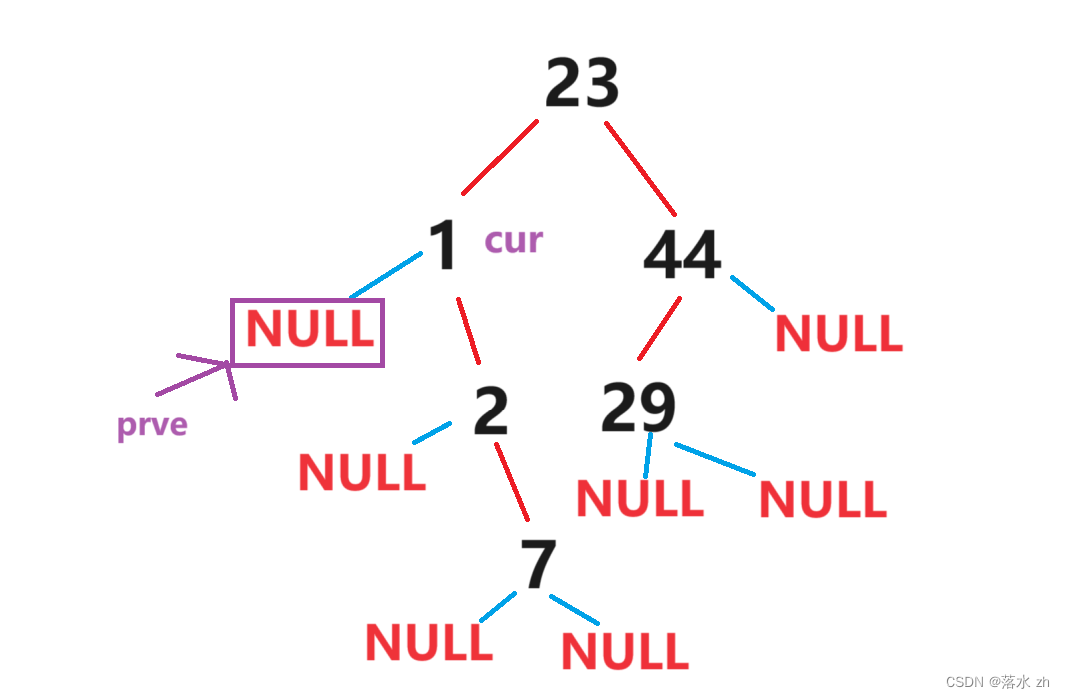
然后prve开始记录cur路径，当cur到2的时候，prve到1：
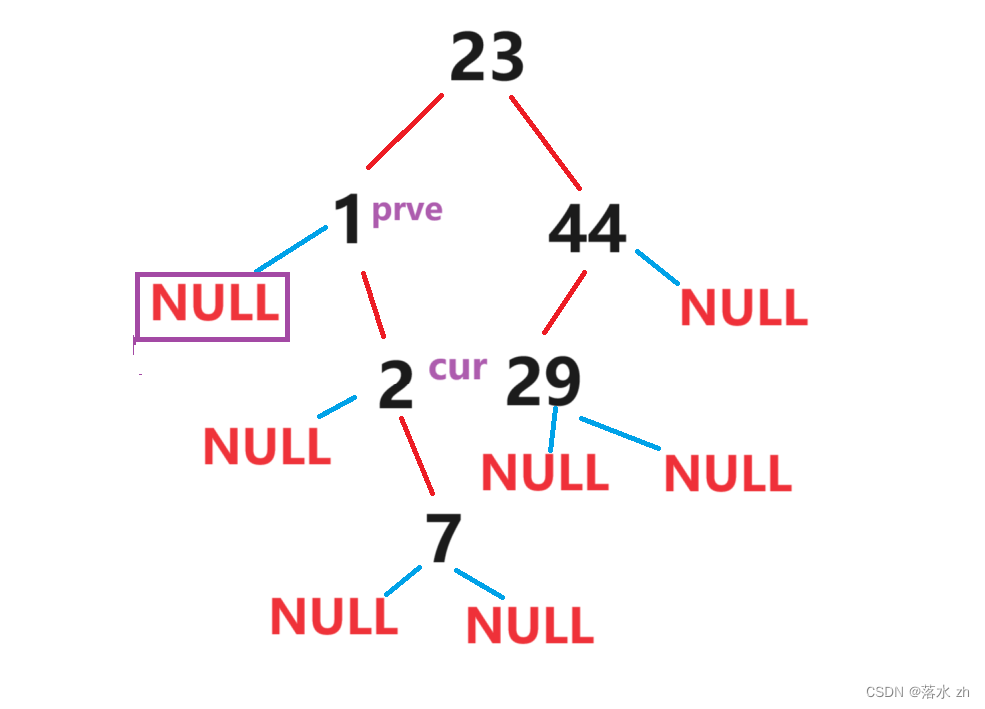这个时候cur左孩子为空，修改cur左孩子标志位，标志此时左孩子担任线索，并指向prve：
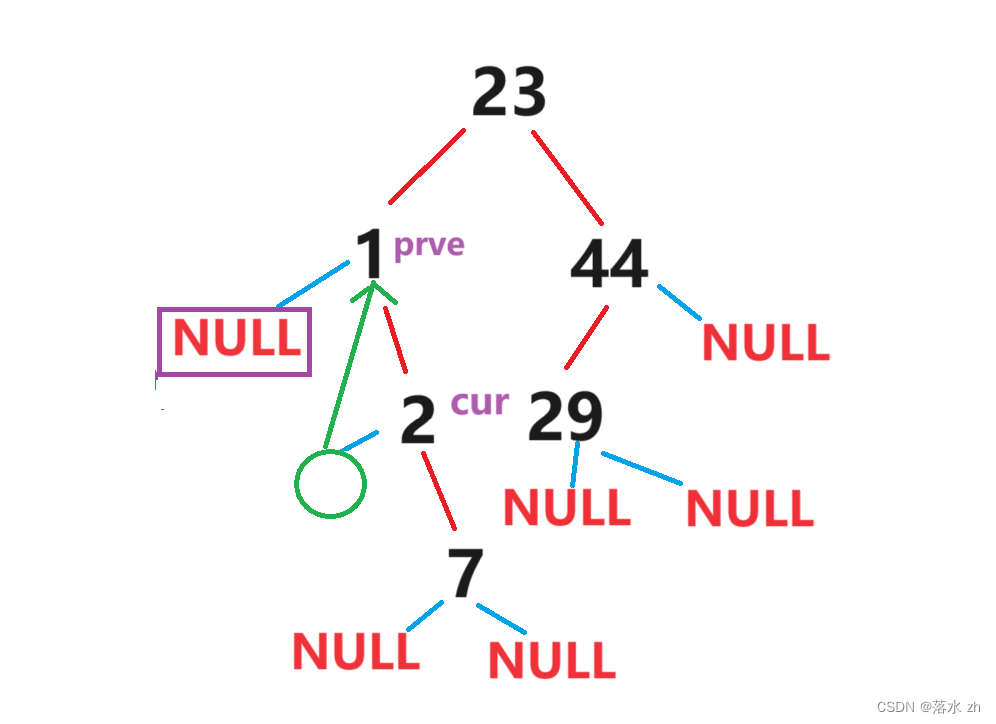依次类推，2和7也是这样，到7这里，左孩子也可以作为线索：
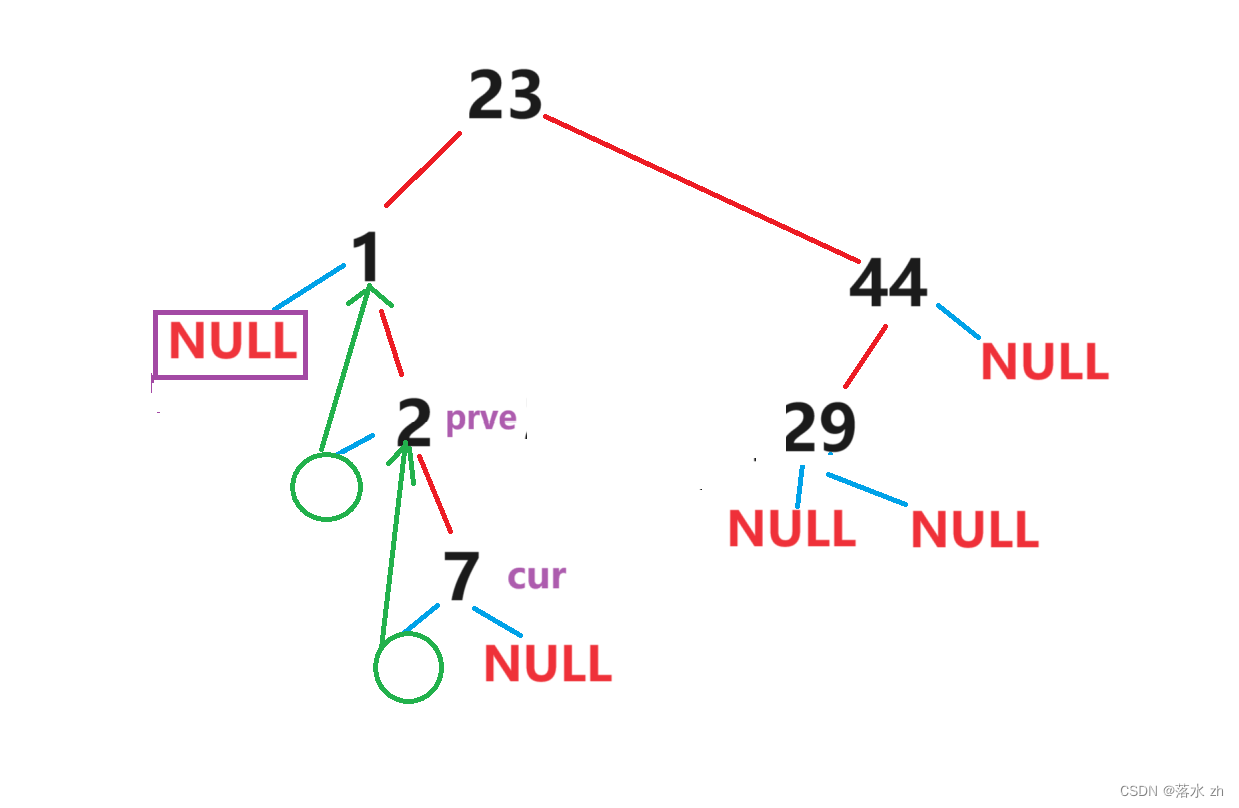
这样我们可以写出前半段代码：
// 线索化处理函数
void vist(BTreeNode<T>* cur)
{
// 如果当前结点的左孩子为空，将当前结点的左指针指向前一个结点，并设置线索化标志
if (cur->_leftchild == nullptr)
{
cur->_leftchild = _prve;
cur->lflag = 1;
}
// 更新前一个结点为当前结点
_prve = cur;
}
接下来，cur会走到23，prve会走到7：
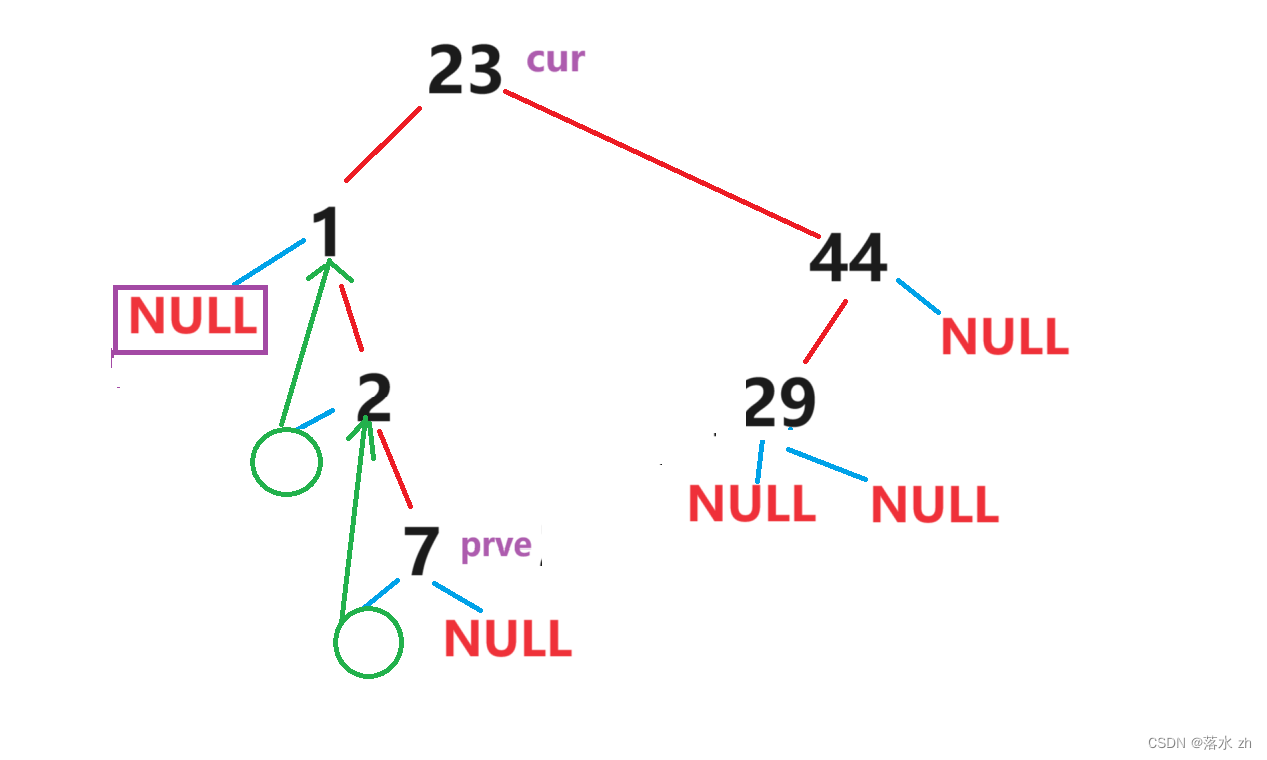这个时候cur是prve的后继：
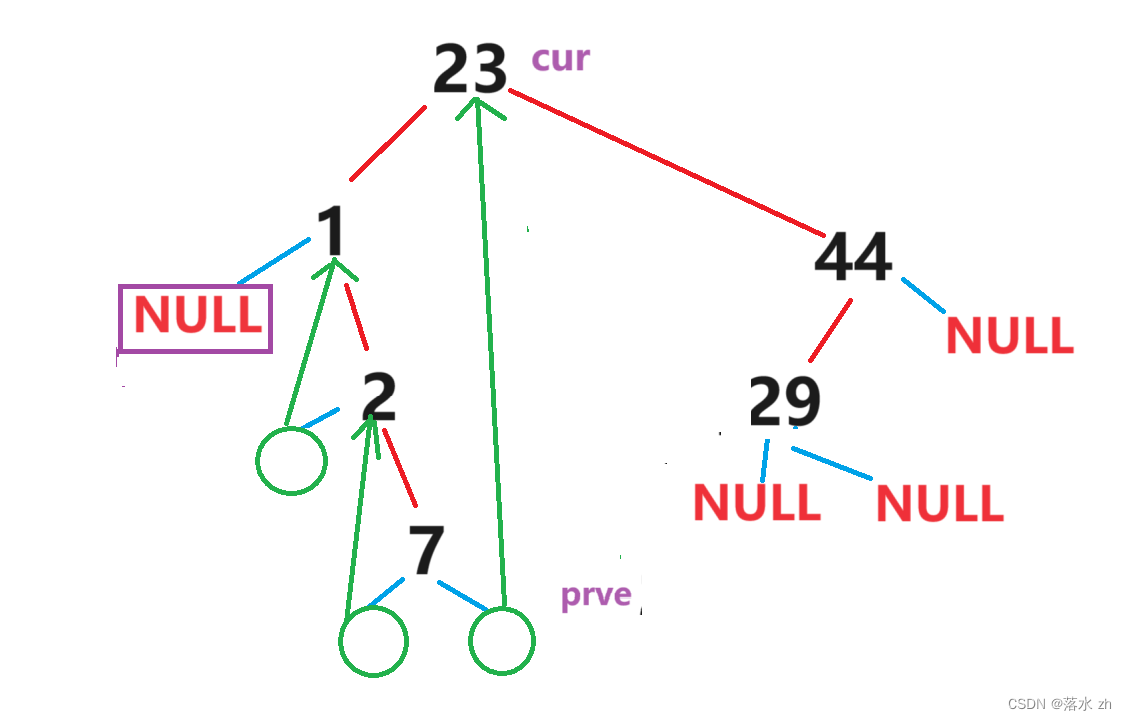
我们写出后半段的代码：
// 线索化处理函数
void vist(BTreeNode<T>* cur)
{
// 如果当前结点的左孩子为空，将当前结点的左指针指向前一个结点，并设置线索化标志
if (cur->_leftchild == nullptr)
{
cur->_leftchild = _prve;
cur->lflag = 1;
}
// 如果前一个结点的右孩子为空，将前一个结点的右指针指向当前结点，并设置线索化标志
if (_prve != nullptr && _prve->_rightchild == nullptr)
{
_prve->_rightchild = cur;
_prve->rflag = 1;
}
// 更新前一个结点为当前结点
_prve = cur;
}
我们改造一下线索二叉树类：
#pragma once
#include<iostream>
// 定义二叉树结点
template<class T>
class BTreeNode
{
public:
// 构造函数，初始化结点数据、左孩子和右孩子指针
BTreeNode(T data)
: _data(data)
, _leftchild(nullptr)
, _rightchild(nullptr)
{
}
// 数据
T _data;
// 左右孩子指针
BTreeNode<T>* _leftchild;
BTreeNode<T>* _rightchild;
// 线索化标志，用于标记当前结点的左指针是否为线索
int lflag = 0;
// 线索化标志，用于标记当前结点的右指针是否为线索
int rflag = 0;
};
// 定义线索二叉树
template<class T>
class ThreadBTree
{
public:
// 构造函数，初始化根结点
ThreadBTree(T data)
{
_root = new BTreeNode<T>(data);
}
// 插入结点到二叉树中
void _Insert(BTreeNode<T>*& root, T data)
{
if (root == nullptr)
{
root = new BTreeNode<T>(data);
return;
}
// 根据数据大小，将结点插入到左子树或右子树
if (root->_data< data)
{
_Insert(root->_rightchild, data);
}
else if (root->_data > data)
{
_Insert(root->_leftchild, data);
}
}
// 外部调用接口，插入结点到二叉树中
void Insert(T data)
{
_Insert(_root, data);
}
// 中序遍历二叉树
void _Inorder(BTreeNode<T>* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_leftchild);
//vist(root); // 访问当前结点，进行线索化处理
std::cout << root ->_data << " ";
_Inorder(root->_rightchild);
}
// 外部调用接口，中序遍历二叉树
void Inorder()
{
_Inorder(_root);
}
// 线索化处理函数
void vist(BTreeNode<T>* cur)
{
// 如果当前结点的左孩子为空，将当前结点的左指针指向前一个结点，并设置线索化标志
if (cur->_leftchild == nullptr)
{
cur->_leftchild = _prve;
cur->lflag = 1;
}
// 如果前一个结点的右孩子为空，将前一个结点的右指针指向当前结点，并设置线索化标志
if (_prve != nullptr && _prve->_rightchild == nullptr)
{
_prve->_rightchild = cur;
_prve->rflag = 1;
}
// 更新前一个结点为当前结点
_prve = cur;
}
private:
BTreeNode<T>* _root; // 根结点指针
BTreeNode<T>* _prve = nullptr; // 用于记录中序遍历过程中的前一个结点
BTreeNode<T>* _cur = _root; // 当前遍历到的结点，默认为根结点
};
找线索二叉树的后继
现在我们有了一棵线索化的二叉树，现在我们想给定一个结点，找它的后继结点：
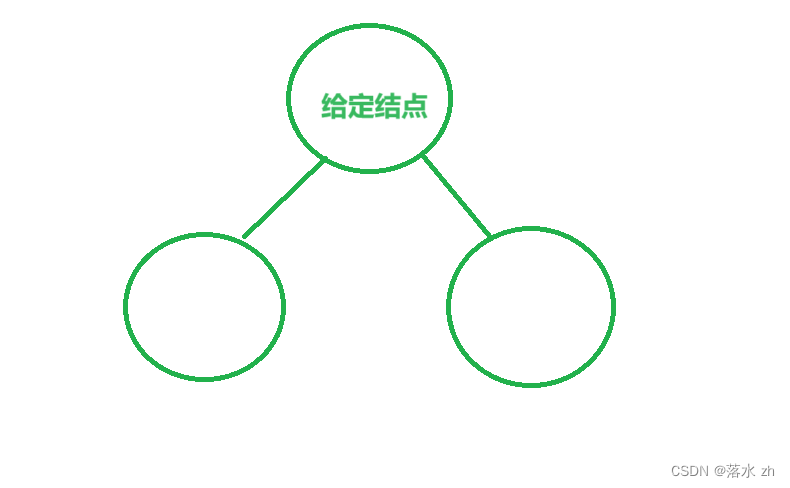
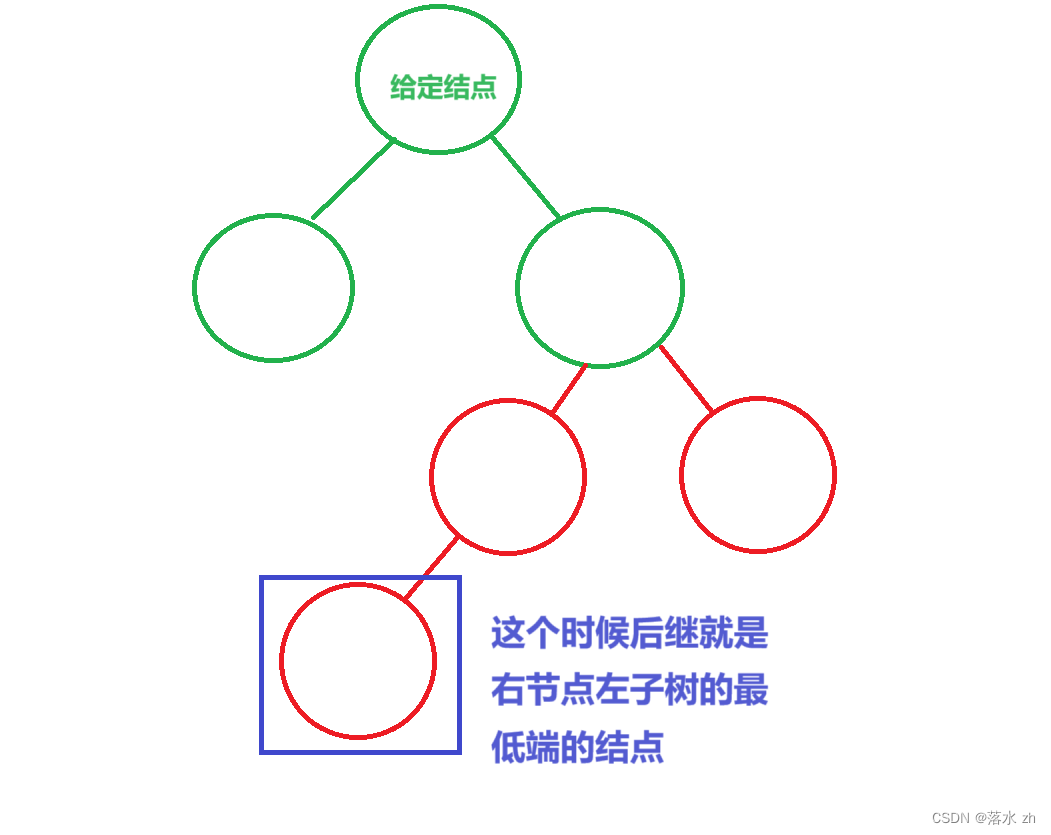
如果给定结点的右子树只有一个结点，则后继结点就是这个结点，但是如果右节点的左子树有结点：
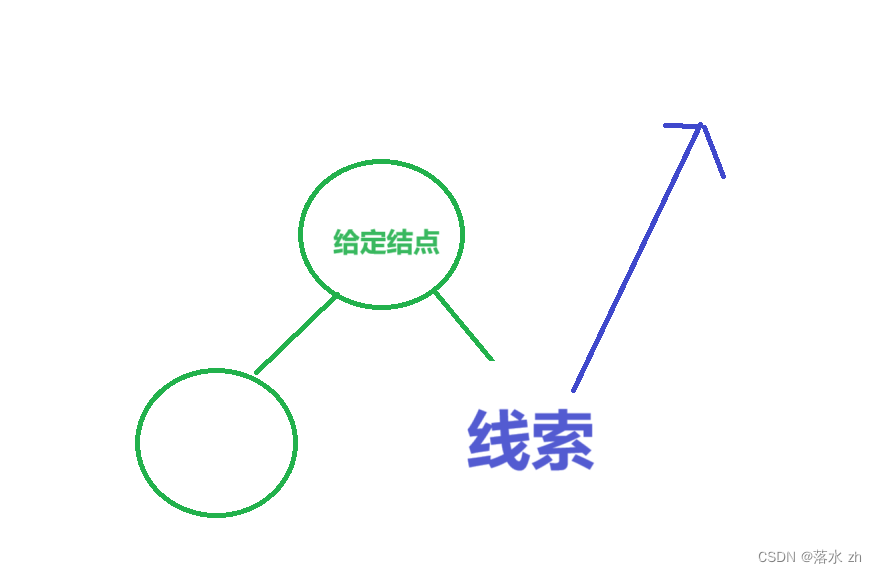
如果没有结点，则右孩子为线索，直接返回线索：
BTreeNode<T>* FisrtNode(BTreeNode<T>* node)
{
// 循环向下遍历，直到找到一个左标志为1的节点（表示左孩子是线 索，指向实际节点）
while (node->lflag == 0)
{
node = node->_leftchild;
}
return node; // 返回第一个实际节点
}
BTreeNode<T>* NextNode(BTreeNode<T>* node)
{
if (node->rflag == 0)
return FisrtNode(node->_rightchild);
else if (node->rflag == 1)
return node->_rightchild;
}
BTreeNode<T>* FindNode(T data)
{
return _FindNode(_root, data);
}
BTreeNode<T>* _FindNode(BTreeNode<T>* root, T data)
{
if (root->_data == data)
{
return root;
}
if (root->_data < data)
{
return _FindNode(root->_rightchild, data);
}
else if (root->_data > data)
{
return _FindNode(root->_leftchild, data);
}
return nullptr;
}
找线索二叉树的前驱
找前驱和找后继的逻辑差不多：
BTreeNode<T>* FisrtNode2(BTreeNode<T>* node)
{
while (node->rflag == 0)
{
node = node->_rightchild;
}
return node;
}
BTreeNode<T>* NextNode2(BTreeNode<T>* node)
{
if (node->lflag == 0)
return FisrtNode(node->_leftchild);
else if (node->lflag == 1)
return node->_leftchild;
}
我们来试试：
#include "ThreadBTree.h"
int main()
{
ThreadBTree<int> bt(23);
bt.Insert(44);
bt.Insert(1);
bt.Insert(2);
bt.Insert(29);
bt.Insert(7);
bt.Inorder();
BTreeNode<int>* node = bt.FindNode(7);
BTreeNode<int>* next_node = bt.NextNode(node);
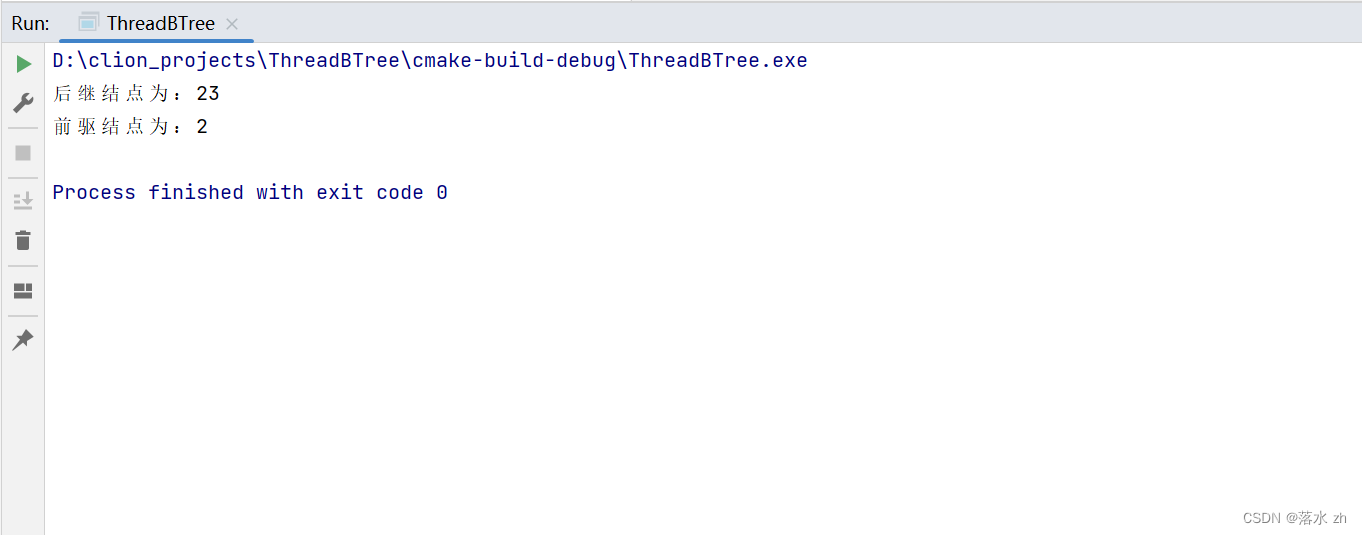
std::cout << "后继结点为：" << next_node->_data << std::endl;
BTreeNode<int>* prve_node = bt.NextNode2(node);
std::cout << "前驱结点为：" << prve_node->_data << std::endl;
return 0;
}
![[FlareOn5]Ultimate Minesweeper](https://img-blog.csdnimg.cn/direct/e6c0184fd9f543a497fbeebe8994c8ef.png)
