文章目录
- 离散数学与组合数学-08谓词逻辑
- 8.1 谓词的引入
- 8.1.1 引入谓词逻辑
- 8.1.2 个体词与谓词
- 8.2 量词的引入
- 8.2.1 量词引入
- 8.2.2 个体域符号化
- 8.2.3 量词真值确定
- 8.3 谓词符号化举例
- 8.3.1 示例一
- 8.3.2 示例二
- 8.3.3 示例三
- 8.3.4 示例四
- 8.4 谓词合式公式
- 8.4.1 四类符号
- 8.4.2 项
- 8.4.3 合式公式
- 8.5 自由变元与约束变元
- 8.5.1 定义
- 8.5.2 判定
- 8.5.3 两个规则
- 8.5.4 闭式
- 8.6 公式的解释与分类
- 8.6.1 公式的解释
- 8.6.2 公式的分类
- 8.7 公式的等价关系
- 8.7.1 定义
- 8.7.2 基本等价关系
- 8.8 前束范式
- 8.8.1 定义
- 8.8.2 求解步骤
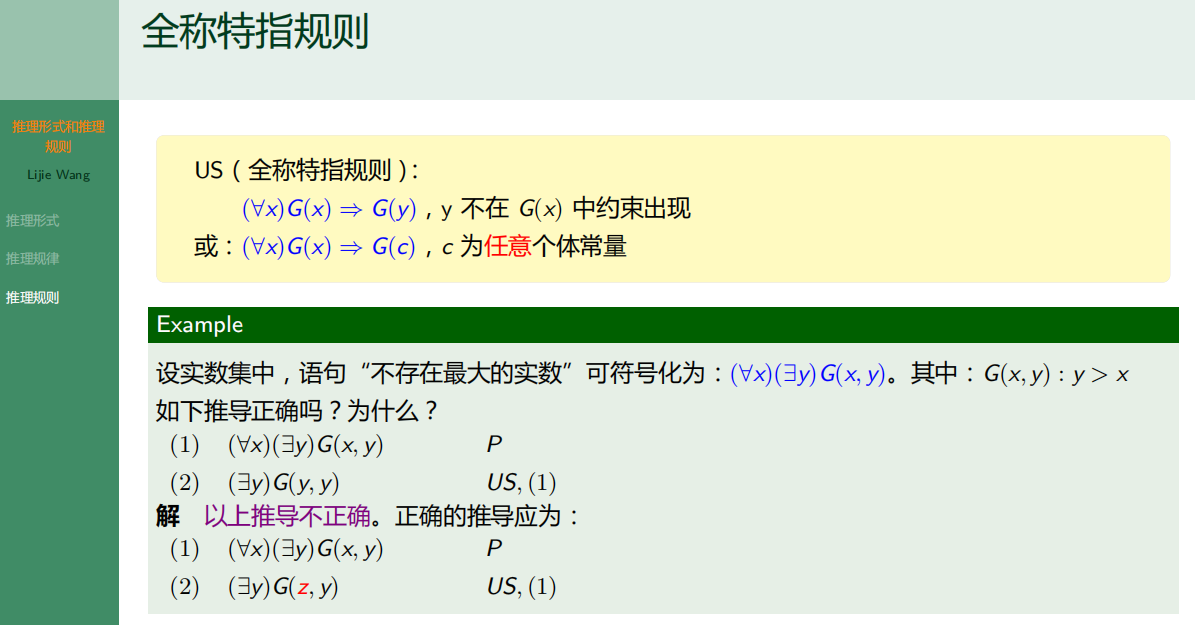
- 8.9 推理形式与推理规则
- 8.9.1 推理形式
- 8.9.2 推理规律
- 8.9.3 推理规则
本文为离散数据与组合数学电子科技大学王丽杰老师的课程笔记,详细视频参考
【电子科技大学】离散数学(上) 王丽杰
【电子科技大学】离散数学(下) 王丽杰
latex的离散数学写法参考: 离散数学与组合数学-01
离散数学公式
!符号 代码 含义
∧
\wedge
∧ \wedge 且
∨
\vee
∨ \vee 或
∩
\cap
∩ \cap 交
∪
\cup
∪ \cup 并
⊆
\subseteq
⊆ \subseteq 子集
⊈
\nsubseteq
⊈ \nsubseteq 不是子集
⊂
\subset
⊂ \subset 真子集
⊄
\not\subset
⊂ \not\subset 不是真子集
∈
\in
∈ \in 属于
∉
\not\in
∈ \not\in 不属于
↔
\leftrightarrow
↔ \leftrightarrow 等价
⇔
\Leftrightarrow
⇔ \Leftrightarrow 等值
¬
\neg
¬ \neg或\lnot 非
R
\mathbb{R}
R \mathbb{R} 实数集
Z
\mathbb{Z}
Z \mathbb{Z} 整数集
∅
\varnothing
∅ \varnothing 空集
∀
\forall
∀ \forall 对任意的
∃
\exists
∃ \exists 存在
≥
\geq
≥ \geq大于等于
≤
\leq
≤ \leq 小于等于
下标的输入命令是:
x
内容
x_{内容}
x内容 x_{内容}
上标的输入命令式:
x
2
x^2
x2 x^2
空格 \quad
R / R\mkern-10.5mu/ R/ R\mkern-10.5mu/ 数值越大,斜杆越往字母左侧移动
离散数学与组合数学-08谓词逻辑
8.1 谓词的引入
8.1.1 引入谓词逻辑

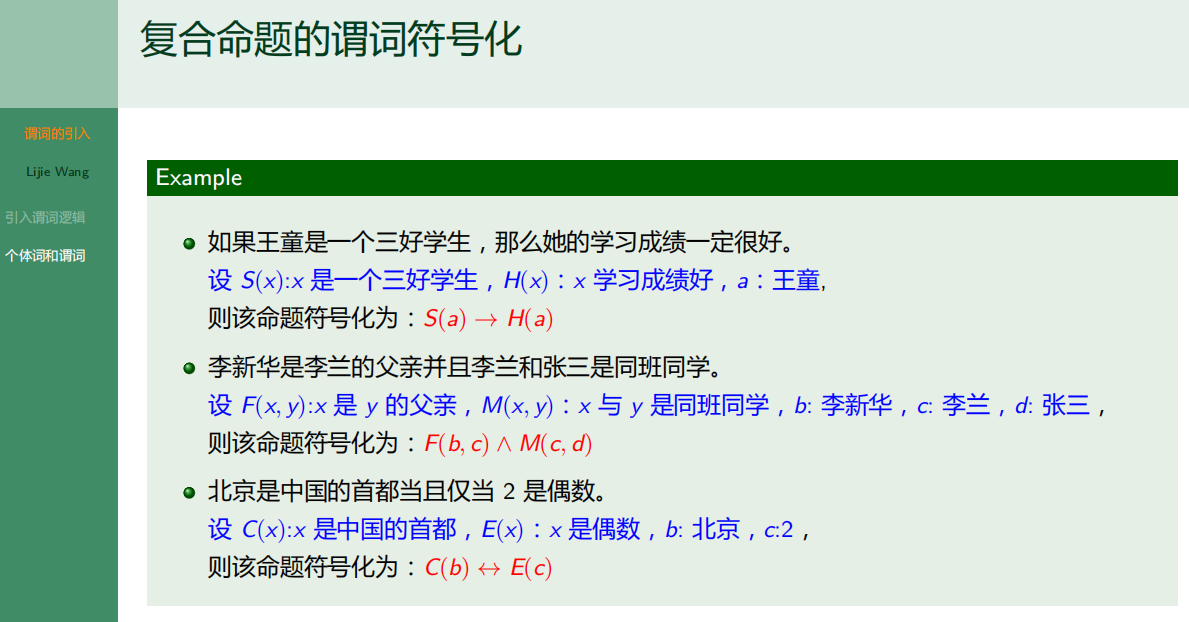
8.1.2 个体词与谓词





8.2 量词的引入
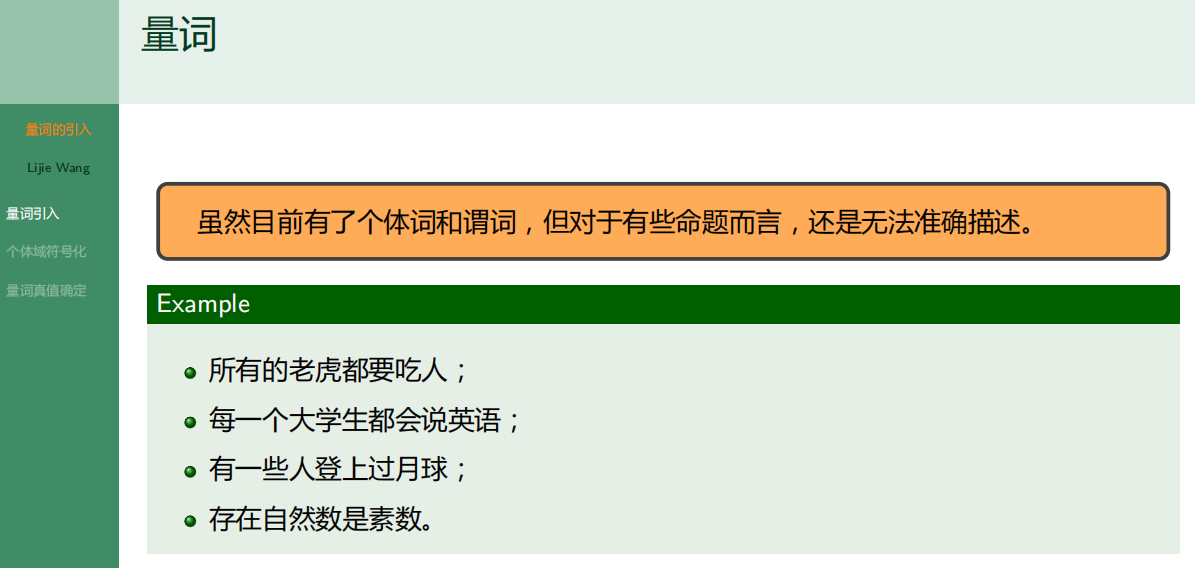
8.2.1 量词引入

8.2.2 个体域符号化


8.2.3 量词真值确定



8.3 谓词符号化举例
8.3.1 示例一

8.3.2 示例二

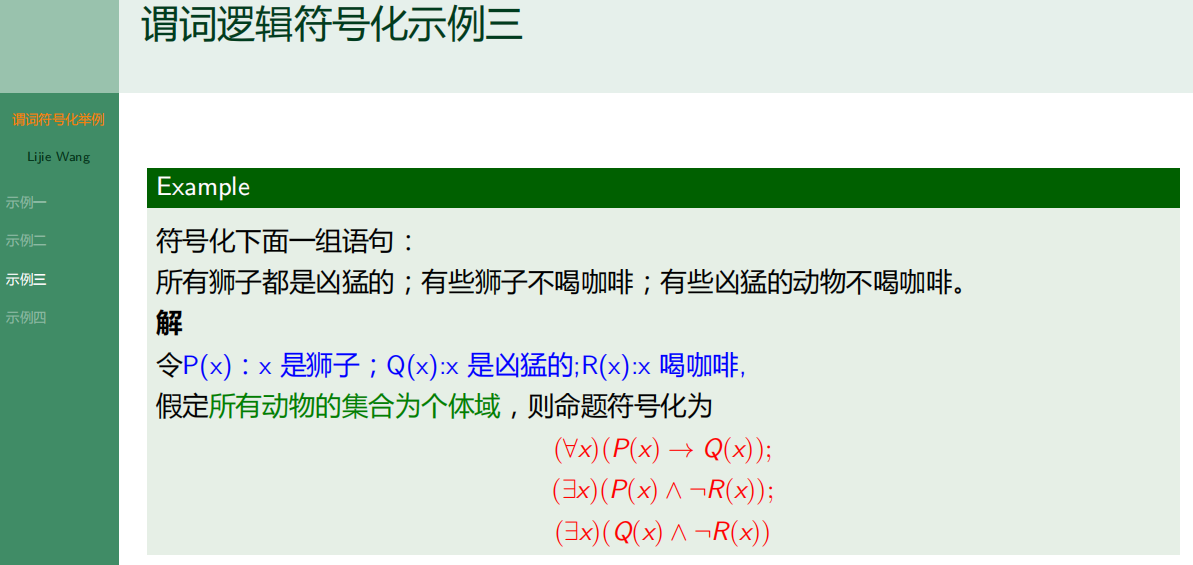
8.3.3 示例三
8.3.4 示例四

8.4 谓词合式公式
8.4.1 四类符号


8.4.2 项

8.4.3 合式公式


8.5 自由变元与约束变元
8.5.1 定义
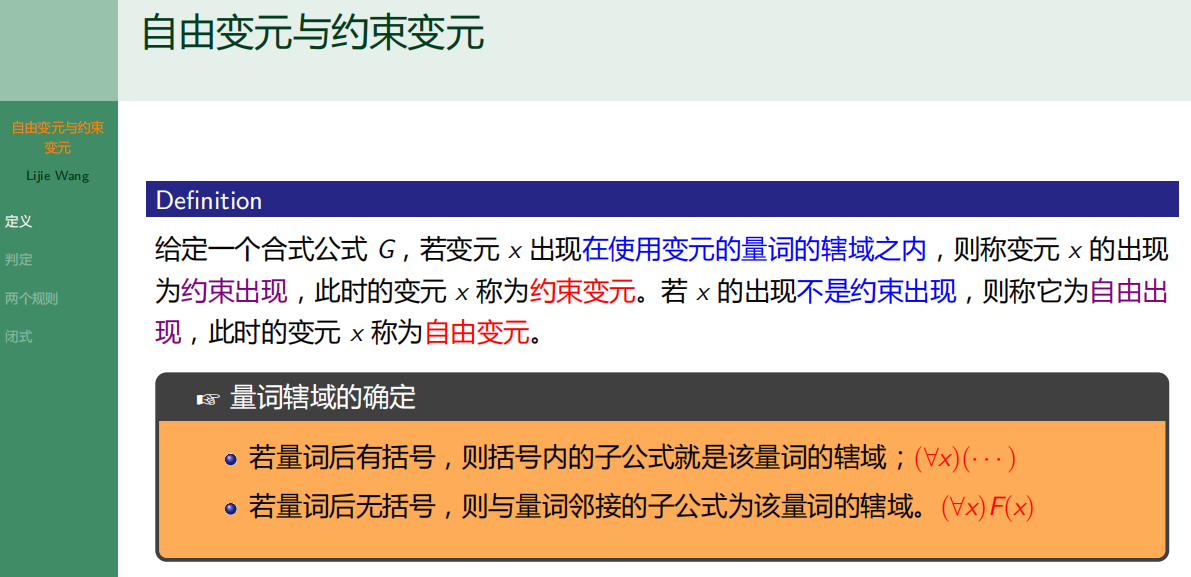
8.5.2 判定

8.5.3 两个规则

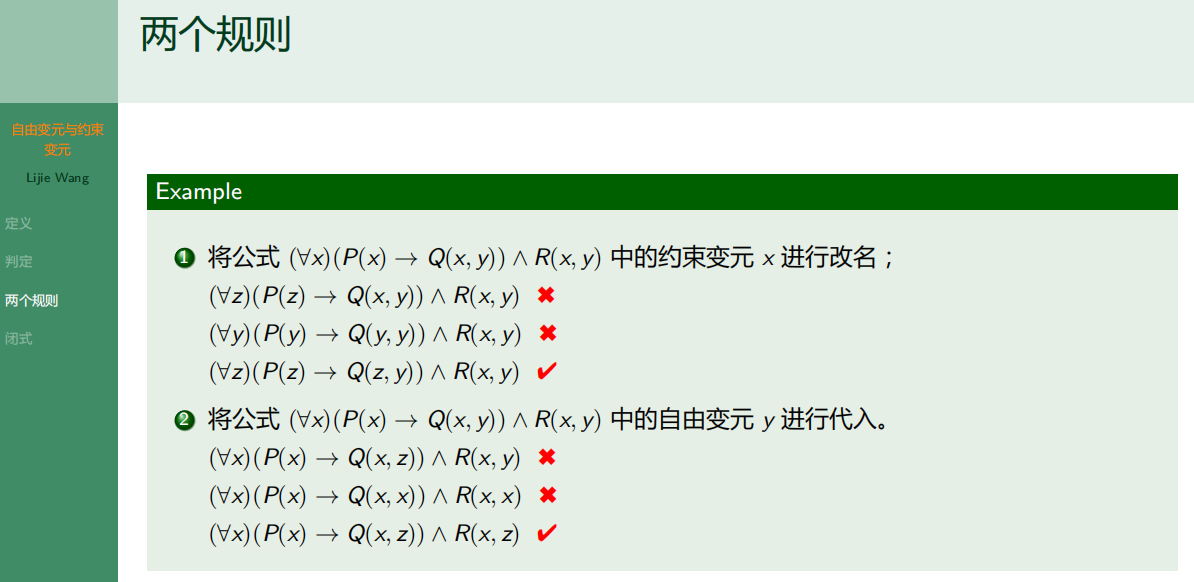
8.5.4 闭式
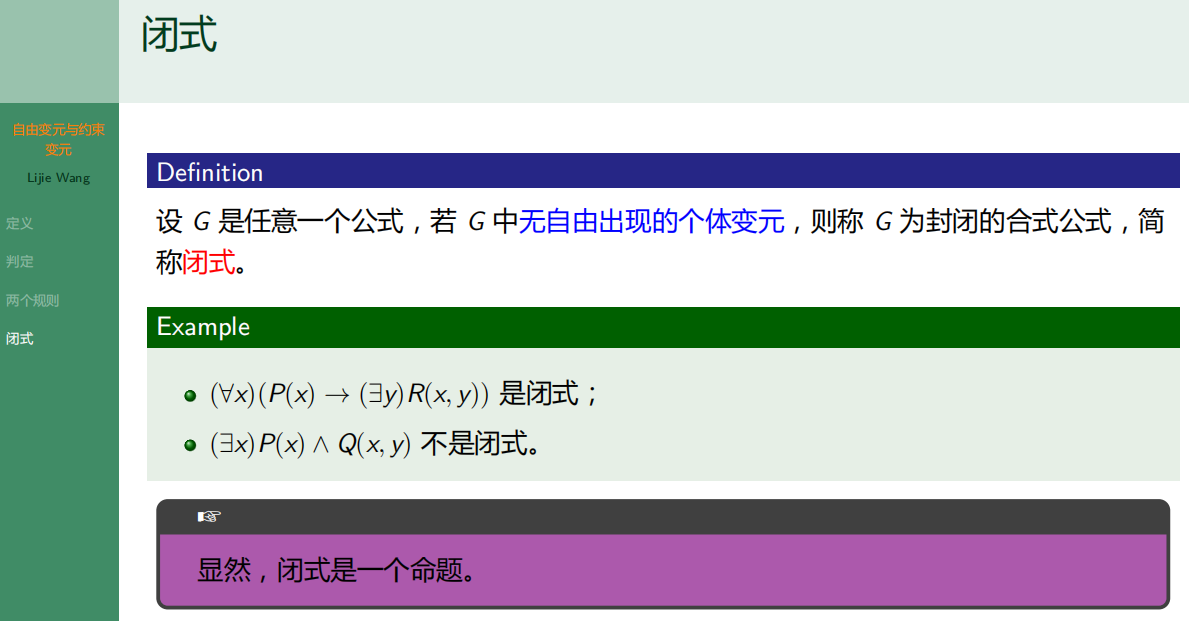
8.6 公式的解释与分类
8.6.1 公式的解释


8.6.2 公式的分类


8.7 公式的等价关系
8.7.1 定义

8.7.2 基本等价关系



8.8 前束范式
8.8.1 定义

8.8.2 求解步骤


8.9 推理形式与推理规则
8.9.1 推理形式

8.9.2 推理规律


8.9.3 推理规则