复分析——第6章—— Γ 函数和 ζ 函数(E.M. Stein R. Shakarchi)

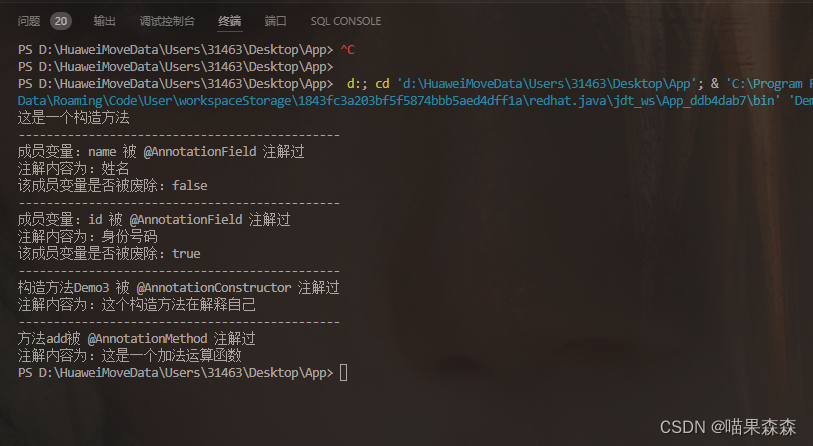
第6章 Γ函数和Ζ函数(The Gamma and Zeta Functions)

毫不夸张地说，Γ函数和Ζ函数是数学中最重要的非初等函数之一。Γ函数在自然界中无处不在。它出现在大量计算中，并以分析中出现的大量恒等式为特征。对此的部分解释可能在于Γ函数的基本结构特性，这些基本结构特性在本质上刻画了它：1/Γ(s)是(最简单)的复可积函数(注：与这个主题的标准记法保持一致，我们用s(而不是z)表示Γ函数和ζ 函数的参数)，其恰好在 s = 0, -1, -2 ，…… 处有零点。

ζ 函数(和Γ函数一样，对其研究是由Euler发起的)在数论分析中起着重要作用。它与素数的密切联系通过ζ(s)的恒等式体现出来：

$\displaystyle \prod_{p}\frac{1}{1-p^{-s}} = \sum_{n=1}^{\infty}\frac{1}{n^s}$ ，

其中，乘积覆盖所有素数。实数 s > 1 且趋近于1 的ζ(s)的行为被 Euler 用于证明 $\sum_{p}1/p$ 发散，并且，正如我们在第I册书中看到的那样，L 函数的类似推理是算术级数中素数Dirichlet定理证明的起点。

然而，不难看出，当 Re(s) > 1 时，ζ(s)是定义明确的(且可分析的)，是Riemann意识到，对素数的进一步研究与ζ到复平面其余部分的解析(实际上是亚纯)延拓(continuation)密切相关。除此之外，我们还考虑其显著的函数方程，它揭示了关于直线 Re(s) = 1/2 的对称性，其证明基于ζ函数的相应恒等式。我们还对直线 Re(s) = 1 附近的 Re(s) 的增长进行了更详细的研究，在下一章将给出的素数定理的证明中便需要它。

1. Γ 函数(The gamma function)

对于 s > 0 ，定义 Γ 函数为

(1) $\displaystyle \Gamma(s) = \int_{0}^{\infty}e^{-t}t^{s-1}dt$ 。

这个积分对于每一个正数 s 收敛，因为在 t = 0 附近函数 $t^{s-1}$ 是可积的，t足够大时的收敛由被积函数中的指数递降特性保证。这些观察结果允许我们按下面的方式扩充Γ函数的定义域。

命题1.1 将Γ函数扩充为半平面R(s) > 0 上的解析函数，其公式仍可由积分公式(1)给出。

证明：

只需证明这个积分定了一个带域(strip)

$S_{\delta,M} = \{ \delta < R(s) < M \} ( 0 < \delta < M < \infty)$

中的全纯函数即可。注意到，若用 σ 表示 s 的实部，则 $|e^{-t} t^{s-1}| = e^{-t} t^{\sigma-1}$ ，因此，积分

$\displaystyle \Gamma(s) = \int_{0}^{\infty}e^{-t}t^{s-1}dt$ ，

其由极限 $\displaystyle \lim_{\epsilon \rightarrow 0} \int_{\epsilon}^{1/\epsilon}e^{-t}t^{s-1}dt$ 所定义，且对于每一个 $s \in S_{\delta,M}$ 收敛。对于ε > 0 ,令

$\displaystyle F_{\epsilon}(s)=\int_{\epsilon}^{1/\epsilon}e^{-t}t^{s-1}dt$ 。

根据第2章定理5.4 ,函数 $F_{\epsilon}$ 在带域 $S_{\delta,M}$ 中是全纯的。根据定理第2章定理5.2 , 只需证明在带域 $S_{\delta,M}$ 上 $F_{\epsilon}$ 一致收敛于Γ 即可。为了理解这一点，我们首先观察到

$\displaystyle \bigg | \Gamma(s) - F_{\epsilon}(s) \bigg | \leq \int_{0}^{\epsilon}e^{-t} t^{\sigma-1} dt + \int_{1/\epsilon}^{\infty}e^{-t}t^{\sigma-1} dt$ 。

上面第一个积分随着 ε 趋近于 0 而一致地趋近于 0 ，因为，只要 0 < ε < 1 ,很容易通过 $\epsilon^{\delta}/{\delta}$ 进行估算。同样，第二个积分也一致地收敛于0，因为

$\displaystyle \bigg | \int_{1/\epsilon}^{\infty}e^{-t}t^{\sigma-1} dt \bigg | \leq \bigg | \int_{1/\epsilon}^{\infty}e^{-t}t^{M-1} dt \bigg | \leq C \bigg | \int_{1/\epsilon}^{\infty}e^{-t/2} dt \bigg | \longrightarrow 0$ 。

因此，证明完结。

1.1 解析延拓(Analytic continuation)

尽管定义 Γ 的积分对于 s的其它值事实上并非绝对收敛，但我们可以进一步证明，存在一个定义于整个ℂ上的全纯函数，其在 Re(s)> 0 的半平面上等于Γ。按照在和第2章中相同的意义上，我们称这个函数为Γ函数的解析延拓(analytic continuation)(注：解析延拓的唯一性是能确保的，因为一个亚纯函数极点的补集构成一个连通集),因此，我们仍然用符号 Γ 表示。

为了证明所宣称的到亚纯函数的解析延拓，我们需要一个引理，便带展示了Γ函数的一个重要属性。

引理 1.2 若 Re(s) > 0 ,则

(2) $\Gamma(s + 1) = s\Gamma(s)$ 。

其结果是，对于 n = 0, 1 , 2 , ... , 有 Γ(n + 1) = n!

证明：

在有限积分式中按分部积分方法进行积分给到

$\displaystyle \int_{\epsilon}^{1/\epsilon}\frac{d}{dt}(e^{-t} t^{s})dt = -\int_{\epsilon}^{1/\epsilon}e^{-t} t^{s} dt + s\int_{\epsilon}^{1/\epsilon}e^{-t} t^{s-1}dt$ ，

进而，通过令 ε 趋近于 0 ,并注意到，积分式的左边消没(因为 t 趋近于 0 或无穷大时， $(e^{-t} t^{s} \rightarrow 0 )$ , 从而推导同骤然的公式(2) 。现在，只需验证

$\displaystyle \Gamma(1) = \int_{0}^{\infty}e^{-t}dt = \bigg [-e^{-t} \bigg ]_{0}^{\infty} = 1$ ,

接着应用(2)求得Γ(n + 1) = n! 即可。

引理中的公式(2)即是我们所需的给出下列定理证明的全部。

定理 1.3 本节开头针对 Re(s)> 0 所定义的函数 Γ(s) 有一个到 ℂ 上的亚纯函数的解析延拓，其仅有的奇点是位于负整数 s = 0 , -1 ,... 处的极点，则Γ在 s = -n 处的留数(residue)是 $(-n)^{n}/ n!$ 。

证明：

只需将 Γ 延拓到每一个半平面 Re(s)> -m (其中，m ≥ 1 是一个整数)即可。对于 Re(s)> -1 ，我们定义

$\displaystyle F_{1}(s) = \frac{\Gamma(s + 1)}{s}$ 。

因为 Γ(s + 1) 按 Re(s)> -1 是全纯的，我们看到， $F_{1}$ 在那个半平面上是亚纯的，且唯一可能的奇点是位于 s = 0 处的简单极点。此外，若 Re(s)> 0 ，则根据前面的引理，有

$\displaystyle F_{1}(s) = \frac{\Gamma(s + 1)}{s}=\Gamma{(s)}$ 。

因此， $F_{1}$ 将Γ 延拓到半平面 Re(s)> -1 上的一个亚纯函数。我们可以继续按照这种方式，定义与Re(s)> 0 上Γ函数一致的 Re(s)> - m 的亚纯函数 $F_{m}$ 。对于 Re(s)> - m (其中，m ≥ 1 是一个整数)，定义

$\displaystyle F_{m}(s)=\frac{\Gamma{(s+m)}}{(s+m-1)(s+m-2)...s}=\Gamma{(s)}$ 。

则函数按 Re(s)> - m 是全纯的，并且在 s = 0 ，-1 ，-2 ，..., - m + 1 处有简单极点，且具有留数

$\begin{array}{rlc}\displaystyle res_{s=-n}F_{m}(s)&\displaystyle=\frac{\Gamma{(-n+m)}}{(m-1-n)!(-1)(-2)...(-n)} \\ \\ &\displaystyle=\frac{(m-n-1)!}{(m-1-n)!(-1)(-2)...(-n)} \\ \\ &\displaystyle=\frac{(-n)^{n}}{n!} \end{array}$ 。

连续应用引理证明，对于 Re(s)> 0 有 $F_{m}(s)=\Gamma{(s)}$ 根据唯一性特性，这也意味着在 Fk 的定义域上，对于 1 ≤ k ≤ m ,有 $F_{m}=F_{k}$ 。因此，我们获得了预期的Γ 的延拓性。

评注：

我们已经证明，只要 Re(s)> 0 就有 Γ(s + 1) = sΓ(s) 。事实上，根据解析延拓，只要 s ≠ 0，-1 ，-2 ，... ，即，只要 s不是Γ的极点，这个公式仍然成立。这是因为，引理的两侧在Γ的极点的补集中都是全纯的，并且当 Re(s)> 0 时是相等的。事实上，我们可以进一步，并注意到，若 s 是负整数 s = - n (n ≥ 1) ，则引理的两侧都是无限的，此外，

$\displaystyle res_{s=-n}\Gamma{(s+1)}=(-n) res_{s=-n}\Gamma{(s)}$ 。

最后，注意到，当 s = 0 时，我们有 $\displaystyle \Gamma{(1)}=\lim_{s \rightarrow 0}s\Gamma{(s)}$ 。

定理1.3 的另一个等价证明(其本身就很有趣且其思想在后面反复出现)可通过拆分定义于Re(s)> 0 上的 Γ(s)的积分为如下形式而获得：

$\displaystyle \Gamma(s) = \int_{0}^{1}e^{-t} t^{s-1}dt + \int_{1}^{\infty}e^{-t} t^{s-1}dt$ 。

最右边的积分定义了一个复可积函数；此外，按幂级数延拓 $e^{-t}$ 并对其逐项积分给到

$\displaystyle \int_{0}^{1}e^{-t} t^{s-1}dt =\sum_{n=0}^{\infty}\frac{(-n)^{n}}{n!(n+s)}$ 。

因此，

(3) $\displaystyle \Gamma(s) = \sum_{n=0}^{\infty}\frac{(-n)^{n}}{n!(n+s)}+\int_{0}^{\infty}e^{-t} t^{s-1}dt$ ( 对于 Re(s) > 0 )。

最后，这个级数在 ℂ 上定义了一个亚纯函数，其在负整数点具有极点且在 s = - n 处具有留数 $(-n)^{n}/ n!$ 。为了证明这一点，我们按如下的方式论证。对于某个具体的 R > 0 ，我们可以将和拆分成两个部分

$\displaystyle \sum_{n=0}^{\infty}\frac{(-n)^{n}}{n!(n+s)}= \sum_{n=0}^{N}\frac{(-n)^{n}}{n!(n+s)} + \sum_{n=N+1}^{\infty}\frac{(-n)^{n}}{n!(n+s)}$ ，

其中，N是所选择的满足 N > 2R 的整数。第一项有限和定义了一个圆盘 |s| < R 中的亚纯函数，其在预期的点处具有极点且具有正确的留数。第二项和在那个圆盘中一致收敛，因此在那个圆盘上定义了一个全纯函数，因为 n > N > 2R 和 | n + s | ≥ R 意味着

$\displaystyle \bigg |\frac{(-n)^{n}}{n!(n+s)} \bigg | \leq \frac{1}{n!R}$ 。

因为 R 是任意的，我们推断出 (3) 中的属性具有预期的属性。

现在，特别是，关系 (3) 在整个 ℂ上成立。

1.2 Γ函数的更多属性(Further properties of Γ)

下面的恒等式揭示了Γ关于直线 Re(s) = 1/2 的对称性。

定理 1.4 对于所有 s∈ℂ ，有

(4) $\displaystyle \Gamma{(s)}\Gamma{(1-s)}=\frac{\pi}{\sin{\pi{s}}}$ 。

可观察到，函数 Γ(1 - s) 在正整数 s = 1 ，2 ，3 ，... 处具有简单极点，因此Γ(s) Γ(1 - s)是一个在 ℂ上在所有整数处具有简单极点的亚纯函数，函数 $\pi/\sin{\pi{s}}$ 也具有这一特点。

为了证明这个恒等式，只需证明对于 0 < s < 1 也存在这样的恒等式，因为按照解析延拓，上式在整个 ℂ上也成立。

引理 1.5 对于 0 < a < 1 ，有 $\displaystyle \int_{0}^{\infty}\frac{v^{a+1}}{1+v}dv=\frac{\pi}{\sin{\pi}s}$ 。

证明：

我们首先观察到

$\displaystyle \int_{0}^{\infty}\frac{v^{a+1}}{1+v}dv=\int_{-\infty}^{\infty}\frac{e^{ax}}{1+e^{x}}dx$ ，

通过执行变量替换 $v=e^{x}$ 可推导出以上等式。然而，使用周线积分(我们在第3章第2.1节例2中见过)，可求得第二项积分等于 $\pi/\sin{\pi{s}}$ , 正如预期。

为了证明这个定理，我们首先注意到，对于0 < s < 1 ,我们可以写成

$\displaystyle \Gamma{(1 - s)} = \int_{0}^{\infty}e^{-u}u^{-s}du = t\int_{0}^{\infty}e^{-vt}(vt)^{-s}dv$ 。

其中，对于 t > 0 ,我们执行变量替换 vt = u 。则这个技巧给出

$\begin{array}{rlc} \displaystyle \Gamma{(s)}\Gamma{(1-s)}& \displaystyle=\int_{0}^{\infty}e^{-t}t^{s-1}\Gamma(1-s)dt \\ \\ &\displaystyle=\int_{0}^{\infty}e^{-t}t^{s-1}\bigg ( t\int_{0}^{\infty}e^{-vt}(vt)^{-s}dv \bigg ) dt \\ \\ &\displaystyle=\int_{0}^{\infty}\int_{0}^{\infty}e^{-t[1+v]}v^{-s}dvdt \\ \\ &\displaystyle=\int_{0}^{\infty}\frac{v^{-s}}{1+v}dv \\ \\ &\displaystyle=\frac{\pi}{\sin{\pi{(1-s)}}} \\ \\ &\displaystyle=\frac{\pi}{\sin{\pi{s}}} \end{array}$ ，

因此，定理得证。

特别是，通过代入 s = 1/2 并注意到，只要 s > 0 就有 Γ(s) > 0 ，我们求得

$\Gamma(1/2)=\sqrt{\pi}$ 。

我们通过考虑Γ函数的倒数来继续研究Γ函数，结果证明它是一个具有极简属性的复可积函数。

定理 1.6 Γ函数具有下列属性：

(i) 1/Γ(s)是 s 的一个复可积函数，其在 s = 0，-1 ，-2 ，... 处具有简单零点且在其它点处无处消没。

(ii) 1/Γ(s)具递增性

$\displaystyle \bigg |\frac{1}{\Gamma(s)} \bigg | \leq c_{1}e^{c_{2}|s|\log{|s|}}$ 。

因此，对于每一个 ε > 0 ，存在一个边界 c(ε) 使得

$\displaystyle \bigg |\frac{1}{\Gamma(s)} \bigg | \leq c(\epsilon)e^{c_{2}|s|^{1+\epsilon}}$ ，

在这个意义上， 1/Γ(s)是1阶的。

证明：

根据定理，我们可以写成

(5) $\displaystyle \frac{1}{\Gamma(s)} =\Gamma(1-s)\frac{\sin{\pi{s}}}{\pi}$ ，

因此，Γ(1 - s)的简单极点(位于 s = 0，1 ，2 ，...这些点处)被 $\sin{\pi{s}}$ 的简单零点所抵消，因此，因此，1/Γ(s)是在 s = 0，-1 ，-2 ，... 处具有简单零点的复可积函数。

为了证明这个估算结果，我们首先证明,只要 σ = Re(s) 是正数，就有

$\displaystyle \int_{1}^{\infty}e^{-t} t^{\sigma} dt \leq e^{(\sigma+1)\log{(\sigma+1)}}$ 。

选择 n 使其满足 σ ≤ n ≤ σ + 1 。则 $\begin{array}{rlc} \end{array}$

$\begin{array} {rl} \displaystyle \int_{1}^{\infty}e^{-t} t^{\sigma} dt &\displaystyle \leq \int_{0}^{\infty}e^{-t}t^{n}dt \\ \\ &\displaystyle=n! \\ \\ &\displaystyle \leq n^{n} \\ \\ &\displaystyle=e^{n\log{n}} \\ \\ &\displaystyle \leq e^{(\sigma+1)\log{(\sigma+1)}} \end{array}$ 。

因为关系式(3)在整个ℂ上成立，根据(5)我们看到

$\displaystyle \frac{1}{\Gamma{(s)}}=\bigg ( \sum_{0}^{\infty} \frac{(-1)^{n}}{n!(n+1-s)}\bigg)\frac{\sin{\pi{s}}}{\pi}+\bigg (\int_{1}^{\infty}e^{-t}t^{-s}dt \bigg )\frac{\sin{\pi{s}}}{\pi}$ 。

然而，根据我们前面的观察，

$\displaystyle \bigg |\int_{1}^{\infty}e^{-t}t^{-s}dt \bigg | \leq \int_{1}^{\infty}e^{-t}t^{\sigma}dt \leq e^{(|\sigma|+1)\log{(|\sigma|+1}}$ ，

并且，因为 $|\sin{\pi}s | \leq e^{|{\pi}|s}$ (根据sine 函数的Euler 公式) ，我们求得 1/Γ(s)的公式中的第二项受控于 $ce^{(|\sigma|+1)\log{(|\sigma|+1)}}e^{|\pi|s}$ ，而这一项本身又受控于 $c_{1}e^{c_{2}|s|\log{|s|}}$ 。接下来，我们考察这一项

$\displaystyle \sum_{0}^{\infty} \frac{(-1)^{n}}{n!(n+1-s)}\frac{\sin{\pi{s}}}{\pi}$ 。

存在两种情况：Im(s) > 1 和 Im(s) ≤ 1 。在第一种情况下，这个表达式以绝对值形式受控于 $ce^{|\pi|s}$ 。若 Im(s) ≤ 1 ,我们选择 k 作为使得 k – 1/2 ≤ Re(s) < k + 1/2 的整数。则若 k ≥ 1 ,

$\sum_{0}^{\infty} \frac{(-1)^{n}}{n!(n+1-s)}\frac{\sin{\pi{s}}}{\pi}=(-1)^{k-1}\frac{\sin{\pi{s}}}{(k-1)!(k-s)\pi}+\sum_{n \neq k-1}(-1)^{n}\frac{\sin{\pi{s}}}{n!(n+1-s)\pi}$ 。

等式右边的两项均有界；因为第一项 $\sin{\pi{s}}$ 在 s = k 处消没，而第二项的和受控于 $c\sum{1/n!}$ 。

当 k ≤ 0 时，根据我们的假设， $\mathrm{Re}(s) < 1/2$ , 且 $\sum_{0}^{\infty} \frac{(-1)^{n}}{n!(n+1-s)}$ 根据 $c\sum{1/n!}$ 有界而有界，这就推导出了定理的证明。

事实上，1/Γ(s)满足了第5章所讨论的那种增长条件，这种增长条件很自然地导向了函数 1/Γ(s) 的乘积公式，我们接下来探讨这个条件。

定理 1.7 对于所有 $s \in \mathbb{C}$ ， $\displaystyle \frac{1}{\Gamma(s)} = e^{\gamma^s}s\prod_{n=1}^{\infty}(1+\frac{s}{n}) e^{-s/n}$ 。

这个实数 γ 被称为 Euler常数，定义为

$\displaystyle \gamma = \lim_{n \rightarrow \infty}\bigg ( \sum_{n=1}^{N}\frac{1}{n}-\log{N} \bigg )$ 。

这个极限的存在性已经在第I册第8章中的命题3.1中得到证明。但是，在此为了使得证明完整，我们将再次加以论证。观察到

$\sum_{n=1}^{N}\frac{1}{n}-\log{N} =\sum_{n=1}^{N}\frac{1}{n}-\int_{1}^{N}\frac{1}{x}dx= \sum_{n=1}^{N}\int_{n}^{n+1}[\frac{1}{n}-\frac{1}{x}]dx+\frac{1}{N}$ ，

应用中值定理到 f (x) = 1/x ,我们得到

$\displaystyle \bigg | \frac{1}{n}-\frac{1}{x} \bigg | \leq \frac{1}{n^{2}}$ (对于 n ≤ x ≤ n + 1) 。

因此，

$\displaystyle \sum_{n=1}^{N}\frac{1}{n}-\log{N} = \sum_{n=1}^{N-1}a_{n} + \frac{1}{N}$ ，

其中， $|a_{n} | \leq 1/n^{2}$ 。因此， $\sum{a_{n}}$ 收敛，这就证明了定义γ的极限存在。现在，我们可以继续进行 1/Γ 的因式分解的证明。

证明：

根据 Hadamard 因式分解定理，以及 1/Γ 是具有增阶1且在s = 0，-1 ，-2 ，... 处具有简单零点的复可积函数的事实，我们可以将 1/Γ 展开为一个 Weierstrass 积的形式，其形式为

$\displaystyle \frac{1}{\Gamma{(s)}}=se^{As+B}\prod_{n=1}^{\infty}\bigg (1+\frac{s}{n} \bigg ) e^{-s/n}$ 。

此处的A和B是待确定的两个常量。想到，当 s ⟶ 0 时，sΓ(s) ⟶ 1 ，我们求得 B = 0 (或者2πi 的某个整数倍,这样也会得出同样的结果)。置 s = 1 ，根据Γ(1) = 1 这个事实，便产生了

$\begin{array}{rlc} e^{-A}&\displaystyle=\prod_{n=1}^{\infty}\bigg (1+\frac{1}{n}\bigg )e^{-1/n} \\ \\ &\displaystyle=\lim_{n \rightarrow \infty}\bigg (1+\frac{1}{n}\bigg )e^{-1/n} \\ \\ &\displaystyle=\lim_{n \rightarrow \infty}e^{\sum_{n=1}^{\infty}[\log{(1+1/n)}-1/n]} \\ \\ &\displaystyle=\lim_{n \rightarrow \infty}e^{-(\sum_{n=1}^{N}{1/n})+\log{N}+\log{(1+1/N)}} \\ \\ &\displaystyle=e^{-\gamma} \end{array}$ 。

因此，对于某个 k，A = γ + 2πik 。因为，只要 s是实数则Γ(s)是实数，则我们一定有 k = 0，论证完成。

注意，这个证明表明，函数1/Γ(s)在本质上被刻画为具有下列特性的复可积函数：

(i) 在 s = 0，-1，-2 ，... 具有简单零点且在其它点处无处消没，和

(ii) 增阶 ≤ 1 。

注意到， $\sin{\pi{s}}$ 具有一个类似的特征(现在，除去在所有整数点的零点)。然而，当 $\sin{\pi{s}}$ 具有一个更严格的形如 $\sin{\pi{s}}=O(e^{c|s|})$ 的增长估算时，这个估算值(没有指数中的对数)对于 1/Γ(s)不再成立(如练习12所示)。

2. Ζ 函数(The zeta function)

实数 s > 1 的Riemann ζ 函数起初用收敛级数定义为

$\displaystyle \zeta(s) = \sum_{n=1}^{\infty}\frac{1}{n^{s}}$ 。

与Γ函数的情况一样，ζ函数可被延拓到复平面上。存在这个事实的几个证据，我们将在下一节中介绍依赖于ζ 函数方程的方程。

2.1 函数方程和解析延拓(Function equation and analytic continuation)

与处理Γ函数的情况一样，我们首先提供 ζ 函数到 ℂ 中半平面的简单扩展。

命题 2.1 定义ζ(s)的级数对于Re(s) > 1 收敛，且函数ζ在这个半平面上是全纯的。

证明：

若 s = σ + it (其中，σ 和 t 是实数)，则

$\displaystyle |n^{-s} | = |e^{-s\log{n} } | = e^{-\sigma \log{n}} = n^{-\sigma}$ 。

因此，若 σ > 1 + δ > 1 ，定义 ζ 的级数按 $\sum_{n=1}^{\infty}1/n^{1+\delta}$ (其收敛)一致有界。因此，级数 $\sum{1/n^{s}}$ 在每一个半平面 Re(s) > 1 + δ > 1 上一致收敛，故而，级数在 Re(s) > 1 中定义了一个全纯函数。

ζ 到ℂ 中亚纯函数的解析延拓比Γ 函数的情况更为微秒。我们在这里提出的证明将 ζ 与Γ以及另一个重要函数联系了起来。

考虑针对实数 t > 0 所定义的 ζ 函数(已经在第4章中引入)

$\displaystyle \vartheta = \sum_{n=-\infty}^{\infty}e^{-\pi{n}^{2}t}$ 。 (译注：𝜗 的LaTex语法：\vartheta；Unicode: 1D717 。)

应用Poisson求和公式(第4章定理2.4)给出 𝜗 所满足的函数方程，即

$\displaystyle \vartheta(t)= t^{-1/2}\vartheta(1/t)$ 。

我们将需要的 𝜗 的递增和递降是

$\vartheta(t) \leq Ct^{-1/2}$ (当 t ⟶ 0 时)

和

$| \vartheta(t) - 1|\leq Ce^{-\pi{t}}$ (对于某个 C > 0 和所有 t ≥ 1) 。

t 趋近于 0 时的不等式可从函数方程推导出，而t趋近于无穷大时的行为可从以下事实推导出

$\displaystyle \sum_{n \geq 1}e^{-\pi{n^{2}t}} \leq \sum_{n \geq 1}e^{-\pi{nt}} \leq Ce^{-\pi{t}}$ (对于 t ≥ 1 ) 。

现在，我们到了证明 ζ ，Γ 和 𝜗 三者之间的一种重要关系的时候了。

定理 2.2 若 Re(s) > 1，则

$\displaystyle {\pi}^{-s/2}\Gamma(s/2) \zeta(s) = \frac{1}{2} \int_{0}^{\infty}u^{(s/2)-1}\bigg [\vartheta(u)-1 \bigg ]du$ 。

证明：

此证明及更进一步的论证基于观察

(6) $\displaystyle \int_{0}^{\infty}e^{-{\pi}n^{2} u}u^{(s/2)-1}du = {\pi}^{-s/2}\Gamma(s/2)n^{-s}$ (若 n ≥ 1) 。

事实上，如果我们在积分中做变量替换 $u = t/\pi{n}^{2}$ ，则左边成了

$\displaystyle \bigg (\int_{0}^{\infty}e^{-t}t^{(s/2)-1}dt \bigg )({\pi}n^{2})^{-s/2}$ ,

这恰好就是 ${\pi}^{-s/2}\Gamma(s/2)n^{-s}$ 。接下来，注意到

$\displaystyle \frac{\vartheta(u)-1}{2} = \sum_{n=1}^{\infty}e^{-\pi{n}^{2}u}$ 。

在定理陈述之前给出的 𝜗 估计值证明了无限和与积分的互换是合理的，因此，

$\begin{array}{rlc} \displaystyle \frac{1}{2} \int_{0}^{\infty}u^{(s/2)-1}\bigg [\vartheta(u)-1\bigg ]du &\displaystyle=\sum_{n=1}^{\infty}\int_{0}^{\infty}u^{(s/2)-1}e^{-{\pi}n^{2}u}du \\ \\ &\displaystyle= {\pi}^{-s/2}\Gamma(s/2)\sum_{n=1}^{\infty}n^{-s} \\ \\ &\displaystyle= {\pi}^{-s/2}\Gamma(s/2)\zeta(s) \end{array}$ ，

正如所证。

鉴于这一点，我们考虑修改过的 ζ 函数，称其为 𝜉 函数(译注：读作ksee)，这使得ζ 函数表现得更加对称(译注：因此，另命名以示区别)。 Re(s) > 1 的 𝜉 函数定义为

( 7 ) $\displaystyle \xi{(s)}={\pi}^{-s/2}\Gamma(s/2)\zeta(s)$ 。

定理 2.3 𝜉 函数对于Re(s) > 1 是全纯的，且可以解析延拓至整个ℂ上具有在 s = 0点和s = 1点处具有简单极点的亚纯函数。此外，对于所有 s∈ℂ ，有

𝜉(s) = 𝜉(1 - s) 。

证明：

证明的思想就是使用 𝜗 函数方程，即

$\displaystyle \sum_{n=-\infty}^{\infty}e^{-{\pi}n^{2}u} = u^{-1/2}\sum_{n=-\infty}^{\infty}e^{-{\pi}n^{2}u} ( u > 0 )$ 。

则我们可以用 $u^{(s/2)-1}$ 乘以等式的两侧，并尝试对等式按 u 进行积分。不考虑对应 n = 0 的项(其在两个和式中产生无限项)，则一旦我们调用公式(6)，我们会获得预期的等式，并使用变量替换 u ⟼ 1/u 获得类似的公式。实际证明还需要做一些工作，并按如下进行。

令 $\psi(u) = [\vartheta(u) - 1]/2$ 。𝜗 函数的函数方程( $\vartheta(u) = u^{-1/2} \vartheta(1/u)$ )意味着

$\displaystyle \psi(u) = u^{-1/2}\psi(1/u) + \frac{1}{2u^{1/2}} - \frac{1}{2}$ 。

现在，对于 Re(s) > 1 ，根据定理2.2 ，我们有

$\begin{array}{rlc} \displaystyle{\pi}^{-s/2}\Gamma(s/2)\zeta(s) &\displaystyle= \int_{0}^{\infty}u^{(s/2)-1}\psi(u)du \\ \\ &\displaystyle= \int_{0}^{1}u^{(s/2)-1}\psi(u)du + \int_{1}^{\infty}u^{(s/2)-1} \psi(u)du \\ \\ &\displaystyle=\int_{0}^{1}u^{(s/2)-1}\bigg [u^{-1/2}\psi(1/u)+1/(2u^{1/2} )-1/2 \bigg ] du + \int_{1}^{\infty}u^{(s/2)-1}\psi(u)du \\ \\ &\displaystyle=\frac{1}{s-1} - \frac{1}{s} + \int_{1}^{\infty}\bigg (u^{(s/2)-1/2}+u^{(s/2)-1}\bigg )\psi(u)du \end{array}$ (只要 Re(s) > 1) 。

因此，

$\displaystyle \xi(s)=\frac{1}{s-1} - \frac{1}{s} + \int_{1}^{\infty}\bigg (u^{(s/2)-1/2}+u^{(s/2)-1}\bigg )\psi(u)du$ 。

由于函数 𝜓 在无穷远处逞指数递降，因此以上的积分定义了一个复可积函数，从而我们推断出 𝜉 有一个到整个 ℂ上具有在 s = 0点和s = 1点处具有简单极点的解析延拓。此外，立即可推断出，若我们用 1 –s 替换 s ，这个积分保持不变，并且 1/(1 - s) – 1/s 这两项的和也保持不变。我们推断出 𝜉(s) = 𝜉(1 - s)，正如所证。

根据这个恒等式，我们已经证明，对于 𝜉 ，我们获得了对 ζ 函数的预期结果：其解析延拓性和函数方程。

定理 2.4 ζ 函数有一个到整个复平面的亚纯延拓，其唯一奇点是位于 s = 1 处的简单极点。

证明：

观察到，(7)提供了ζ 的亚纯延拓，即

$\displaystyle \zeta(s)={\pi}^{s/2}\frac{\xi(s)}{\Gamma(s/2)}$ 。

回顾到，1/Γ(s/2)是在0，-2，-4，...处具有简单零点的复可积函数，因此，𝜉(s)在原点处的简单极点被1/Γ(s/2)的相应的零点所抵消。其结果，ζ的唯一奇点是位于 s = 1 处的简单极点。

现在，我们将介绍一种 ζ 函数的解析延拓的更基础的方法，这种方法很容易导出其在半平面Re(s) > 0 中的扩展。这种方法在研究ζ 在直线 Re(s) = 1 附近增长属性非常有用(在下一章会需要)。其背后的思想在于比较和式 $\sum_{n=1}^{\infty}n^{-s}$ 和积分 $\int_{1}^{\infty}x^{-s}dx$ 。

命题 2.5 存在一个满足估算 $|\delta_{n} (s)|\leq |s|/n^{\sigma+1}$ 的复可积函数序列 $\{\delta_{n}(s) \}_{n=1}^{\infty}$ (其中 s = σ + it)，并使得

(8) $\displaystyle \sum_{1\leq n<N}\frac{1}{n^{s}} - \int_{1}^{N}\frac{dx}{x^{s}} = \sum_{1\leq n<N}\delta_{n} (s)$ (只要N是一个大于1的整数)。

这个命题具有下列的结果。

推论 2.6 对于 Re(s) > 0 , 我们有

$\zeta(s) -\frac{1}{s-1} = H(s)$ ，

其中， $\displaystyle H(s) = \sum_{n=1}^{\infty}\delta_{n} (s)$ 在半平面 Re(s) > 0 中是全纯的。

为了证明这个命题，我们对比 $\sum_{1 \leq n < N}^{}n^{-s}$ 与 $\sum_{1 \leq n < N}^{}\int_{n}^{n+1}x^{-s}dx$ ，并设

(9) $\displaystyle \delta_{n}(s) = \int_{n}^{n+1}\bigg [\frac{1}{n^{s}} -\frac{1}{x^{s}} \bigg ]dx$ 。

将均值定理应用到 $f(x)=x^{-s}$ 便产生

$\displaystyle \bigg [\frac{1}{n^{s}} -\frac{1}{x^{s}} \bigg ] \leq \frac{|s|}{n^{\sigma+1}}$ (只要 n ≤ x ≤ n + 1)。

因此， $|\delta_n (s)| \leq |s|/n^{\delta+1}$ ，并且由于

$\displaystyle \int_{1}^{N}\frac{dx}{x^{s}} = \sum_{1 \leq n< N }\int_{n}^{n+1}\frac{dx}{x^{s}}$ ，

因此，命题得证。

转向推论，我们首先假设 Re(s) > 1 。在命题的公式(8)中，我们令N趋近于无穷大，并观察到，根据估算 $|\delta_n (s)| \leq |s|/n^{\delta+1}$ ，我们有级数 $\sum{\delta_{n}(s)}$ 的一致收敛(当 δ > 0时，在任意 Re(s) ≥ δ 的任意半平面中)。由于Re(s) > 1 ，级数 $\sum{n^{-s}}$ 收敛于ζ(s) ，这就证明了当 Re(s) > 1 时的论断。这个一致收敛也表明了，当 Re(s) > 0 时， $\sum{\delta_{n}(s)}$ 是全纯的，并因此表明，ζ(s)是可以扩展到那个半平面上的，并且这个恒等式在那个半平面上仍然成立。

评注：

以上所描述的思想可逐步发展从而产生ζ 到整个复平面上的延拓，如问题2和3所示。给出ζ 的完整的解析延拓的另一个论证在问题15和问题16中概述。

作为对命题的应用，我们可以证明，ζ(s)在直线 Re(s) = 1 附近的增长是“平缓的(mild)。” 回顾到，当 Re(s) > 1 时，我们有 $|\zeta(s)| \leq \sum_{n=1}^{\infty}n^{-\infty}$ ，因此，ζ(s)在任意半平面 Re(s) ≥ 1 + δ ( δ > 0 ) 中是有界的。我们将看到，在直线 Re(s) = 1 上，|ζ(s)|受控于 $|t|^{\epsilon}$ (对于任意ε > 0),且在直线附近的增长差不了多少。下面的估算不是最优的。事实上，它们非常粗糙，但足以满足以后的需要。

命题 2.7 假设 s = σ + it 且σ，t∈ℝ 。则对于每一个 $\sigma_{0}(0 \leq \sigma_{0} \leq 1)$ 以及对于每一个 ε > 0 , 都存在一个常量 $c_{\epsilon}$ 使得

( i ) $|\zeta(s)| \leq c_{\epsilon} |t|^{1-\sigma_{0}+\epsilon}$ ( 若 $\sigma_{0} \leq \sigma$ 且 |t| ≥ 1)。

( ii ) $|\zeta^{'}(s)| \leq c_{\epsilon}|t|^{\epsilon}$ (若 1 ≤ σ 且 |t| ≥ 1)。

特别是，命题意味着 $\zeta(1 + it) = O(|t|^{\epsilon})$ (当 | t | 趋近于无穷大时)(注：O 记法表示左侧以右侧为界)，同样的估算对于 $\zeta^{'}$ 也成立。对于证明，我们使用推论 2.6 。回顾估算 $|\delta_{n} (s)| \leq |s|/n^{\delta+1}$ 。我们也有估算 $|\delta_{n} (s)| \leq 2/n^{\sigma}$ ，基于由(9)给出的 $\delta_{n}(s)$ 表达式和 $|n^{-s}| = n^{-\delta}$ 和 $|x^{-s}| \leq n^{-\sigma}$ (若 x ≥ n)这个事实可推导出上式。然后我们将这两个 $|\delta_{n} (s)|$ 的估算式通过观察 $A = A^{\delta} A^{1-\delta }$ 结果将其组合在一起，从而获得边界值表达式

$\displaystyle |\delta_{n} (s)| \leq \bigg (\frac{|s|}{n^{\sigma_{0}+1}} \bigg )^{\delta} \bigg ( \frac{2}{n^{\sigma_{0}}} \bigg)^{1-\delta} \leq \frac{2|s|^{\delta}}{n^{\sigma_{0}+\delta}}$ (只要δ ≥ 0 ) 。