• 论文地址：Learning Perturbations to Explain Time Series Predictions
• 代码地址：https://github.com/josephenguehard/time_interpret
• 收录于：PMLR 2023
• 引用格式【GB/T 7714】：Enguehard J. Learning perturbations to explain time series predictions[C]//International Conference on Machine Learning. PMLR, 2023: 9329-9342.

Abstract

解释“基于多变量时间序列数据的预测”的困难在于：不仅要处理多个特征，还要处理时间依赖性。而且根据时间信息的不同，相同的特征可能会对预测产生截然不同的影响。（在多变量时间序列预测上进行解释的难点）

以前的工作使用了基于扰动的显著性方法来解决这个问题，使用可训练的掩码来对输入进行扰动，以发现哪些特征在哪些时间驱动了模型的预测结果。然而，这类方法从静态数据的类似方法中得到启发，引入了固定的扰动，而在时间序列数据上似乎没有什么动机这样做。（原有方法存在的问题）

在这项工作中，我们的目标是通过不仅学习掩码，而且通过学习相关的扰动来解释预测。（本文的做法）

我们的经验表明，学习这些扰动显著提高了在时间序列数据上解释结果的质量。（效果）

1. Introduction

尽管目前已经提出了许多解释神经网络的方法，但在多元时间序列数据上的解释方法的研究还相对不足。然而，这种类型的数据在医疗领域尤其重要，其中的数据可以是带有时间戳的医疗事件列表或生命体征测量值。因此，对于这种时间因素的处理是至关重要的。

目前，针对多元时间序列数据的解释方法研究主要包括：

• RETAIN¹，这是一种基于注意力的模型，可以通过特征和时间来学习这种注意力；
• FIT²，它通过量化预测分布的变化来估计特征随时间的重要性；
• DynaMask³，将基于扰动的方法应用于多元时间序列。
• …

在这项工作中，我们的目标是进一步改进基于扰动的解释方法，以使其适应于多变量时间序列数据。

在 Fong & Vedaldi (2017)⁴ 和 Crabbé & Van Der Schaar (2021)³ 等人的研究中，虽然掩码(mask)是可学习的，但这个掩码引起的扰动是固定的。例如，Fong & Vedaldi (2017)⁴ 根据特征的掩码值用高斯模糊（特征周围数据的加权平均值）替换特征，掩码值越低，模糊量越高。Crabbé & Van Der Schaar (2021)³ 也采用了这种方法，在时间上对数据进行高斯模糊。这种方法对于图像似乎是合理的，其中的信息可以被认为是局部的，这就解释了为什么卷积神经网络(cnn)具有有限的过滤器大小，但在这类数据上仍然表现得很好。然而，多变量时间序列可能具有长期依赖性，这使得使用时间高斯模糊作为扰动不那么明显。

我们可能不想用局部平均值替换被掩盖的特征，而是想用时间更远的数据来替换它。这就需要用可学习的扰动来代替固定的扰动。

2. Background Work

在这一节中，作者介绍了 Fong & Vedaldi (2017)⁴ 和 Crabbé & Van Der Schaar (2021)³ 等人的研究。

3. Method

虽然 Crabbé & Van Der Schaar (2021) 提出的时间扰动是 Fong & Vedaldi (2017) 在计算机视觉环境中定义的扰动的适应，但这些扰动是固定的和局部的。它们实际上要么被定义为移动平均扰动，要么被定义为时间高斯模糊。然而，时间数据通常具有长期依赖性，因此局部信息可能不足以确定特定时间特征的重要性。

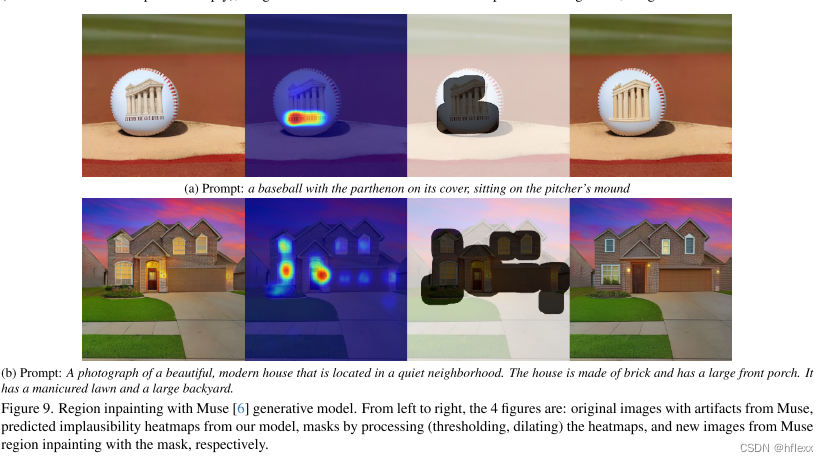
例如，时间数据可以包括重复的模式（周期性）。比如下面这个例子：

在上图中，第1张图为原始数据图像。假设我们的目标是评估第三个尖峰的重要性，这个尖峰很可能不重要，可能只有最后一个尖峰才重要。然而，使用高斯模糊（第2张图）或移动平均（第3张图）会显著改变输入，这可能导致解释方法错误地声明该峰值很重要。另一方面，我们学习到的扰动（第4张图）应该用另一个峰值替换解释的数据，导致输出的差异很小，因此正确地说明该数据不重要。

这种见解需要一个广义的扰动，它可以调整到我们要解释的数据。

第一个想法是通过优化类似于 $arg{\min }_{m\in [0,1{]}^n}\lambda ||m|{|}_1+\mathcal{L}(f(x),f(\Phi (x,m)))$ 的函数，直接学习这个扰动 $\Phi (x)$ ，而不需要掩码。然而，这种方法存在的问题在于，它给了扰动模型太多的自由，会鼓励输出稀疏的解释。

因此我们需要约束扰动算子来解释输入数据的每一部分。我们从 Crabbé & Van Der Schaar (2021) 设计的扰动算子中获得灵感，这些扰动算子通常定义为 $m\times x+(1-m)\times \mu (x)$ ，其中，$\mu (x)$ 定义了扰动的方式。

Crabbé & Van Der Schaar (2021) 设计的扰动算子：
$$\Phi (x,m{)}_{t,i}=\{\begin{array}{l}{m}_{t,i}\times x_{t,i}+(1-m_{t,i})\times {\mu }_{t,i}\\ m_{t,i}\times x_{t,i}+(1-m_{t,i})\times {\mu }_{t,i}^p(1)\\ \frac{{\sum }_{t^{\prime }=1}^T{x}_{t^{\prime },i}\times g_{\sigma (m_{t,i})}(t-t^{\prime })}{{\sum }_{t^{\prime }=1}^T{g}_{\sigma (m_{t,i})}(t-t^{\prime })}\end{array}$$
其中，

${\mu }_{t,i}$ 是 $x_{:,i}$ 在时间 $t$ 前后 $W$ 时间窗口上的平均值。即：
$${\mu }_{t,i}=\frac{1}{2W+1}\sum _{t-W}^{t+W}{x}_{t^{\prime },i}(2)$$
${\mu }_{t,i}^p$ 是 $x_{:,i}$ 在时间 $t$ 前 $W$ 时间窗口上的平均值。即：
$${\mu }_{t,i}^p=\frac{1}{W+1}\sum _{t-W}^t{x}_{t^{\prime },i}(3)$$
$g_{\sigma (m_{t,i})}(t)$ 是时间高斯模糊，其计算方式为：
$$g_{\sigma (m_{t,i})}(t)=exp(-\frac{t^2}{2{\sigma }^2});\sigma (m)={\sigma }_{max}(1-m)(4)$$

在这项工作中，我们提出用神经网络 (NN) 来代替上述这些固定的扰动函数 (1)(2)(3)，并结合掩码来进行训练。因此，我们的扰动定义为：
$$\Phi (x,m)=m\times x+(1-m)\times NN(x)(5)$$
其中，$0⩽m⩽1$

在实践中，我们将模型 $NN(x)$ 定义为 x t , i , t ∈ { 1 , . . . , T } x_{t,i},t\in \{1,...,T\} xt,i​,t∈{1,...,T} 的加权和，因此我们选择双向GRU模型⁵来定义这个神经网络。

在实验中，我们还将双向GRU模型和单向GRU模型进行了对比，单向GRU模型的效果更接近于 Crabbé & Van Der Schaar (2021) 中的 ${\mu }_{t,i}^p$ 。

和 Crabbé & Van Der Schaar (2021) 类似，我们旨在掩盖尽可能多的数据，同时保持与原始数据尽可能接近的预测。因此，我们的优化目标为：
$$arg\underset{m,\Theta \in NN}{\min }\lambda ||m|{|}_1+\mathcal{L}(f(x),f(\Phi (x,m))(6)$$
其中，$\Theta$ 表示神经网络的参数，$\mathcal{L}$ 表示原始预测与扰动预测之间的损失（在分类任务中可以是交叉熵，回归任务中可以是均方误差）。

这个目标函数存在的一个问题是，神经网络可能会倾向于生成更接近于 $x$ 的扰动结果 $NN(x)$ 。如果 $m=0$ ，则 $\Phi (x,m)\approx x$ （几乎没有进行扰动），此时目标函数(6)的取值趋近于0。为了防止这种行为，我们将公式(6)修改为：
$$arg\underset{m,\Theta \in NN}{\min }{\lambda }_1||m|{|}_1+{\lambda }_2||NN(x)|{|}_1+\mathcal{L}(f(x),f(\Phi (x,m))(7)$$
在公式(7)中，我们设置了两个正则化项：$||m|{|}_1$ 和 $||NN(x)|{|}_1$ 。结合扰动公式 $\Phi (x,m)=m\times x+(1-m)\times NN(x)$ 可以看出：

• $m$ 越小，$\Phi (x,m)$ 生成的扰动样本越接近于 $NN(x)$ ，即正则化项 $||m|{|}_1$ 诱导$\Phi (x,m)$ 生成的扰动样本接近于 $NN(x)$ ；
• $NN(x)$ 越小，$\Phi (x,m)$ 生成的扰动样本越接近于0（无信息），即正则化项 $||NN(x)|{|}_1$ 诱导$\Phi (x,m)$ 生成的扰动样本接近于0（无信息）；
• 而公式(7)中的损失函数 $\mathcal{L}$ 则诱导 $f(\Phi (x,m)$ 和 $f(x)$ 尽可能接近。

三者相互制约。

4. Experiments

作者在两个数据集上进行了实验：使用隐马尔可夫模型生成的合成数据集³ 和 真实数据集MIMIC-III⁶。

4.1 Hidden Markov model experiment

作者按照 Crabbé & Van Der Schaar (2021) 的做法，使用2状态隐马尔可夫模型生成1000个时间序列（具体做法可参考 Crabbé & Van Der Schaar (2021) 论文细节³），并训练一个单层GRU模型来根据 $x_t$ 预测对应的 $y_t$ 。

当知道该数据集的真实显著特征时，可以通过比较每种方法产生的显著特征与基础事实之间的相似性来评估我们的解释方法。和 Crabbé & Van Der Schaar (2021) 的做法相同，作者也使用了精确率曲线下面积 (AUP)、召回率曲线下面积 (AUR)、信息量 ($I_M(A)$) 和 掩码熵 ($S_M(A)$) 来作为评估指标。表1是实验结果。

实验结果表明，尽管我们的方法在AUP方面的表现略低于一些基线，但在其他指标上，它的表现明显优于所有其他方法。特别是，虽然它在AUP方面略优于DynaMask，但它在AUR、信息量和掩码熵方面明显产生了更好的结果。

此外，作者还对比了 ${\lambda }_1$ 和 ${\lambda }_2$ 的不同取值对实验结果的影响：

从实验结果中可以看出，

• 当 ${\lambda }_1$ 接近于1时才能产生较好的实验效果。事实上，${\lambda }_1$ 较小时意味着较低的正则化，因此会保留很多不重要的特征；而当 ${\lambda }_1$ 较大时则会迫使 $m$ 接近于0，从而导致大多数的特征被认为不重要。
• 此外，${\lambda }_2$ 需要至少为1才能迫使 $NN(x)$ 学习到无信息的扰动。

4.2 MIMIC-III experiment

和 Crabbé & Van Der Schaar (2021) 的实验类似，作者在真实数据集 MIMIC-III 上对本文提出的解释方法进行了评估。

MIMIC-III 由重症监护病房(ICU)的患者组成，定期测量一些生命体征和实验室检查结果。这里的任务是根据48小时的数据预测每个病人的住院死亡率，每小时离散。缺失的值是使用以前可用的值来输入的。如果没有先前的特征，则输入标准值。

我们训练了一个隐藏层大小为200的单层GRU模型来预测这个住院死亡率（分类任务），我们的目标是解释这个模型。在这个数据集中，真正的显著特征是未知的，我们需要提供不同的指标来评估我们的方法。

评估方式为：将原始预测 与 特定比例的显著特征被掩盖之后的预测 进行了比较，这里用数据样本 对应特征时间维度上的平均值 来 替换被掩盖的特征，即 ${\overline{x}}_{t,i}=\frac{1}{T}{\sum }_t{x}_{t,i}$ ，其中，$T=48$（小时）。在这里用到的评估指标有：

• Accuracy (Acc) 准确率：我们屏蔽最显著的特征，并使用这些被屏蔽的数据计算结果的准确性。较低的准确率意味着做出准确预测的重要特征被删除了。因此，这个度量越低越好。
• Cross-Entropy (CE) 交叉熵损失：我们掩盖最显著的特征，并计算用这些被掩盖的数据与原始数据做出的预测之间的交叉熵。数值越高，表明预测变化越显著，重要特征被删除。因此，这个度量越高越好。
• Comprehensiveness (Comp) 综合性：我们掩盖最显著的特征，并计算预测类概率与原始类概率相比的平均变化。这个度量越高越好。
• Sufficiency (Suff) 充分性：我们只保留最显著的特征，计算预测类概率相对于原始类概率的平均变化。这个指标越低越好。

作者在 表4（屏蔽了前20%最显著的数据，并将数据替换为对应特征时间维度上的平均值 ${\overline{x}}_{t,i}=\frac{1}{T}{\sum }_t{x}_{t,i}$）和 表5（屏蔽了前20%最显著的数据，并将数据替换为对应特征时间维度上的平均值 ${\overline{x}}_{t,i}=0$）中报告了实验结果：

实验结果表明，我们的方法在每个指标上都明显优于其他方法，无论是使用随时间的平均值还是使用零作为屏蔽数据。这也表明，在解释多元时间序列数据的预测时，使用学习扰动比使用固定扰动更可取。

作者还对比了不同扰动模型的实验效果：

（1）用每个特征随时间的总体平均值替换20%的数据：

（2）用零替换20%的数据：

5. Conclusion

我们的研究结果表明，与现有的方法(包括具有固定扰动的DynaMask方法)相比，使用学习扰动可以产生更好的解释。我们还研究了神经网络对扰动建模的选择，发现在MIMIC-III的住院死亡率任务上，单向GRU比双向GRU效果更好，更稳定。

References

---

1. Choi, E., Bahadori, M. T., Sun, J., Kulas, J., Schuetz, A., and Stewart, W. Retain: An interpretable predictive model for healthcare using reverse time attention mechanism. Advances in neural information processing systems, 29, 2016. ↩︎

2. Tonekaboni, S., Joshi, S., Campbell, K., Duvenaud, D. K., and Goldenberg, A. What went wrong and when?instance-wise feature importance for time-series black box models. Advances in Neural Information Processing Systems, 33:799–809, 2020. ↩︎

3. Crabbé J, Van Der Schaar M. Explaining time series predictions with dynamic masks[C]//International Conference on Machine Learning. PMLR, 2021: 2166-2177. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎

4. Fong, R. C. and Vedaldi, A. Interpretable explanations of black boxes by meaningful perturbation. In Proceedings of the IEEE international conference on computer vision, pp. 3429–3437, 2017. ↩︎ ↩︎ ↩︎

5. Cho K, van Merriënboer B, Bahdanau D, et al. On the Properties of Neural Machine Translation: Encoder–Decoder Approaches[J]. Syntax, Semantics and Structure in Statistical Translation, 2014: 103. ↩︎

6. Johnson, A. E., Pollard, T. J., Shen, L., Lehman, L.-w. H., Feng, M., Ghassemi, M., Moody, B., Szolovits, P., Anthony Celi, L., and Mark, R. G. Mimic-iii, a freely accessible critical care database. Scientific data, 3(1):1–9, 2016. ↩︎