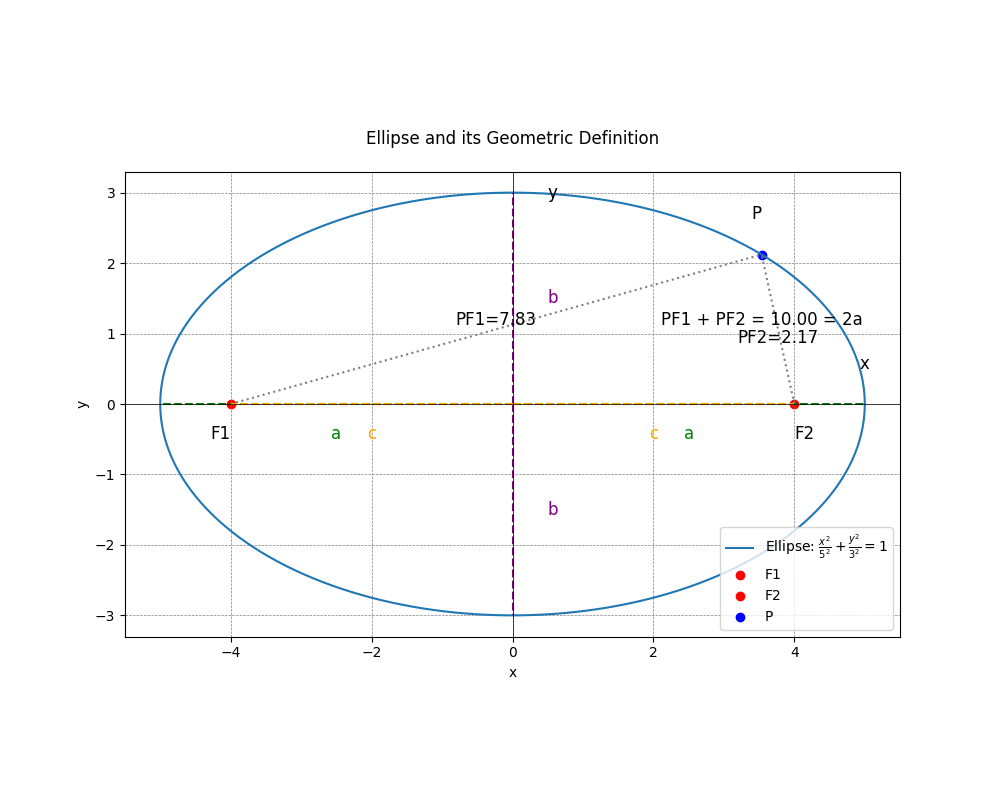
椭圆的几何要素

flyfish

• 椭圆的方程为 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$。

• 长半轴 $a$（绿色虚线）和短半轴 $b$（紫色虚线）。

• 焦点 $F1(-c,0)$（红色点）和 $F2(c,0)$（蓝色点），焦距 $c$（黄色虚线）。

假设我们有一个椭圆，其长轴长度为 $2a$，短轴长度为 $2b$，两个焦点分别位于 $F_1(-c,0)$ 和 $F_2(c,0)$。根据椭圆的定义，椭圆上任意一点到两个焦点的距离之和为常数，并且等于长轴的长度。考虑椭圆上的顶点 $(a,0)$ 和 $(-a,0)$：

• 点 $(a,0)$ 到两个焦点的距离分别为 $$\sqrt{(a+c{)}^2+0^2}$$ 和 $$\sqrt{(a-c{)}^2+0^2}$$，因此有：
  $$\sqrt{(a+c{)}^2}+\sqrt{(a-c{)}^2}=2a$$

$$(a+c)+(a-c)=2a$$

为什么 $c^2=a^2-b^2$

对于椭圆上的任意一点 $P(x,y)$，到两个焦点的距离之和是常数，并且等于椭圆的长轴长度 $2a$$。即
$d(P,F_1)+d(P,F_2)=2a$
其中 $F_1(-c,0)$ 和 $F_2(c,0)$。设 $P(x,y)$ 是椭圆上的任意一点，根据距离公式：
$$d(P,F_1)=\sqrt{(x+c{)}^2+y^2}$$
$$d(P,F_2)=\sqrt{(x-c{)}^2+y^2}$$根据椭圆的定义：
$$\sqrt{(x+c{)}^2+y^2}+\sqrt{(x-c{)}^2+y^2}=2a$$
考虑椭圆上的另一点 $(0,b)$： $(x=0,y=b)$

• 点 $(0,b)$ 到两个焦点的距离分别为
  $$\sqrt{(-c{)}^2+b^2}$$
  $$\sqrt{c^2+b^2}$$，根据椭圆的定义，有：
  $$\sqrt{c^2+b^2}+\sqrt{c^2+b^2}=2a$$

$$2\sqrt{c^2+b^2}=2a$$

$$\sqrt{c^2+b^2}=a$$

两边平方：
$$c^2+b^2=a^2$$

因此，得出结论：
$$c^2=a^2-b^2$$
上图的代码

import matplotlib.pyplot as plt
import numpy as np

# 椭圆的长半轴 a 和短半轴 b
a = 5
b = 3
# 计算焦距 c
c = np.sqrt(a**2 - b**2)

# 创建一个椭圆
theta = np.linspace(0, 2 * np.pi, 1000)
x = a * np.cos(theta)
y = b * np.sin(theta)

# 焦点坐标
F1 = (-c, 0)
F2 = (c, 0)

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']  
plt.rcParams['axes.unicode_minus'] = False  

# 绘制椭圆
plt.figure(figsize=(8, 8))
plt.plot(x, y, label=r'$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$')
plt.scatter(*F1, color='red', label='焦点 F1(-c, 0)')
plt.scatter(*F2, color='blue', label='焦点 F2(c, 0)')

# 标注长半轴 a 和短半轴 b
plt.plot([0, a], [0, 0], 'g--', label='长半轴 a')
plt.plot([0, 0], [0, b], 'm--', label='短半轴 b')
plt.plot([0, -a], [0, 0], 'g--')
plt.plot([0, 0], [0, -b], 'm--')

# 标注焦距 c
plt.plot([0, c], [0, 0], 'y--', label='焦距 c')
plt.plot([0, -c], [0, 0], 'y--')

# 添加图例
plt.legend()

# 设置图形范围
plt.xlim(-6, 6)
plt.ylim(-6, 6)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.gca().set_aspect('equal', adjustable='box')
plt.title("椭圆及其几何要素")
plt.show()