【Python机器学习实战】 | 基于支持向量机（Support Vector Machine, SVM）进行分类和回归任务分析

🎩 欢迎来到技术探索的奇幻世界👨‍💻

📜 个人主页：@一伦明悦-CSDN博客

✍🏻 作者简介： C++软件开发、Python机器学习爱好者

🗣️ 互动与支持：💬评论 👍🏻点赞 📂收藏 👀关注+

如果文章有所帮助，欢迎留下您宝贵的评论，

点赞加收藏支持我，点击关注，一起进步！

引言

svm.SVC是Scikit-learn中用于支持向量机（Support Vector Machine, SVM）分类任务的类。具体来说，svm.SVC实现了基于支持向量的分类器，其核心是在特征空间中找到最佳的超平面来区分不同类别的数据点。

主要参数解释：

C：

正则化参数，控制错误分类样本的惩罚力度。C值越小，容错空间越大，模型可能更简单；C值越大，容错空间越小，模型可能更复杂。

kernel：

核函数的选择，用于将数据从原始特征空间映射到更高维的空间，以便更好地分离不同类别的数据点。
常见的核函数包括线性核（‘linear’）、多项式核（‘poly’）、高斯径向基函数（RBF）核（‘rbf’）、sigmoid核等。

degree（仅在kernel='poly’时有效）：

多项式核函数的阶数。

gamma：

核函数的系数，影响模型的拟合能力。较大的gamma值可以产生更复杂的决策边界，可能导致过拟合。

class_weight：

类别权重的设置，用于处理不平衡类别问题。

probability：

是否启用概率估计。如果设置为True，则会启用概率估计，并在训练过程中计算每个类别的概率。

方法和属性：

fit(X, y)：

训练模型，X是特征数据，y是标签数据。

predict(X)：

对新数据进行预测。

decision_function(X)：

返回每个样本到决策函数的距离。

predict_proba(X)：

返回每个样本预测为各个类别的概率值（仅在probability=True时可用）。

support_：

返回支持向量的索引。

coef_和intercept_：

分别返回决策函数的系数和常数项。

示例用法：
from sklearn import svm
X = [[0, 0], [1, 1]]
y = [0, 1]
clf = svm.SVC()
clf.fit(X, y)
print(clf.predict([[2., 2.]]))
这段代码创建了一个svm.SVC分类器，并用样本X和标签y进行训练。然后，它对新的数据点[[2., 2.]]进行了预测。

总结来说，svm.SVC是一个强大的分类器，通过调整不同的参数（如C、kernel、gamma等），可以实现不同复杂度的分类模型，适用于多种分类问题。

正文

01-分类数据集，并将其可视化

这段代码的作用是生成一个简单的分类数据集，并将其可视化。

具体步骤和功能解释如下：

导入模块：

导入了需要使用的各种Python模块，如numpy用于数值计算，pandas用于数据处理，matplotlib用于绘图，以及一些机器学习相关的模块如sklearn。

设置警告过滤和绘图参数：

warnings.filterwarnings(action='ignore')：设置忽略警告，通常用于屏蔽不影响程序运行的警告信息。
%matplotlib inline：指定在Jupyter Notebook中显示matplotlib绘制的图形。
plt.rcParams：设置matplotlib绘图的一些参数，如中文字体和负号显示问题。

生成分类数据集：

使用make_classification函数生成具有两个特征的分类数据集。
n_samples=N：指定生成样本的数量为100。
n_features=2：每个样本具有2个特征。
n_redundant=0：生成的特征中不包含冗余信息。
n_informative=2：两个特征是信息性的。
class_sep=1：两个类之间的分离度为1。
random_state=1：随机数种子，确保结果可重现。
n_clusters_per_class=1：每个类别内部只有一个簇。
这些参数共同作用，生成了一个具有两个特征和两个类别的分类数据集。

数据集划分：

使用train_test_split函数将生成的数据集划分为训练集和测试集。
train_size=0.85：指定训练集占总数据的85%。
random_state=123：随机数种子，确保划分结果可重现。

数据可视化：

使用matplotlib进行数据的可视化。
markers=['^', 'o']：定义两种不同的标记样式，用于不同类别的数据点。
使用循环结构和条件筛选，分别在训练集和测试集上绘制不同类别的数据点。
plt.scatter函数用于绘制散点图，其中包括了标记样式、颜色、边缘颜色等参数。
plt.title、plt.xlabel、plt.ylabel设置图表标题和坐标轴标签。
plt.grid(True, linestyle='-.')添加网格线，并指定网格线的样式为虚线。

展示图形：

plt.show()显示生成的散点图，展示了训练集和测试集中不同类别的数据点分布情况。

总结：该段代码的主要作用是生成一个包含100个样本观测点的二维分类数据集，并通过散点图展示数据点在特征空间中的分布情况，其中训练集和测试集的不同类别用不同的标记和颜色区分开来。

#本章需导入的模块
import numpy as np
from numpy import random
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
from sklearn.datasets import make_classification,make_circles,make_regression
from sklearn.model_selection import train_test_split,KFold
import sklearn.neural_network as net
import sklearn.linear_model as LM
from scipy.stats import multivariate_normal
from sklearn.metrics import r2_score,mean_squared_error,classification_report
from sklearn import svm
import os

N=100
X,Y=make_classification(n_samples=N,n_features=2,n_redundant=0,n_informative=2,class_sep=1,random_state=1,n_clusters_per_class=1)
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.85, random_state=123)
markers=['^','o']
for k,m in zip([1,0],markers):
    plt.scatter(X_train[Y_train==k,0],X_train[Y_train==k,1],marker=m,s=40)
for k,m in zip([1,0],markers):
    plt.scatter(X_test[Y_test==k,0],X_test[Y_test==k,1],marker=m,s=40,c='r',edgecolors='g')
plt.title("100个样本观测点的分布")
plt.xlabel("X1")
plt.ylabel("X2")
plt.grid(True,linestyle='-.')
plt.show()

运行结果如下图所示：

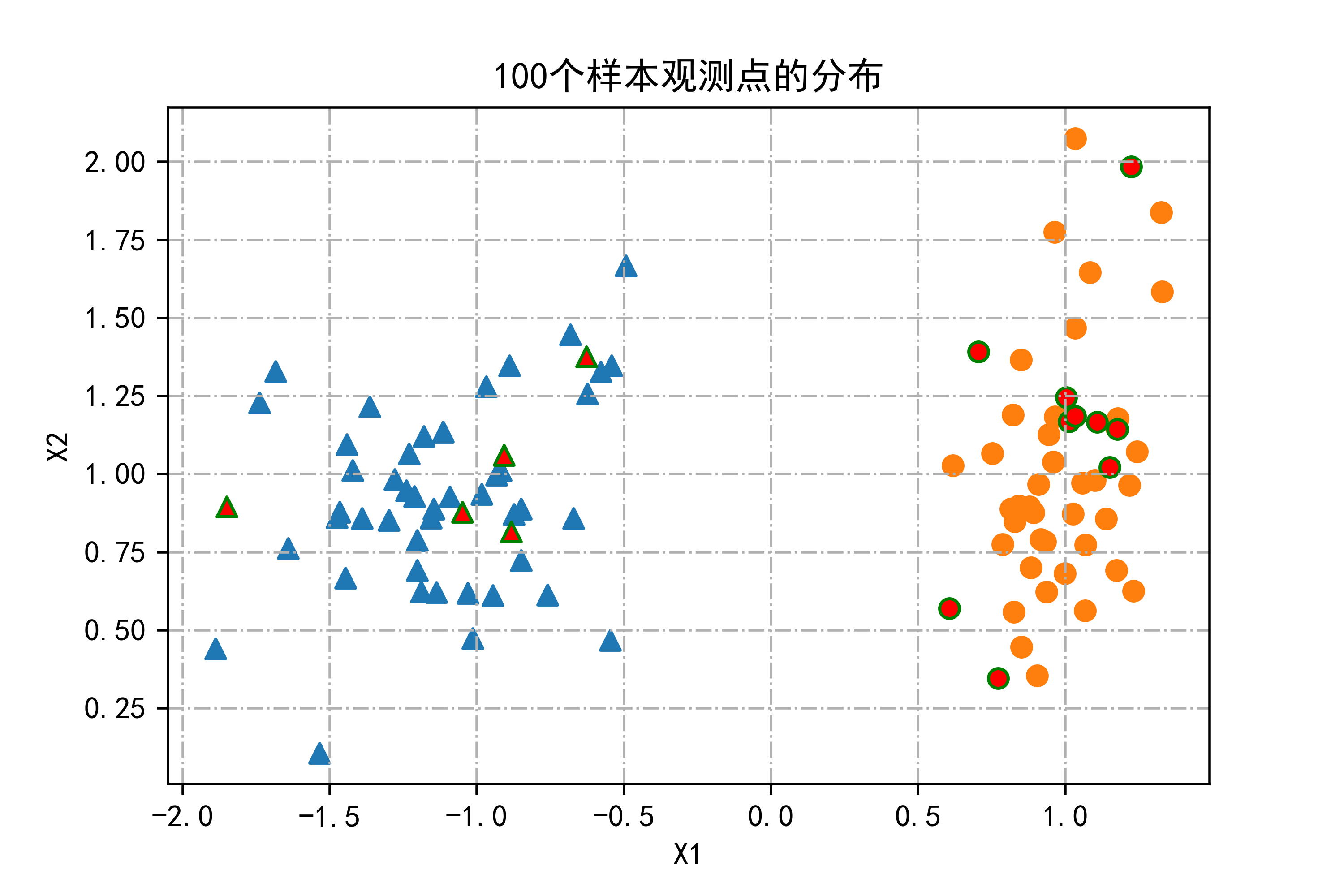
这段代码主要实现了以下功能：

生成网格数据：

使用 np.meshgrid 创建了一个密集的网格点集合 (X1, X2)，覆盖了训练数据集特征空间的范围。这样做是为了后续在整个特征空间内进行预测和可视化。

创建绘图框架：

使用 plt.subplots 创建了一个包含4个子图的图像框架，分布为2行2列，每个子图的大小为 (12, 8)。

循环训练和可视化：

使用循环遍历不同的随机种子 (123, 3000, 0, 20) 和对应的子图位置 (H, L)。
对于每个随机种子，创建一个 MLPClassifier 多层感知器模型 (NeuNet)：
activation='logistic'：指定激活函数为逻辑斯蒂函数。
random_state=seed：设置随机种子，以便结果可复现。
hidden_layer_sizes=(10,)：指定一个包含10个神经元的隐藏层。
max_iter=200：设置最大迭代次数为200。
使用 NeuNet.fit(X_train, Y_train) 对训练集进行训练。

预测和可视化分类结果：

使用训练好的模型 NeuNet 对整个特征空间 (X0) 进行预测，得到预测结果 Y0。
在每个子图中：
根据预测结果将网格点分别用灰色和淡红色表示，以显示模型预测的分类边界。
用不同的标记 ('^' 和 'o') 和颜色 ('r' 和 'g') 分别绘制训练集和测试集的数据点。
添加虚线网格以增强可读性。
设置子图标题，包括当前随机种子和测试误差率 (1 - NeuNet.score(X_test, Y_test)) 的信息。

总结：该段代码通过多次使用不同的随机种子训练 MLPClassifier 模型，并在网格点上绘制模型的分类边界，展示了模型在不同随机种子下的分类效果。每个子图展示了模型对特征空间的不同划分，帮助理解模型在决策边界上的表现。

X1,X2= np.meshgrid(np.linspace(X_train[:,0].min(),X_train[:,0].max(),300),np.linspace(X_train[:,1].min(),X_train[:,1].max(),300))
X0=np.hstack((X1.reshape(len(X1)*len(X2),1),X2.reshape(len(X1)*len(X2),1)))

fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(12,8))
for seed,H,L in [(123,0,0),(3000,0,1),(0,1,0),(20,1,1)]:
    NeuNet=net.MLPClassifier(activation='logistic',random_state=seed,hidden_layer_sizes=(10,),max_iter=200)
    NeuNet.fit(X_train,Y_train)
    #NeuNet.out_activation_  #输出节点的激活函数
    Y0=NeuNet.predict(X0)
    axes[H,L].scatter(X0[np.where(Y0==1),0],X0[np.where(Y0==1),1],c='lightgray')
    axes[H,L].scatter(X0[np.where(Y0==0),0],X0[np.where(Y0==0),1],c='mistyrose')
    for k,m in [(1,'^'),(0,'o')]:
        axes[H,L].scatter(X_train[Y_train==k,0],X_train[Y_train==k,1],marker=m,s=40)
        axes[H,L].scatter(X_test[Y_test==k,0],X_test[Y_test==k,1],marker=m,s=40,c='r',edgecolors='g')
    axes[H,L].grid(True,linestyle='-.')
    axes[H,L].set_title("分类平面(随机数种子=%d,测试误差=%.2f)"%(seed,1-NeuNet.score(X_test,Y_test)))

运行结果如下图所示：

02-线性可分下的支持向量机最大边界超平面分析

这段代码实现了以下功能：

生成数据集：

使用 make_classification 函数生成一个二维特征的分类数据集 X 和对应的标签 Y。数据集具有100个样本，每个样本包括2个特征，是一个线性可分的数据集。

数据集的可视化：

使用 train_test_split 将数据集分割成训练集 (X_train, Y_train) 和测试集 (X_test, Y_test)，其中训练集占85%。
使用 plt.scatter 绘制训练集中的样本点，分别用不同的标记 ('^' 和 'o') 表示两类样本，帮助可视化数据分布。

创建网格数据：

使用 np.meshgrid 创建密集的二维网格 (X1, X2)，覆盖了训练集特征空间的范围。这样做是为了后续在整个特征空间内进行预测和可视化。

训练支持向量机模型：

使用 svm.SVC 创建一个支持向量机分类器 modelSVC，采用线性核函数 (kernel='linear')，设置随机种子 (random_state=123) 和正则化参数 C=2。
使用 modelSVC.fit(X_train, Y_train) 对训练集进行训练，学习得到最大边界超平面以及支持向量的位置。

预测和可视化分类结果：

使用训练好的支持向量机模型 modelSVC 对整个特征空间 (X0) 进行预测，得到预测结果 Y0。
在单个图像中：
根据预测结果将网格点分别用灰色和淡红色表示，以显示模型预测的分类边界。
使用不同的标记 ('^' 和 'o') 和颜色 ('r' 和 'g') 分别绘制训练集和测试集的数据点。
使用蓝色圆圈标记支持向量的位置，并调整其透明度以区分它们。

添加图像元素：

设置图像的标题、坐标轴标签和网格线，增强图像的可读性和解释性。

总结：该段代码展示了如何使用支持向量机处理线性可分的二维数据集。通过训练模型并在特征空间中绘制分类边界和支持向量的位置，帮助理解支持向量机在数据分类中的应用及其决策边界的形成。

#本章需导入的模块
import numpy as np
from numpy import random
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
from sklearn.datasets import make_classification,make_circles,make_regression
from sklearn.model_selection import train_test_split,KFold
import sklearn.neural_network as net
import sklearn.linear_model as LM
from scipy.stats import multivariate_normal
from sklearn.metrics import r2_score,mean_squared_error,classification_report
from sklearn import svm
import os

N=100
X,Y=make_classification(n_samples=N,n_features=2,n_redundant=0,n_informative=2,class_sep=1,random_state=1,n_clusters_per_class=1)

plt.figure(figsize=(9,6))
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.85, random_state=123)
markers=['^','o']
for k,m in zip([1,0],markers):
    plt.scatter(X_train[Y_train==k,0],X_train[Y_train==k,1],marker=m,s=50)
plt.title("训练集中样本观测点的分布")
plt.xlabel("X1")
plt.ylabel("X2")
plt.grid(True,linestyle='-.')
plt.show()   

N=100
X,Y=make_classification(n_samples=N,n_features=2,n_redundant=0,n_informative=2,class_sep=1,random_state=1,n_clusters_per_class=1)
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.85, random_state=123)
X1,X2= np.meshgrid(np.linspace(X_train[:,0].min(),X_train[:,0].max(),500),np.linspace(X_train[:,1].min(),X_train[:,1].max(),500))
X0=np.hstack((X1.reshape(len(X1)*len(X2),1),X2.reshape(len(X1)*len(X2),1)))
modelSVC=svm.SVC(kernel='linear',random_state=123,C=2) #modelSVC=svm.LinearSVC(C=2,dual=False)
modelSVC.fit(X_train,Y_train)
print("超平面的常数项b：",modelSVC.intercept_)
print("超平面系数W：",modelSVC.coef_)
print("支持向量的个数：",modelSVC.n_support_)
Y0=modelSVC.predict(X0)
plt.figure(figsize=(6,4)) 
plt.scatter(X0[np.where(Y0==1),0],X0[np.where(Y0==1),1],c='lightgray')
plt.scatter(X0[np.where(Y0==0),0],X0[np.where(Y0==0),1],c='mistyrose')
for k,m in [(1,'^'),(0,'o')]:
    plt.scatter(X_train[Y_train==k,0],X_train[Y_train==k,1],marker=m,s=40)
    plt.scatter(X_test[Y_test==k,0],X_test[Y_test==k,1],marker=m,s=40,c='r',edgecolors='g')

plt.scatter(modelSVC.support_vectors_[:,0],modelSVC.support_vectors_[:,1],marker='o',c='b',s=120,alpha=0.3)
plt.xlabel("X1")
plt.ylabel("X2")
plt.title("线性可分下的支持向量机最大边界超平面")
plt.grid(True,linestyle='-.')
plt.show()

运行结果如下图所示：

03-广义线性可分下的支持向量机最大边界超平面

这段代码主要包括以下几个部分：

导入必要的模块：

numpy：用于数值计算。
pandas：用于数据处理和分析。
matplotlib.pyplot：用于绘图。
mpl_toolkits.mplot3d：用于绘制3D图形。
warnings：用于控制警告输出。
sklearn 相关模块：包括生成数据集、模型选择、评估指标、支持向量机等。
scipy.stats：用于生成多维正态分布。
os：用于与操作系统进行交互。

生成样本数据和划分训练集、测试集：

使用 make_classification 生成具有分类信息的数据集，包括特征和类别标签。
使用 train_test_split 将数据集划分为训练集和测试集，比例为 0.85：0.15。

绘制训练集样本观测点的分布：

使用不同的标记符号和颜色展示训练集中两类样本点的分布情况。
设置图像标题、坐标轴标签，并显示网格线。
将绘制的图保存为文件，并展示在输出窗口中。

使用支持向量机 (SVM) 模型拟合数据和绘制决策边界：

使用线性核的 SVM 模型，分别设定不同的惩罚参数 C 值。
根据模型预测结果绘制分类边界和支持向量。
在两个子图中展示不同 C 值下的分类效果、支持向量，以及训练集、测试集样本的分布。
设置子图的标题、坐标轴标签，并显示网格线。
将绘制的图保存为文件。

整体上，这段代码主要展示了如何生成分类数据集、划分数据集、利用 SVM 模型进行分类，并通过可视化展示不同参数下的分类效果和支持向量分布。

#本章需导入的模块
import numpy as np
from numpy import random
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
from sklearn.datasets import make_classification,make_circles,make_regression
from sklearn.model_selection import train_test_split,KFold
import sklearn.neural_network as net
import sklearn.linear_model as LM
from scipy.stats import multivariate_normal
from sklearn.metrics import r2_score,mean_squared_error,classification_report
from sklearn import svm
import os

N=100
X,Y=make_classification(n_samples=N,n_features=2,n_redundant=0,n_informative=2,class_sep=1.2,random_state=1,n_clusters_per_class=1)
rng=np.random.RandomState(2)
X+=2*rng.uniform(size=X.shape)
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.85, random_state=1)

plt.figure(figsize=(9,6))
markers=['^','o']
for k,m in zip([1,0],markers):
    plt.scatter(X_train[Y_train==k,0],X_train[Y_train==k,1],marker=m,s=50)
plt.title("训练集中样本观测点的分布")
plt.xlabel("X1")
plt.ylabel("X2")
plt.grid(True,linestyle='-.')
plt.savefig("../4.png", dpi=500) 
plt.show()  

N=100
X,Y=make_classification(n_samples=N,n_features=2,n_redundant=0,n_informative=2,class_sep=1.2,random_state=1,n_clusters_per_class=1)
rng=np.random.RandomState(2)
X+=2*rng.uniform(size=X.shape)
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.85, random_state=1)
X1,X2= np.meshgrid(np.linspace(X_train[:,0].min(),X_train[:,0].max(),500),np.linspace(X_train[:,1].min(),X_train[:,1].max(),500))
X0=np.hstack((X1.reshape(len(X1)*len(X2),1),X2.reshape(len(X1)*len(X2),1)))
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(15,6))
for C,H in [(5,0),(0.1,1)]:
    modelSVC=svm.SVC(kernel='linear',random_state=123,C=C) 
    modelSVC.fit(X_train,Y_train)
    Y0=modelSVC.predict(X0)
    axes[H].scatter(X0[np.where(Y0==1),0],X0[np.where(Y0==1),1],c='lightgray')
    axes[H].scatter(X0[np.where(Y0==0),0],X0[np.where(Y0==0),1],c='mistyrose')
    for k,m in [(1,'^'),(0,'o')]:
        axes[H].scatter(X_train[Y_train==k,0],X_train[Y_train==k,1],marker=m,s=40)
        axes[H].scatter(X_test[Y_test==k,0],X_test[Y_test==k,1],marker=m,s=40,c='r',edgecolors='g')
        
    axes[H].scatter(modelSVC.support_vectors_[:,0],modelSVC.support_vectors_[:,1],marker='o',c='b',s=120,alpha=0.3)
    axes[H].set_xlabel("X1")
    axes[H].set_ylabel("X2")
    axes[H].set_title("广义线性可分下的支持向量机最大边界超平面\n(C=%.1f,训练误差=%.2f)"%(C,1-modelSVC.score(X_train,Y_train)))
    axes[H].grid(True,linestyle='-.')
plt.savefig("../4.png", dpi=500)

运行结果如下图所示

04-广义线性可分下的支持向量机最大边界超平面

这段代码主要包括以下几个部分：

导入必要的模块：

numpy：用于数值计算。
pandas：用于数据处理和分析。
matplotlib.pyplot：用于绘图。
mpl_toolkits.mplot3d：用于绘制3D图形。
warnings：用于控制警告输出。
sklearn 相关模块：包括生成数据集、模型选择、评估指标、支持向量机等。
scipy.stats：用于生成多维正态分布。
os：用于与操作系统进行交互。

生成样本数据和可视化：

使用 make_circles 生成环形结构的数据集，包括特征和类别标签。
创建一个包含两个子图的大图(fig)，其中一个是 3D 散点图，另一个是二维散点图和等高线图。
在 3D 散点图中，根据数据点的位置和类别，使用不同的标记符号和颜色展示样本点的分布情况。
设置 3D 图的 x、y、z 轴标签以及标题。

在二维空间中绘制样本散点图和等高线图：

在第二个子图中，根据样本点的位置和类别，使用不同的标记符号展示样本点的分布情况。
设置二维图的标题、坐标轴标签，并显示网格线。
使用等高线图表示二维样本数据在三维空间中的分布情况。

整体上，这段代码主要展示了如何生成环形结构的数据集，并通过可视化在三维和二维空间中展示样本数据的分布情况。通过这种可视化方式，可以更直观地理解数据的特征和结构。

#本章需导入的模块
import numpy as np
from numpy import random
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
from sklearn.datasets import make_classification,make_circles,make_regression
from sklearn.model_selection import train_test_split,KFold
import sklearn.neural_network as net
import sklearn.linear_model as LM
from scipy.stats import multivariate_normal
from sklearn.metrics import r2_score,mean_squared_error,classification_report
from sklearn import svm
import os

N=100
X,Y=make_circles(n_samples=N,noise=0.2,factor=0.5,random_state=123)
fig = plt.figure(figsize=(20,6))
markers=['^','o']
ax = fig.add_subplot(121, projection='3d')
var = multivariate_normal(mean=[0,0], cov=[[1,0],[0,1]])
Z=np.zeros((len(X),))
for i,x in enumerate(X):
    Z[i]=var.pdf(x)
for k,m in zip([1,0],markers):
    ax.scatter(X[Y==k,0],X[Y==k,1],Z[Y==k],marker=m,s=40)
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.set_zlabel('Z')
ax.set_title('三维空间下100个样本观测点的分布')  

ax = fig.add_subplot(122)
X1,X2= np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),500),np.linspace(X[:,1].min(),X[:,1].max(),500))
X0=np.hstack((X1.reshape(len(X1)*len(X2),1),X2.reshape(len(X1)*len(X2),1)))
Z=np.zeros((len(X0),))
for i,x in enumerate(X0):
    Z[i]=var.pdf(x)
for k,m in zip([1,0],markers):
    ax.scatter(X[Y==k,0],X[Y==k,1],marker=m,s=50)
ax.set_title("100个样本观测点在二维空间中的分布")
ax.set_xlabel("X1")
ax.set_ylabel("X2")
ax.grid(True,linestyle='-.')
contour = plt.contour(X1,X2,Z.reshape(len(X1),len(X2)),[0.12],colors='k')
#ax.clabel(contour,fontsize=10,colors=('k'))  #等高线上标明z（即高度）的值

运行结果如下图所示

总结

支持向量机（Support Vector Machine，SVM）是一种用于分类和回归分析的监督学习模型。以下是支持向量机的总结要点：

原理：

SVM的核心思想是找到一个最优的超平面，将不同类别的样本点分开，并使得两个类别的支持向量到超平面的距离最大化。
SVM在特征空间中寻找一个最优的划分超平面，最大化间隔（Margin），同时引入核技巧进行非线性分类。

优点：

可用于解决线性和非线性分类问题。
在高维空间中有效，适用于特征维度较高的数据集。
泛化能力较强，对过拟合的控制比较好。

缺点：

对大规模样本数据的训练耗时较长，不适用于数据量较大的情况。
对噪声敏感，数据集中存在噪声会影响模型性能。
需要调节核函数和正则化参数，选择合适的参数对模型性能影响较大。

应用：

SVM广泛应用于文本分类、图像识别、生物信息学、医学影像分析等领域。
在实践中，SVM被用于二分类、多分类，以及回归等任务。

核心概念：

支持向量（Support Vectors）：训练数据集中距离超平面最近的样本点。
超平面（Hyperplane）：在特征空间中将不同类别样本点分开的分界线。
间隔（Margin）：支持向量到超平面的距离。

SVM变种：

支持向量回归（Support Vector Regression，SVR）：用于回归问题。
核支持向量机（Kernel SVM）：用于处理非线性分类问题。
多类别SVM：通过一对一（One vs One）或一对其余（One vs Rest）策略处理多类别分类问题。

总的来说，支持向量机是一种强大的机器学习算法，具有良好的分类性能和泛化能力，适用于多种领域的分类和回归任务。在实际应用中，需要合理选择参数、优化模型，并根据具体问题调整算法以提高模型性能。