有时我们想在层的输出端放置一个阈值函数。这可能出于多种原因。其中之一是我们想将激活总结为二进制值。这种激活的二值化在自编码器中很有用。

然而，阈值化在反向传播过程中会带来问题：阈值函数的导数为零。这种梯度的缺乏导致我们的网络无法学习任何东西。为了解决这个问题，我们可以使用直通估计器 (STE：Straight Through Estimator)。

NSDT工具推荐： Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 

1、什么是直通估计器？

假设我们想使用以下函数将层的激活二值化：

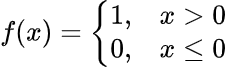
此函数将为每个大于 0 的值返回 1，否则将返回 0。

如前所述，此函数的问题在于其梯度为零。为了解决这个问题，我们将在反向传递中使用直通估计器。

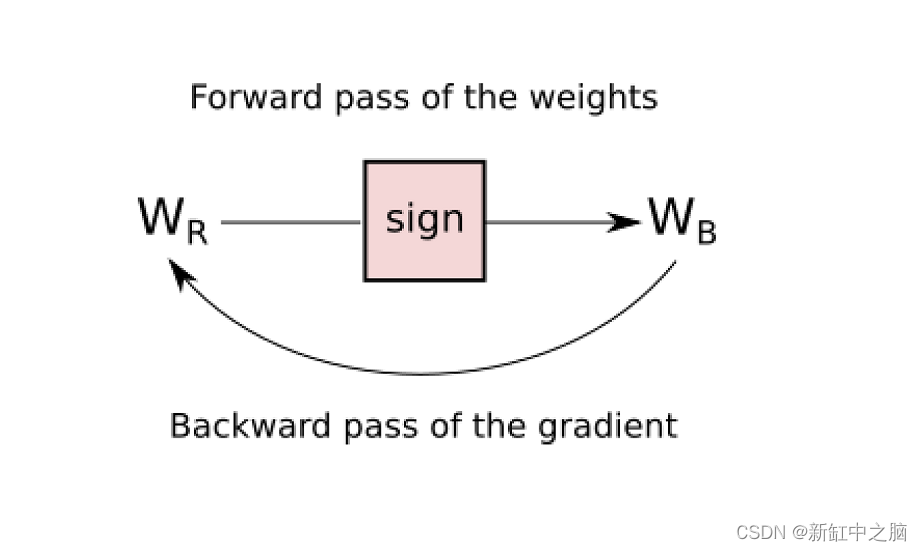
直通估计器顾名思义就是它估计函数的梯度。具体来说，它忽略阈值函数的导数，并将传入的梯度传递，就好像该函数是恒等函数一样。下图有助于更好地解释它：

你可以看到在反向传递中如何绕过阈值函数。就是这样，这就是直通式估计器的作用。它使阈值函数的梯度看起来像恒等函数的梯度。

2、直通估计器的PyTorch 实现

截至目前，PyTorch 的 API 中尚未包含 STE 的实现。因此，我们必须自己实现它。为此，我们需要创建一个 Function 类和一个 Module 类。Function 类将包含 STE 的前向和后向功能。Module 类是创建和使用 STE Function 对象的地方。我们将在我们的神经网络中使用 STE Module。

以下是 STE Function 类的实现：

class STEFunction(torch.autograd.Function):
    @staticmethod
    def forward(ctx, input):
        return (input > 0).float()

    @staticmethod
    def backward(ctx, grad_output):
        return F.hardtanh(grad_output)

PyTorch 让我们可以定义具有前向和后向功能的自定义自动求导函数。这里我们为直通式估算器定义了一个自动求导函数。在前向传递中，我们希望将输入张量中的所有值从浮点转换为二进制。在后向传递中，我们希望传递传入的梯度而不对其进行修改。这是为了模仿恒等函数。不过，这里我们对传入的梯度执行 F.hardtanh 操作。此操作将梯度限制在 -1 和 1 之间。我们这样做是为了让梯度不会变得太大。

现在，让我们实现 STE 模块类：

class StraightThroughEstimator(nn.Module):
    def __init__(self):
        super(StraightThroughEstimator, self).__init__()

    def forward(self, x):
            x = STEFunction.apply(x)
            return x

你可以看到，我们在 forward 函数中使用了我们定义的 STE 函数类。要使用 autograd 函数，我们必须将输入传递给 apply 方法。现在，我们可以在神经网络中使用此模块。

使用 STE 的常见方法是在自编码器的瓶颈层内。以下是此类自编码器的实现：

class Autoencoder(nn.Module):
    def __init__(self):
        super(Autoencoder, self).__init__()
        
        self.encoder = nn.Sequential(
            nn.Conv2d(1, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)),
            nn.ReLU(),
            
            nn.Conv2d(64, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)),
            nn.BatchNorm2d(128),
            nn.ReLU(),
            
            nn.Conv2d(128, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)),
            nn.BatchNorm2d(256),
            nn.ReLU(),
            
            nn.Conv2d(256, 512, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)),
            nn.BatchNorm2d(512),
            nn.ReLU(),
            
            StraightThroughEstimator(),
        )
        self.decoder = nn.Sequential(
            nn.ConvTranspose2d(512, 256, kernel_size=(5, 5), stride=(2, 2), padding=(1, 1)),
            nn.BatchNorm2d(256),
            nn.ReLU(),
            
            nn.ConvTranspose2d(256, 128, kernel_size=(5, 5), stride=(2, 2), padding=(1, 1)),
            nn.BatchNorm2d(128),
            nn.ReLU(),
            
            nn.ConvTranspose2d(128, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)),
            nn.BatchNorm2d(64),
            nn.ReLU(),
            
            nn.ConvTranspose2d(64, 1, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)),
            nn.Tanh(),
        )
        
    def forward(self, x, encode=False, decode=False):
        if encode:
            x = self.encoder(x)
        elif decode:
            x = self.decoder(x)
        else:
            encoding = self.encoder(x)
            x = self.decoder(encoding)
        return x

这个自编码器是为 MNIST 数据集制作的。它将 28x28 图像压缩为具有 512 个通道的 1x1 图像。然后将其解码回 28x28 图像。

我将 STE 放在编码器的末尾。它将把接收到的张量的所有值转换为二进制。你可能已经注意到我使用了一个非常规的前向函数。我添加了两个新参数 encode 和 decrypt，它们要么是 True，要么是 False。如果 encode 设置为 True，网络将返回编码器的输出。同样，如果 decrypt 设置为 True，网络需要有效的编码并将其解码回图像。

我在 MNIST 数据集上对自动编码器进行了 5 个 epoch 的训练，并带有 MSE 损失。以下是测试集上的重建：

如你所见，重建效果非常好。STE 可用于神经网络，且性能不会有太大损失。

完整代码如下：

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torch.autograd as autograd
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm

device = 'cuda:0' if torch.cuda.is_available() else 'cpu'
# dataset preparation
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5, ), (0.5, ))
])
trainset = datasets.MNIST('dataset/', train=True, download=True, transform=transform)
testset = datasets.MNIST('dataset/', train=False, download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)
# defining networks
class STEFunction(autograd.Function):
    @staticmethod
    def forward(ctx, input):
        return (input > 0).float()
    @staticmethod
    def backward(ctx, grad_output):
        return F.hardtanh(grad_output)
class StraightThroughEstimator(nn.Module):
    def __init__(self):
        super(StraightThroughEstimator, self).__init__()
    def forward(self, x):
        x = STEFunction.apply(x)
        return x
class Autoencoder(nn.Module):
    def __init__(self):
        super(Autoencoder, self).__init__()
        
        self.encoder = nn.Sequential(
            nn.Conv2d(1, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)),
            nn.ReLU(),
            
            nn.Conv2d(64, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)),
            nn.BatchNorm2d(128),
            nn.ReLU(),
            
            nn.Conv2d(128, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)),
            nn.BatchNorm2d(256),
            nn.ReLU(),
            
            nn.Conv2d(256, 512, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)),
            nn.BatchNorm2d(512),
            nn.ReLU(),
            
            StraightThroughEstimator(),
        )
        self.decoder = nn.Sequential(
            nn.ConvTranspose2d(512, 256, kernel_size=(5, 5), stride=(2, 2), padding=(1, 1)),
            nn.BatchNorm2d(256),
            nn.ReLU(),
            
            nn.ConvTranspose2d(256, 128, kernel_size=(5, 5), stride=(2, 2), padding=(1, 1)),
            nn.BatchNorm2d(128),
            nn.ReLU(),
            
            nn.ConvTranspose2d(128, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)),
            nn.BatchNorm2d(64),
            nn.ReLU(),
            
            nn.ConvTranspose2d(64, 1, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1)),
            nn.Tanh(),
        )
        
    def forward(self, x, encode=False, decode=False):
        if encode:
            x = self.encoder(x)
        elif decode:
            x = self.decoder(x)
        else:
            encoding = self.encoder(x)
            x = self.decoder(encoding)
        return x
net = Autoencoder().to(device)
optimizer = optim.Adam(net.parameters(), lr=0.001, betas=(0.5, 0.999))
criterion_MSE = nn.MSELoss().to(device)
# train loop
epoch = 5
for e in range(epoch):
    print(f'Starting epoch {e} of {epoch}')
    for X, y in tqdm(trainloader):
        optimizer.zero_grad()
        X = X.to(device)
        reconstruction = net(X)
        loss = criterion_MSE(reconstruction, X)
        loss.backward()
        optimizer.step()
    print(f'Loss: {loss.item()}')
# test loop
i = 1
fig = plt.figure(figsize=(10, 10))
for X, y in testloader:
    X_in = X.to(device)
    recon = net(X_in).detach().cpu().numpy()
    if i >= 10:
      break
    fig.add_subplot(5, 2, i).set_title('Original')
    plt.imshow(X[0].reshape((28, 28)), cmap="gray")
    fig.add_subplot(5, 2, i+1).set_title('Reconstruction')
    plt.imshow(recon[0].reshape((28, 28)), cmap="gray")
    i += 2
fig.tight_layout()
plt.show()

---

原文链接：梯度反传直通图解 - BimAnt