🍭 大家好这里是清隆学长 ，一枚热爱算法的程序员

✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解

💻 ACM银牌🥈| 多次AK大厂笔试 ｜ 编程一对一辅导

👏 感谢大家的订阅➕ 和 喜欢💗

📎在线评测链接

https://app5938.acapp.acwing.com.cn/contest/2/problem/OD1067

🌍 评测功能需要 ⇒ 订阅专栏 ⇐ 后私信联系清隆解锁～

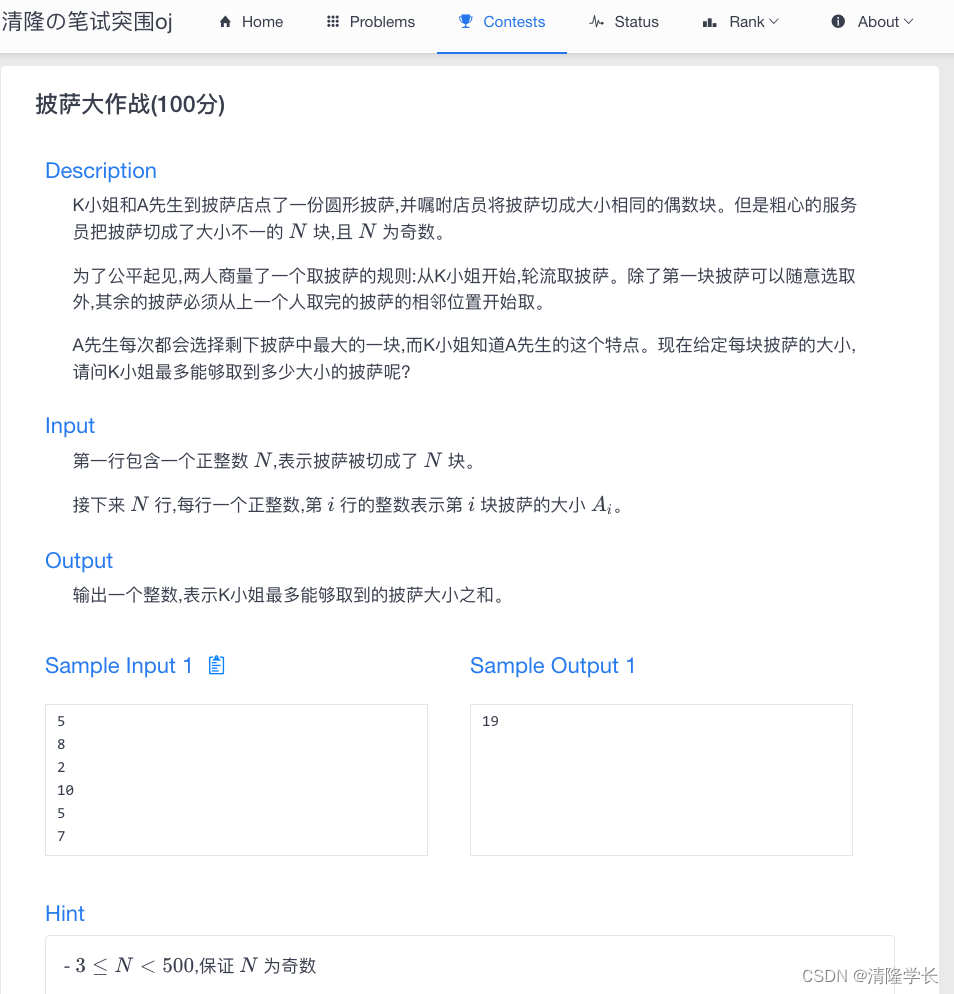
🍓OJ题目截图

🥧 披萨大作战

题目描述

K小姐和A先生到披萨店点了一份圆形披萨,并嘱咐店员将披萨切成大小相同的偶数块。但是粗心的服务员把披萨切成了大小不一的 $N$ 块,且 $N$ 为奇数。

为了公平起见,两人商量了一个取披萨的规则:从K小姐开始,轮流取披萨。除了第一块披萨可以随意选取外,其余的披萨必须从上一个人取完的披萨的相邻位置开始取。

A先生每次都会选择剩下披萨中最大的一块,而K小姐知道A先生的这个特点。现在给定每块披萨的大小,请问K小姐最多能够取到多少大小的披萨呢?

输入格式

第一行包含一个正整数 $N$,表示披萨被切成了 $N$ 块。

接下来 $N$ 行,每行一个正整数,第 $i$ 行的整数表示第 $i$ 块披萨的大小 $A_i$。

输出格式

输出一个整数,表示K小姐最多能够取到的披萨大小之和。

样例输入

5
8
2
10
5
7

样例输出

19

数据范围

• $3\le N<500$,保证 $N$ 为奇数
• $1\le A_i\le 2147483647$

题解

本题可以使用记忆化搜索来解决。

定义 $solve(L,R)$ 表示当前还剩下第 $L$ 块到第 $R$ 块披萨时,K小姐能够取到的最大披萨大小之和。那么答案就是 $max(solve((i+1)\mathrm{mod}N,(i-1+N)\mathrm{mod}N)+A_i)$,其中 $0\le i<N$。

对于函数 $solve(L,R)$,我们可以分情况讨论:

1. 如果 $L=R$,那么只剩下一块披萨,K小姐直接取走,因此 $solve(L,R)=A_L$。

2. 如果 $L\ne R$,那么A先生会取走两端披萨中较大的一块。设 $L^{\prime }$ 和 $R^{\prime }$ 分别表示取走披萨后的左右端点,那么有:

   • 如果 $A_L>A_R$,那么 $L^{\prime }=(L+1)\mathrm{mod}N,R^{\prime }=R$
   • 如果 $A_L\le A_R$,那么 $L^{\prime }=L,R^{\prime }=(R-1+N)\mathrm{mod}N$

   因此 $solve(L,R)=max(A_L+solve(L^{\prime },R),A_R+solve(L,R^{\prime }))$。

为了避免重复计算,我们可以使用记忆化数组 $dp$ 来保存已经计算过的状态。其中 $dp[i][j]$ 表示当前还剩下第 $i$ 块到第 $j$ 块披萨时,K小姐能够取到的最大披萨大小之和。

时间复杂度 $O(N^2)$,空间复杂度 $O(N^2)$。

参考代码

• Python

N = int(input())
A = [int(input()) for _ in range(N)]
dp = [[-1] * N for _ in range(N)]

def solve(L, R):
    if A[L] > A[R]:
        L = (L + 1) % N
    else:
        R = (R - 1 + N) % N
    
    if dp[L][R] != -1:
        return dp[L][R]
    
    if L == R:
        dp[L][R] = A[L]
    else:
        dp[L][R] = max(A[L] + solve((L+1)%N, R), A[R] + solve(L, (R-1+N)%N))
    
    return dp[L][R]

ans = 0
for i in range(N):
    ans = max(ans, solve((i+1)%N, (i-1+N)%N) + A[i])

print(ans)

• Java

import java.util.Scanner;

public class Main {
    static int N;
    static int[] A;
    static int[][] dp;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        N = sc.nextInt();
        A = new int[N];
        for (int i = 0; i < N; i++) {
            A[i] = sc.nextInt();
        }
        dp = new int[N][N];
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                dp[i][j] = -1;
            }
        }
        
        int ans = 0;
        for (int i = 0; i < N; i++) {
            ans = Math.max(ans, solve((i+1)%N, (i-1+N)%N) + A[i]);
        }
        System.out.println(ans);
    }

    static int solve(int L, int R) {
        if (A[L] > A[R]) {
            L = (L + 1) % N;
        } else {
            R = (R - 1 + N) % N;
        }

        if (dp[L][R] != -1) {
            return dp[L][R];
        }

        if (L == R) {
            dp[L][R] = A[L];
        } else {
            dp[L][R] = Math.max(A[L] + solve((L+1)%N, R), A[R] + solve(L, (R-1+N)%N));
        }

        return dp[L][R];
    }
}

• Cpp

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 500;
int n, a[N], dp[N][N];

int solve(int L, int R) {
    if (a[L] > a[R]) {
        L = (L + 1) % n;
    } else {
        R = (R - 1 + n) % n;
    }

    if (dp[L][R] != -1) {
        return dp[L][R];
    }

    if (L == R) {
        dp[L][R] = a[L];
    } else {
        dp[L][R] = max(a[L] + solve((L+1)%n, R), a[R] + solve(L, (R-1+n)%n));
    }

    return dp[L][R];
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    memset(dp, -1, sizeof(dp));

    int ans = 0;
    for (int i = 0; i < n; i++) {
        ans = max(ans, solve((i+1)%n, (i-1+n)%n) + a[i]);
    }

    cout << ans << endl;

    return 0;
}