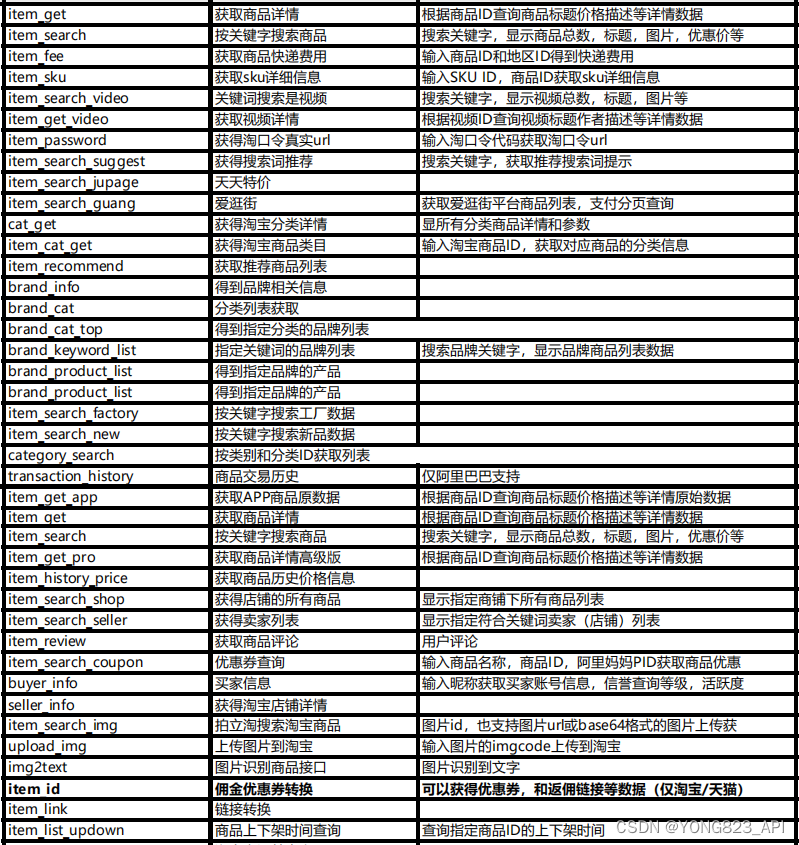
目录
一、向量模式
1、向量模式原理
1.1
1.2
2、向量模式的MATLAB仿真
3、向量模式的FPGA实现
3.1 预处理
3.2 迭代
3.3 结果计算
一、向量模式
1、向量模式原理
已知直角坐标下一点(x,y),如何求该点在极坐标系的坐标(ρ,)?当x和y都为正数时,有
=
,求
的过程即就是求反正切函数的过程。CORDIC算法的思想就是:将向量(x,y)顺时针旋转一定的度数,如果旋转之后纵坐标为0,那么累计旋转的度数就是
,横坐标x的值就是ρ,也就是向量的模长。、
设()为原始坐标,以原点为中心,顺时针旋
之后的坐标为(
),则有如下公式:
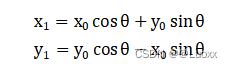
那么每一次旋转的方程都可以这样表示:

上式经过多次迭代之后,就是模长ρ,对于上式迭代有如下化简。
1.1 
前面通过提取公共系数将乘法的次数减少了一半,进一步化简从
入手:除了
为1外,其余
均为无理数,必须进行乘法操作,但乘法其实也是由多个移位器组成,因此如果旋转某个特殊的
值,使得
为简单移位操作,则所有的旋转乘法都可以修改为移位算法。
目前能够将乘法变为移位操作的序列通常都是1/2的n次方或者这些数的组合,例如,计算就可以转化为a右移2位,即a>>2。基于这种思想,可以使各次移位的角度满足
或者
=
,计算出正切值如下表所示。

1.2 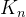
表达式中在迭代时只是一个系数,旋转过程中这个系数与角度
的大小无关且只需关注
趋近于0即可,因此迭代过程中可将的值忽略为1,这样带来的结果是每次旋转后的新坐标模值都比前一次上,具体情况如下图所示。

在仅求解时可以忽略掉系数
,,但求模值时,
每次都会使得横坐标变长,
是一系列固定的值,每次迭代过程中可以忽略,在最终计算模长时统一处理。
每一次都作为乘积因子出现补偿由于旋转作用带来的模长减小,对于确定迭代次数n的方程而言它是一个确定的乘数。
![]()
该乘法多项式的极限为:
![]()
1.3
在每次顺时针旋转后,若纵坐标大于0,说明旋转的度数不够,下一次迭代还要顺时针接着旋转;若纵坐标
小于0,说明旋转的度数太大,下一次迭代就要变为逆时针往回补偿。
所以在向量伪旋转的基础上引入来描述向量旋转的方向,
决定了
的正负,进而表示旋转方向,当
>0时,
顺时针旋转,取1,逆时针则相反。
同时,引入角度累加器参数z用来记录向量的总旋转角度。
综上所述我们得到第i次的迭代方程:

因此n次旋转后的坐标为:

设=0,那么
就是对应向量的相角,
就是对应向量的模值。
2、向量模式的MATLAB仿真
第一步:生成数值表,由数值表,第16次迭代可以达到0.001精度的要求。
| 迭代次数 | 角度 | tan()正切值 | K系数 | 1/K |
| 0 | 45 | 1 | 0.707106781 | 1.414213562 |
| 1 | 26.56505118 | 0.5 | 0.632455532 | 1.58113883 |
| 2 | 14.03624347 | 0.25 | 0.613571991 | 1.629800601 |
| 3 | 7.125016349 | 0.125 | 0.608833913 | 1.642484066 |
| 4 | 3.576334375 | 0.0625 | 0.607648256 | 1.645688916 |
| 5 | 1.789910608 | 0.03125 | 0.60735177 | 1.646492279 |
| 6 | 0.89517371 | 0.015625 | 0.607277644 | 1.646693254 |
| 7 | 0.447614171 | 0.0078125 | 0.607259112 | 1.646743507 |
| 8 | 0.2238105 | 0.00390625 | 0.607254479 | 1.64675607 |
| 9 | 0.111905677 | 0.001953125 | 0.607253321 | 1.646759211 |
| 10 | 0.055952892 | 0.000976563 | 0.607253032 | 1.646759996 |
| 11 | 0.027976453 | 0.000488281 | 0.607252959 | 1.646760193 |
| 12 | 0.013988227 | 0.000244141 | 0.607252941 | 1.646760242 |
| 13 | 0.006994114 | 0.00012207 | 0.607252937 | 1.646760254 |
| 14 | 0.003497057 | 6.10E-05 | 0.607252935 | 1.646760257 |
| 15 | 0.001748528 | 3.05E-05 | 0.607252935 | 1.646760258 |
| 16 | 0.000874264 | 1.53E-05 | 0.607252935 | 1.646760258 |
| 17 | 0.000437132 | 7.63E-06 | 0.607252935 | 1.646760258 |
| 18 | 0.000218566 | 3.81E-06 | 0.607252935 | 1.646760258 |
| 19 | 0.000109283 | 1.91E-06 | 0.607252935 | 1.646760258 |
第二步:开始迭代。
3、向量模式的FPGA实现
3.1 预处理
表中的角度值都为浮点数,在硬件在不易实现,故而将角度做乘法以适当扩大,便于硬件计算。由仿真可知,要达到0.001精度需要16次迭代,也就是说和
最小需要乘以
后做加减,故而在开始16次迭代之前,首先将初始值
和
都算数左移16位,相当于先乘以
,这样可以保证16次迭代中,x和y都一定是整形计算。另外,为了统一起见,这里对所有角度也都乘以
,同样保证角度累加z为整形计算。这样处理后计算的结果也都是乘以
的值,将结果再算数右移16位即得到原始结果。

3.2 迭代
(i+1)次迭代时,判断上一次迭代结果的符号位y[31]的情况,当符号位为0时说明
为正,此时纵坐标大于0,下一次迭代角度要增加,
当符号位为1时相反。以第4次迭代为例。

3.3 结果计算
16次迭代结束后的结果值,趋近0,
为扩展后的模值,
为角度值。
将乘以旋转因子K即可得到模值。16次迭代后的K=0.607252935,在硬件层面做如下化简:
![]()
则模值为:
![]()
FPGA代码链接:基于FPGA的CORDIC算法向量模式实现资源-CSDN文库
Matlab代码链接:基于Matlab的CORDIC算法实现资源-CSDN文库
![【2024最新华为OD-C/D卷试题汇总】[支持在线评测] API集群访问频次统计(100分) - 三语言AC题解(Python/Java/Cpp)](https://img-blog.csdnimg.cn/direct/8ce3e020943a4a1188f6a44036890348.png)