深度学习之计算机视觉

神经网络简介

全连接层和卷积层的根本区别在于权重在中间层中彼此连接的方式。图5.1描述了全连接层或线性层是如何工作的。

在计算机视觉中使用线性层或全连接层的最大挑战之一是它们丢失了所有空间信息，并且就全连接层使用的权重数量而言复杂度太高。例如，当将224像素的图像表示为平面阵列时，我们最终得到的数组长度是150,528(224x224x3通道)。当图像扁平化后，我们失去了所有的空间信息。让我们来看看CNN的化版本是什么样子的，如图5.2 所示。

所有卷积层所做的是在图像上施加一个称为滤波器的权重窗口。在详细理解卷积和其他构建模块之前，先为 MNIST 数据集构建一个简单但功能强大的图像分类器。一旦构建了这个分类器，我们将遍历网络的每个组件。构建图像分类器可分为以下步骤。

获取数据
创建验证数据集
从零开始构建CNN模型
训练和验证模型

MNIST——获取数据

MNIST数据集包含60,000个用于训练的0~9的手写数字图片，以及用于测试集的10,000张图片。PyTorch的torchvision库提供了一个MNIST数据集，它下载并以易于使用的格式提供数据。让我们用MNIST函数把数据集下载到本机，并封装成DataLoader。我们将使用torchvision变换将数据转换成PyTorch张量并进行归一化。下面的代码负责下载数据、把数据封装成 DataLoader以及数据的归一化处理（归一化处理的原因：加快模型的收敛速度、提高模型的精度、增强模型泛化能力）：

# transforms.Normalize((0.1307,), (0.3081))，其中均值（mean）为0.1307，标准差（std）为0.3081。
# 这些参数是在MNIST数据集上的统计结果，用于将图像数据归一化到[0, 1]范围内。
transformation = 
transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081))])
train_dataset = 
datasets.MNIST ('data/', train=True, transform=transformation, download=True)
test_dataset = 
datasets.MNIST('data/', train=False, transform=transformation, download=True)
train_loader =  
torch.utils.data.Dataloader(train_dataset, batch_size=32, shuffle=True)
test_loader = 
torch.utils.data.Dataloader(test_dataset, batch_size=32, shuffle=True)

从零开始构建CNN模型

Conv2d

Conv2d负责在MNIST图像上应用卷积滤波器。让我们试着理解如何在一维数组上应用卷积，然后转向如何将二维卷积应用于图像。我们查看图5.5，将大小为3的滤波器(或内核)conv1d应用于长度为7的张量：

底部框表示7个值的输入张量，连接框表示应用3个卷积滤波器后的输出。在图像的右上角，3个框表示Conv1d 层的权重和参数。卷积滤波器像窗口一样应用，并通过跳过一个值移动到下一个值。要跳过的值称为步幅，并默认设置为1。下面通过写下第一个和最后一个输出的计算来理解如何计算输出值：

Output1->(-0.5209x0.2286)+(-0.0147x2.4488)+(-0.4281x-0.9498)

Output5->(-0.5209x-0.6791)+(-0.0147x-0.6535)+(-0.4281x0.6437)

所以，到目前为止，对卷积的作用应该比较清楚了。卷积基于移动步幅值在输入上应用滤波器，即一组权重。在前面的例子中，滤波器每次移动一格。如果步幅值是2，滤波器将每次移动2格。下面看看PyTorch的实现，来理解它是如何工作的：

conv = nn.Convld(l,l,3,bias=False)
sample = torch.randn(l,l,7)
conv(Variable(sample))
#检查卷积滤波器的权重
conv.weight

还有另一个重要的参数，称为填充，它通常与卷积一起使用。如果仔细地观察前面的例子，大家可能会意识到，如果直到数据的最后才能应用滤波器，那么当数据没有足够的元素可以跨越时，它就会停止。填充则是通过在张量的两端添加0来防止这种情况。下面看一个关于如何填充一维数组的例子。

在图5.6中，我们应用了填充为2步幅为1的Convld层。

让我们看看Conv2d如何在图像上工作。

        在了解Conv2d的工作原理之前，强烈建议大家查看一个非常好的博客(http://setosa.io/ev/image-kernels/)，其中包含一个关于卷积如何工作的现场演示。花几分钟看完演示之后，请阅读下文。
        我们来理解一下演示中发生的事情。在图像的中心框中，有两组不同的数字：一个在方框中表示；另一个在方框下方。在框中表示的那些是像素值，如左边照片上的白色框所突出显示的那样。在框下面表示的数字是用于对图像进行锐化的滤波器(或内核)值。这些数字是精心挑选的，以完成一项特定的工作。在本例中，它用于锐化图像。如前面的例子中一样，我们进行元素级的乘法运算并将所有值相加，生成右侧图像中像素的值。生成的值在图像右侧的白色框中高亮显示。
        虽然在这个例子中内核中的值是精心选择的，但是在CNN中我们不会去精选值而是随机地初始化它们，并让梯度下降和反向传播调整内核的值。学习的内核将负责识别不同的特征，如线条、曲线和眼睛。下面来看图5.7，我们把它看成是一个数字矩阵，看看卷积是如何工作的。

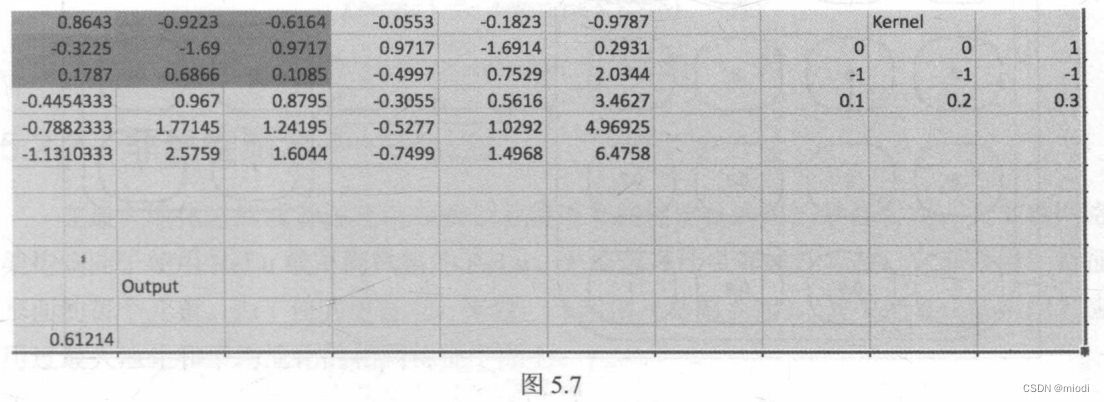
在图5.7中，假设用6x6矩阵表示图像，并且应用大小为3x3的卷积滤波器，然后展示如何生成输出。简单起见，我们只计算矩阵的高亮部分。通过执行以下计算生成输出：

Output->0.86x0+-0.92x0+-0.61x1+-0.32x-1+-1.69x-1+……

Conv2d函数中使用的另一个重要参数是kernel_size，它决定了内核的大小。常用的内核大小有为1、3、5和7。内核越大，滤波器可以覆盖的面积就越大，因此通常会观察到大小为7或9的滤波器应用于早期层中的输入数据。

池化

        通用的实践是在卷积层之后添加池化(pooling)层，因为它们会降低特征平面和卷积层输出的大小。
        池化提供两种不同的功能：一个是减小要处理的数据大小；另一个是强制算法不关注图像位置的微小变化。例如，面部检测算法应该能够检测图片中的面部，而不管照片中面部的位置。
        我们来看看 MaxPool2d的工作原理。它也同样具有内核大小和步幅的概念。它与卷积不同，因为它没有任何权重，只是对前一层中每个滤波器生成的数据起作用。如果内核大小为2x2，则它会考虑图像中2x2的区域并选择该区域的最大值。让我们看看图5.8，它清楚地说明了 MaxPool2d的工作原理。

左侧的框包含特征平面的值。在应用最大池化之后，输出存储在框的右侧。我们写出输出第一行中值的计算代码，看看输出是如何计算的：

Output1 -> Maximum(3,7,2,8) -> 8
Output2 -> Maximum(-1,-8,9,2) -> 9

另一种常用的池化技术是平均池化，需要把average函数替换成maxinum函数。图5.9说明了平均池化的工作原理。

在这个例子中，我们取的是4个值的平均值，而不是4个值的最大值。让我们写出计算代码，以便更容易理解：

Output1 -> Average(3,7,2,8) -> 5
Output2 -> Average(-1,-8,9,2) -> 0.5

非线性激活——ReLU

在最大池化之后或者在应用卷积之后使用非线性层是通用的最佳实践。大多数网络架构倾向于使用ReLu或不同风格的ReLu。无论选择什么非线性函数，它都作用于特征平面的每个元素。为了使其更直观，来看一个示例(见图5.10)，其中把 ReLU 应用到应用过最大池化和平均池化的相同特征平面上：

视图

对于图像分类问题，通用实践是在大多数网络的末端使用全连接层或线性层。我们使用一个以数字矩阵作为输入并输出另一个数字矩阵的二维卷积。为了应用线性层，需要将矩阵扁平化，将二维张量转变为一维的向量。图5.11所示为 view 方法的工作原理。

让我们看看在网络中实现该功能的代码：

x.view(-1,320)

可以看到，view方法将使n维张量扁平化为一维张量。在我们的网络中，第一个维度是每个图像。批处理后的输入数据维度是32x1x28x28，其中第一个数字32表示将有32个高度为28、宽度为28和通道为1的图像，因为图像是黑白的。当进行扁平化处理时，我们不想把不同图像的数据扁平化到一起或者混合数据，因此，传给view函数的第一个参数将指示PyTorch 避免在第一维上扁平化数据。来看看图5.12中的工作原理。

在上面的例子中，我们有大小为2x1x2x2的数据；在应用view函数之后，它会转换成大小为2x1x4的张量。让我们再看一下没有使用参数-1的另一个例子(见图5.13)。

如果忘了指明要扁平化哪一个维度的参数，可能会得到意想不到的结果。所以在这一步要格外小心。

线性层

在将数据从二维张量转换为一维张量之后，把数据传入非线性层，然后传入非线性的激活层。在我们的架构中，共有两个线性层，一个后面跟着ReLU，另一个后面跟着log_softmax，用于预测给定图片中包含的数字。

训练模型

训练模型的过程与之前的狗猫图像分类问题相同。下面的代码片段在提供的数据集上对我们的模型进行训练：

def fit(epoch,model,data_loader,phase='training',volatile=False):
    if phase == 'training':
        model.train()
    if phase == 'validation':
        model.eval()
        volatile=True
    running_loss = 0.0
    running_correct = 0
    for batch_idx,(data,target) in enumerate(data loader):
        if is cuda:
            data,target =data.cuda(),target.cuda()
        data, target = Variable(data,volatile),Variable(target)
    if phase =='training':
        optimizer.zero grad()
    output = model(data)loss =F.nll loss(output,target)
    running loss +=
        F.nll loss(output,target,size average=False).data[0]
    preds = output.data.max(dim=l,keepdim=True)[1]
    running_correct += preds.eq(target.data.view_as(preds)).cpu().sum()
    if phase == 'training':
        loss.backward()
        optimizer.step()
    loss =running_loss/len(data_loader.dataset)
    accuracy =100. * running_correct/len(data_loader.dataset)
    print(f'{phase} loss is {loss:{5}.{2}} and {phase} accuracy is
        {running_correct}/{len(data_loader.dataset)}{accuracy:{10}.{4}}')
    return loss,accuracy

该方法针对 training 和 validation 具有不同的逻辑。使用不同模式主要有两个原因：

在 training 模式中，dropout 会删除一定百分比的值，这在验证或测试阶段不应发生。
对于training 模式，计算梯度并改变模型的参数值，但是在测试或验证阶段不需要反向传播。

上一个函数中的大多数代码都是不言自明的，就如前几章所述。在函数的末尾，我们返回特定轮数中模型的loss和accuracy。
让我们通过前面的函数将模型运行20次迭代，并绘制出training和validation上的loss和 accuracy，以了解网络表现的好坏。以下代码将fit方法在training和validation数据集上运行20次迭代：

model = Net()
if is cuda:
    model.cuda()
optimizer=optim.SGD(model.parameters(),lr=0.01,momentum=0.5)
train_losses , train_accuracy = [],[]
val_losses , val_accuracy = [],[]
for epoch in range(1,20):
    epoch_loss,epoch_accuracy = fit(epoch,model,train_loader,phase='training')
    val_epoch_loss,val_epoch_accuracy = fit(epoch,model,test_loader,phase='validation')
train_losses.append(epoch_loss)
train_accuracy.append(epoch_accuracy)
val_losses.append(val_epoch_loss)
val_accuracy.append(val_epoch_accuracy)

以下代码绘制出了训练和测试的损失值：

plt.plot(range(1,len(train losses)+1),train_losses,'bo',label='training loss')
plt.plot(range(1,len(val losses)+1),val_losses,'r',label='validation loss')
plt.legend()

上述代码生成的图片如图5.14所示。

下面的代码绘制出了训练和测试的准确率：

plt.plot(range(1,len(train accuracy)+1),train accuracy,'bo',label = 'train accuracy')
plt.plot(range(1,len(val accuracy)+1),val accuracy,'r',label = 'val accuracy')
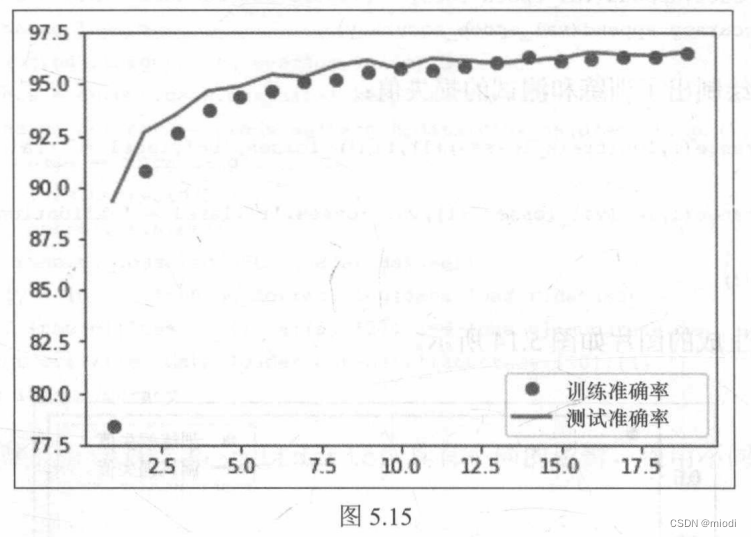
plt.legend()

上述代码生成的图片如图5.15 所示。
在 20轮训练后，我们达到了98.9%的测试准确率。我们使用简单的卷积模型，几乎达到了最先进的结果。让我们看看在之前使用的Dogs vs.Cats数据集上尝试相同的网络架构时会发生什么。我们将使用之前第2章中的数据和MNIST示例中的架构并略微修改。一旦训练好了模型，我们将评估模型，以了解架构表现的优异程度。