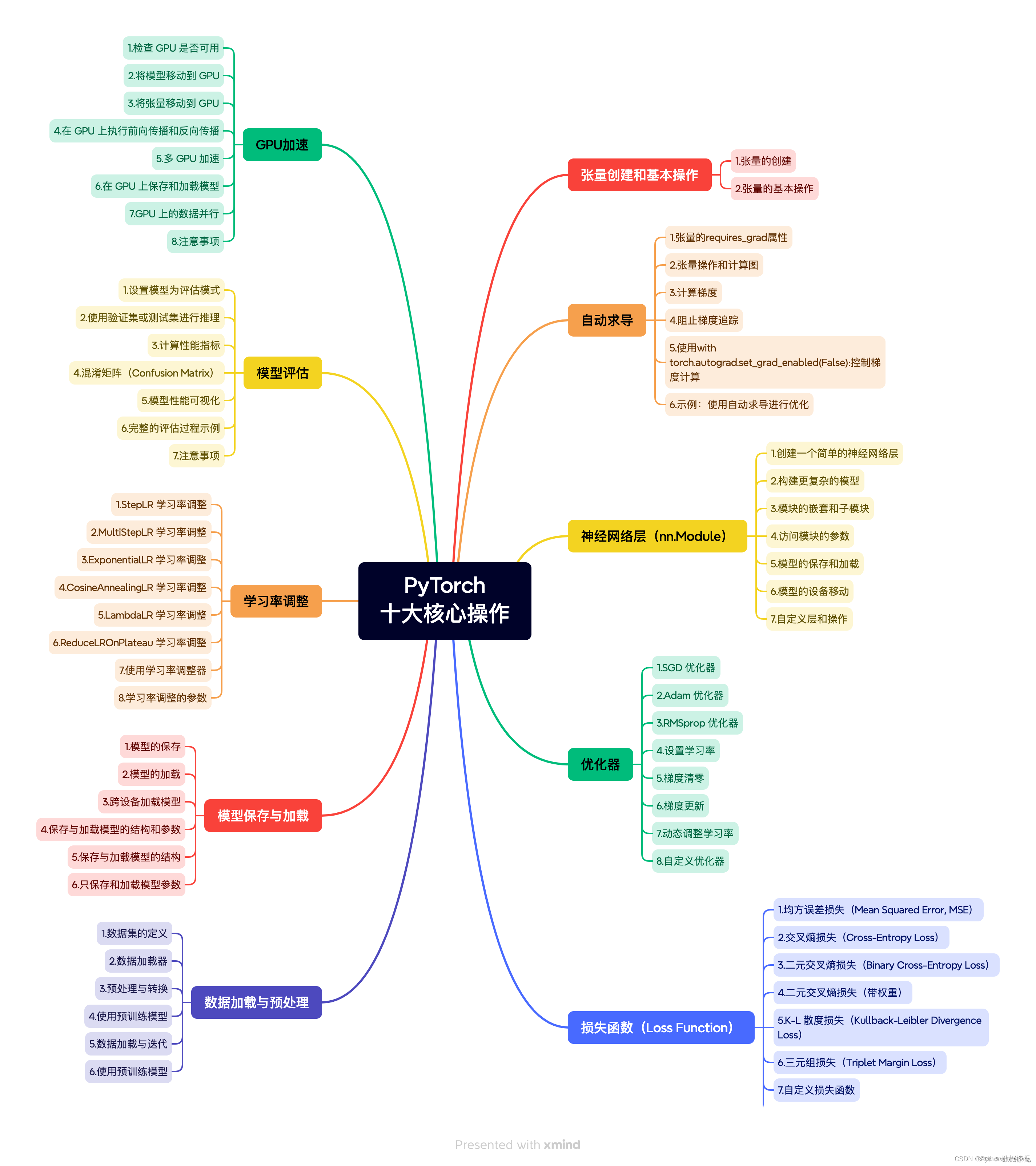
卷积经常用在信号处理中,用于计算信号的延迟累积。假设一个信号发射器每个时刻
t
t
t产生一个信号
x
t
x_t
xt,其信息的衰减率为
w
k
w_k
wk,即在
k
−
1
k-1
k−1个时间步长后,信息为原来的
w
k
w_k
wk倍,时刻
t
t
t收到的信号
y
t
y_t
yt为当前时刻产生的信息
x
t
x_t
xt和以前时刻延迟信息
w
t
−
1
x
t
−
1
+
⋯
+
w
1
x
1
w_{t-1}x_{t-1}+\cdots+w_1x_1
wt−1xt−1+⋯+w1x1的叠加。假设
w
1
=
1
,
w
2
=
1
2
,
w
3
=
1
4
w_1=1,w_2=\frac{1}{2},w_3=\frac{1}{4}
w1=1,w2=21,w3=41也就是
x
1
y
1
=
x
1
x
2
y
2
=
x
2
+
1
2
x
1
x
3
y
3
=
x
3
+
1
2
x
2
+
1
4
x
1
⋮
⋮
\begin{aligned} &x_1&y_1=x_1\\ &x_2&y_2=x_2+\frac{1}{2}x_1\\ &x_3&y_3=x_3+\frac{1}{2}x_2+\frac{1}{4}x_1\\ &\vdots&\vdots \end{aligned}
x1x2x3⋮y1=x1y2=x2+21x1y3=x3+21x2+41x1⋮
因此,时刻
t
t
t(假设前面还有n个信号)收到的信号
y
t
y_t
yt可以记作
y
t
=
w
1
x
t
+
w
2
x
t
−
1
+
⋯
+
w
n
x
t
−
n
+
1
=
∑
k
=
1
n
w
k
x
t
−
k
+
1
\begin{aligned} y_t &=w_1x_t+w_2x_{t-1}+\cdots+w_nx_{t-n+1}\\ &=\sum_{k=1}^nw_kx_{t-k+1} \end{aligned}
yt=w1xt+w2xt−1+⋯+wnxt−n+1=k=1∑nwkxt−k+1
其中
w
k
w_k
wk叫做滤波器(filter) 或卷积核(convolution kernel)
定义
给定一个输入信号序列
x
x
x和滤波器
w
w
w,卷积输出为:
y
t
=
∑
k
=
1
K
w
k
x
t
−
k
+
1
y_t=\sum_{k=1}^Kw_kx_{t-k+1}
yt=k=1∑Kwkxt−k+1
也可记作
y
t
=
x
∗
w
y_t=x\ast w
yt=x∗w,其中
∗
*
∗是卷积符号。要注意卷积核的序列顺序与输入信号序列顺序相反,在运算时需要将卷积核反转。

上图中,下面一行为输入序列 x x x,上面为输出序列 y y y,卷积核为 [ − 1 , 0 , 1 ] [-1,0,1] [−1,0,1],为了计算首先反转卷积核变为 [ 1 , 0 , − 1 ] [1,0,-1] [1,0,−1](或者从第三个开始往前计算,完成后再从开始的第三个再往后三个也就是第六个往前,以此类推),将反转后的卷积核在输入序列上平移得到输出序列。对于长度为 N N N的输入序列 x x x来说,若卷积核长度为 K K K,则输出序列 y y y长度为 N − K + 1 N-K+1 N−K+1
作用
近似微分
将输入序列
x
=
[
x
t
−
1
,
x
t
,
x
t
+
1
]
x=[x_{t-1},x_t,x_{t+1}]
x=[xt−1,xt,xt+1]看作关于某时刻
t
t
t的函数,即
x
(
t
)
=
x
t
x(t)=x_t
x(t)=xt,根据一阶微分定义
x
′
(
t
)
=
x
(
t
+
ϵ
)
−
x
(
t
−
ϵ
)
2
ϵ
x^\prime(t)=\frac{x(t+\epsilon)-x(t-\epsilon)}{2\epsilon}
x′(t)=2ϵx(t+ϵ)−x(t−ϵ)
令
ϵ
=
1
\epsilon=1
ϵ=1可得
x
′
(
t
)
=
x
(
t
+
1
)
−
x
(
t
−
1
)
2
=
1
2
x
(
t
+
1
)
+
0
×
x
t
−
1
2
x
(
t
−
1
)
=
x
∗
w
\begin{aligned} x^\prime(t) &=\frac{x(t+1)-x(t-1)}{2}\\ &=\frac{1}{2}x(t+1)+0\times x_t-\frac{1}{2}x(t-1)\\ &=x\ast w \end{aligned}
x′(t)=2x(t+1)−x(t−1)=21x(t+1)+0×xt−21x(t−1)=x∗w
其中
w
=
[
1
2
,
0
,
−
1
2
]
w=[\frac{1}{2},0,-\frac{1}{2}]
w=[21,0,−21]。因此,当令卷积核
w
=
[
1
2
,
0
,
−
1
2
]
w=[\frac{1}{2},0,-\frac{1}{2}]
w=[21,0,−21]时,可以近似信号序列的一阶微分
此外,根据泰勒公式
x
(
t
+
ϵ
)
=
x
(
t
)
+
x
′
(
t
)
ϵ
+
x
′
′
(
t
)
2
!
ϵ
2
+
O
(
ϵ
3
)
x(t+\epsilon)=x(t)+x^\prime(t)\epsilon+\frac{x^{\prime\prime}(t)}{2!}\epsilon^2+O(\epsilon^3)
x(t+ϵ)=x(t)+x′(t)ϵ+2!x′′(t)ϵ2+O(ϵ3)
因此可得
x
(
t
+
1
)
=
x
(
t
)
+
x
′
(
t
)
+
x
′
′
(
t
)
2
x
(
t
−
1
)
=
x
(
t
)
−
x
′
(
t
)
+
x
′
′
(
t
)
2
\begin{aligned} x(t+1)=x(t)+x^\prime(t)+\frac{x^{\prime\prime}(t)}{2}\\ x(t-1)=x(t)-x^\prime(t)+\frac{x^{\prime\prime}(t)}{2} \end{aligned}
x(t+1)=x(t)+x′(t)+2x′′(t)x(t−1)=x(t)−x′(t)+2x′′(t)
两式相加得
x
(
t
+
1
)
+
x
(
t
−
1
)
=
2
x
(
t
)
+
x
′
′
(
t
)
x
′
′
=
x
(
t
+
1
)
+
x
(
t
−
1
)
−
2
x
(
t
)
=
x
∗
w
\begin{aligned} x(t+1)+x(t-1)&=2x(t)+x^{\prime\prime}(t)\\ x^{\prime\prime}&=x(t+1)+x(t-1)-2x(t)\\ &=x\ast w \end{aligned}
x(t+1)+x(t−1)x′′=2x(t)+x′′(t)=x(t+1)+x(t−1)−2x(t)=x∗w
其中
w
=
[
1
,
−
2
,
1
]
w=[1,-2,1]
w=[1,−2,1]。因此,当令卷积核
w
=
[
1
,
−
2
,
1
]
w=[1,-2,1]
w=[1,−2,1]时,可以近似信号序列的二阶微分
低通滤波/高通滤波
- 高频信息:在信号序列中,局部数值变化剧烈的信息
- 低频信息:在信号序列中,局部数值变化缓慢的信息
对于一个窗口大小为
K
K
K的卷积核,只需要将滤波器中的每一项设置为
1
K
\frac{1}{K}
K1即可检测信号序列中的低频信息。

上图中
K
=
3
K=3
K=3
一般来说,信号序列中的某个信息出现的频率越高,对应的阶数就越高。因此可以用二阶导数(
w
=
[
1
,
−
2
,
1
]
w=[1,-2,1]
w=[1,−2,1])的大小来表示其出现的频率。

对卷积进行扩展
为了更灵活的使用卷积,可以对卷积的过程进行扩展,引入滤波器的滑动步长(Stride)
S
S
S和零填充(Padding)
P
P
P
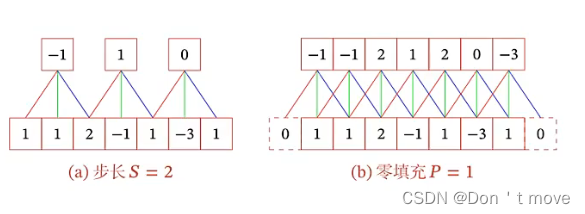
滑动步长是指卷积核在输入序列上每次平移的步长,一般默认滑动步长为1,也就是每次计算完输入序列上的一次卷积后,向前移动一个元素再进行卷积计算,通过增加步长可以减少输出序列的长度。
零填充是指在输入序列的两端各填充
P
P
P个0,这样做可以保证输入序列和输出序列长度相等。对于一个窗口大小为
K
K
K(一般为奇数)的卷积核来说,在输入序列两端各填充
K
−
1
2
\frac{K-1}{2}
2K−1
若输入长度为 M M M,步长为 S S S,卷积核窗口大小为 K K K,零填充为 P P P,则输出长度为 M ′ = M − K + 2 P S + 1 M^\prime=\frac{M-K+2P}{S}+1 M′=SM−K+2P+1
卷积类型可以按照输出长度不同可以分为三类:
- 窄卷积:步长 S = 1 S=1 S=1,两端不补零( P = 0 P=0 P=0),输出长度为 M − K + 1 M-K+1 M−K+1
- 宽卷积:步长 S = 1 S=1 S=1,两端补零( P = K − 1 P=K-1 P=K−1),输出长度为 M + K − 1 M+K-1 M+K−1
- 等宽卷积:步长 S = 1 S=1 S=1,两端补零( P = K − 1 2 P=\frac{K-1}{2} P=2K−1),输出长度为 M M M
早期的文献中,卷积一般默认为窄卷积
目前的文献中,卷积一般默认为等宽卷积
二维卷积
输入序列扩展为二维,对这个二维输入序列进行卷积,一般用于图像处理。
给定图像
X
∈
R
M
×
N
X\in\mathbb{R}^{M\times N}
X∈RM×N和一个滤波器
W
∈
R
U
×
V
W\in\mathbb{R}^{U\times V}
W∈RU×V(
U
≪
M
,
V
≪
N
U\ll M,V\ll N
U≪M,V≪N) ,其卷积为
Y
=
W
∗
X
Y=W\ast X
Y=W∗X
y
i
j
=
∑
u
=
1
U
∑
v
=
1
V
w
u
v
x
i
−
u
+
1
,
j
−
v
+
1
y_{ij}=\sum_{u=1}^U\sum_{v=1}^Vw_{uv}x_{i-u+1, j-v+1}
yij=u=1∑Uv=1∑Vwuvxi−u+1,j−v+1
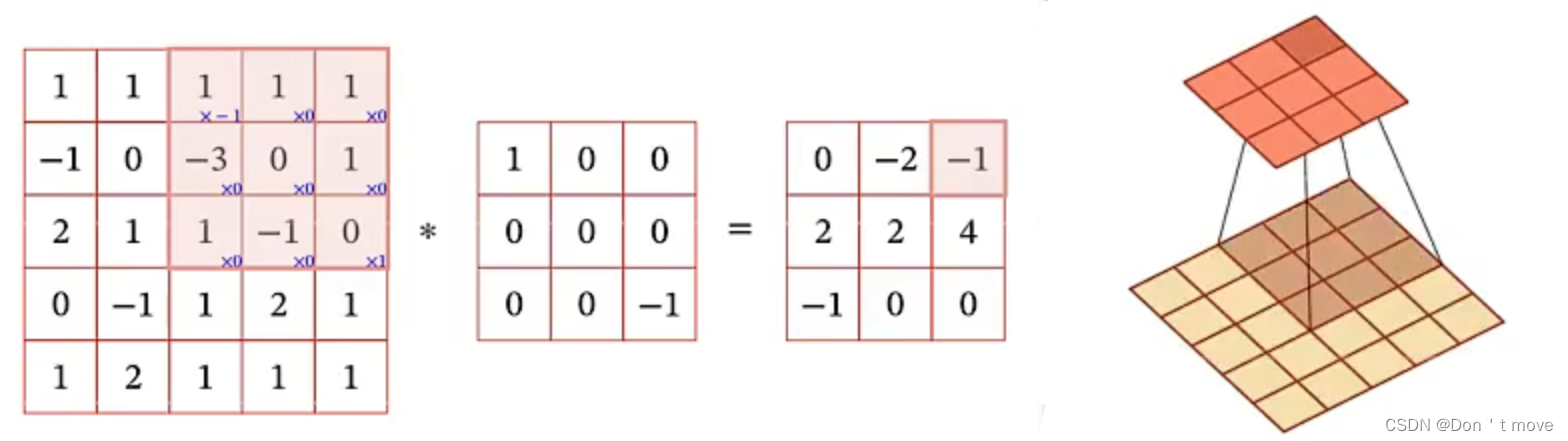
卷积核窗口在输入序列上进行滑动,可以计算出每个位置上的信号,最终得到输出。在计算时仍然要对卷积核进行反转。以上图为例,实际上是计算输入与反转后的卷积核的哈达玛积所有元素的和。
输入与输出大小与一维时规则相同,输出
y
∈
R
(
M
−
U
+
1
)
×
(
N
−
V
+
1
)
y\in\mathbb{R}^{(M-U+1)\times(N-V+1)}
y∈R(M−U+1)×(N−V+1)。同样的也可以用滑动步长和零填充的方法来调整输出矩阵的大小:
-
对于步长为1,零填充0的输入序列,输出为 R ( M − U + 1 ) × ( N − V + 1 ) \mathbb{R}^{(M-U+1)\times(N-V+1)} R(M−U+1)×(N−V+1)
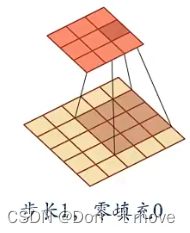
-
对于步长为2,零填充0的输入序列,输出为 R ( M − U 2 + 1 ) × ( N − V 2 + 1 ) \mathbb{R}^{(\frac{M-U}{2}+1)\times(\frac{N-V}{2}+1)} R(2M−U+1)×(2N−V+1)
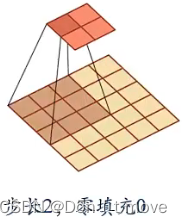
-
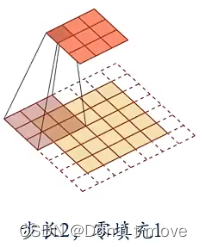
对于步长为1,零填充1的输入序列,输出为 R M × N \mathbb{R}^{M\times N} RM×N

-
对于步长为2,零填充1的输入序列,输出为 R ( M − U + 1 ) × ( N − V + 1 ) \mathbb{R}^{(M-U+1)\times(N-V+1)} R(M−U+1)×(N−V+1)
在图像处理中,可以利用卷积作为特征提取器,设计不同的卷积核来提取图像的不同特征。
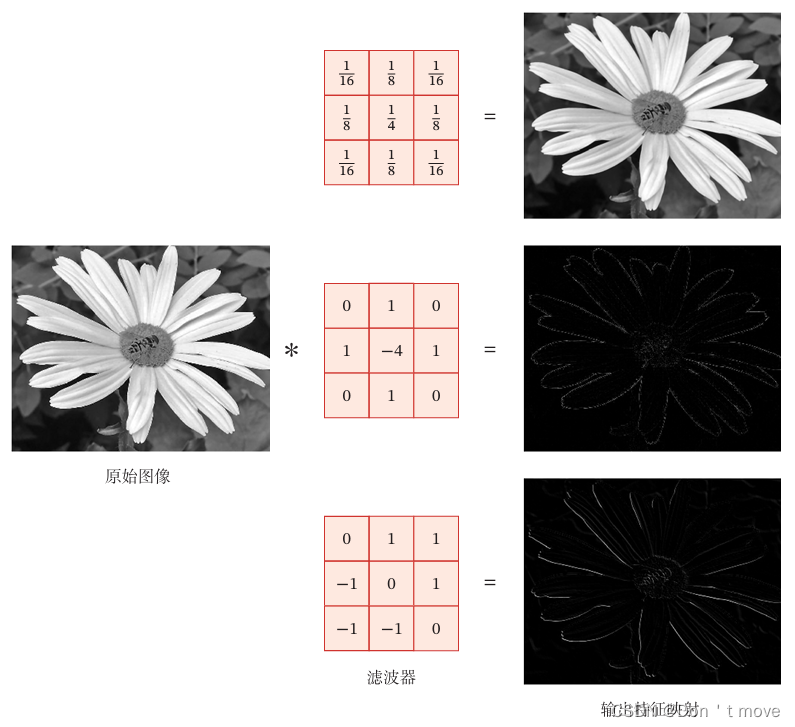
如上图,通过第一个卷积核(高斯卷积核)可以去除图像中的噪声(用周围点的信息平均中间不一样点的信息),使图像更加平滑;通过第二个卷积核,可以提取图像的边缘特征(上下左右信息的和减去中间信息,即提取图像中的高频信息);第三个卷积核可以提取图像对角线上的边缘特征(右上角图像信息减去左下角图像信息)