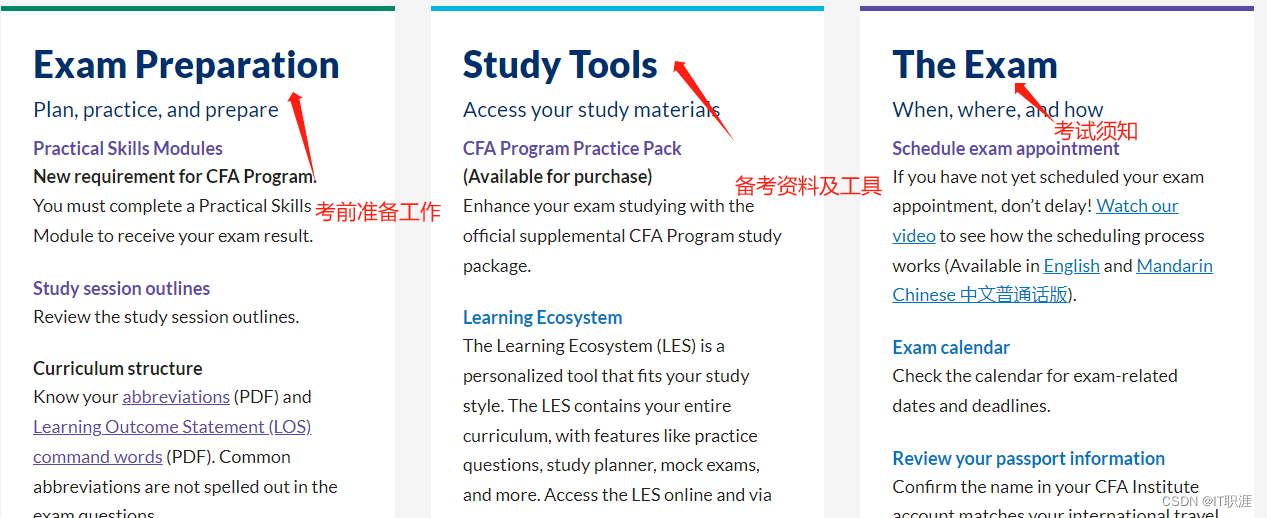
GDUFE
在期末前再刷一次链表题 ~
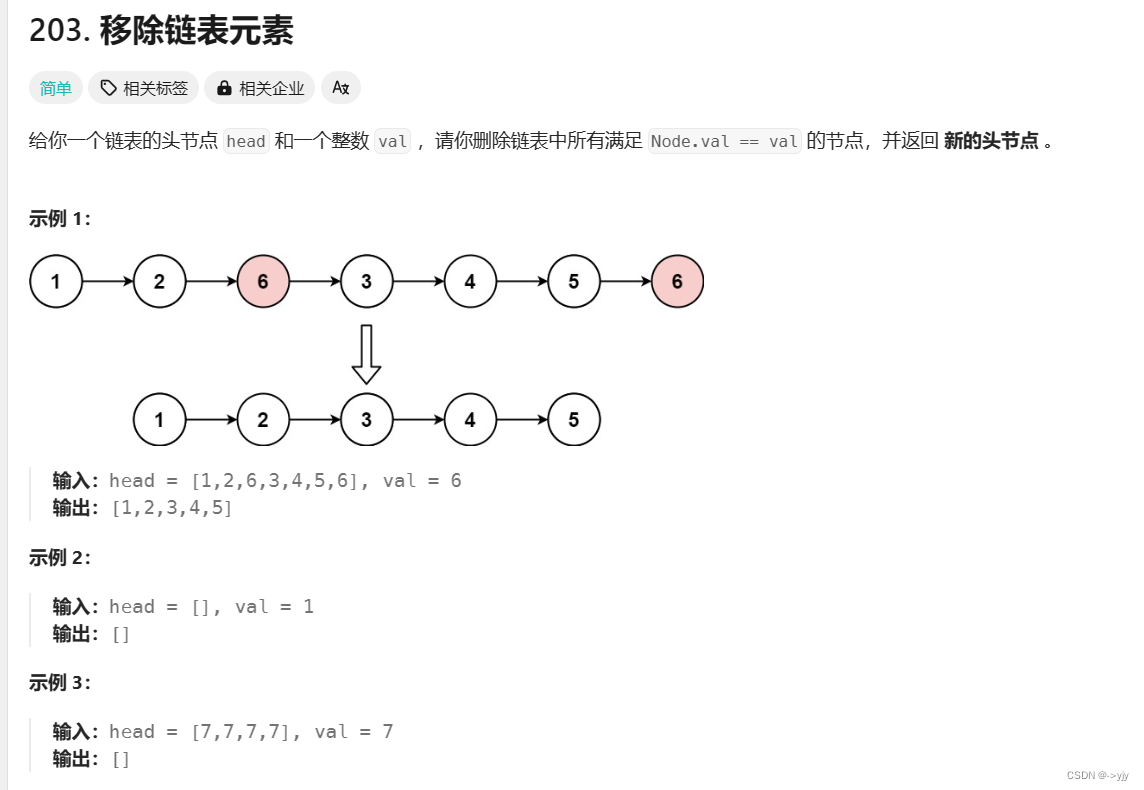
203. 移除链表元素 - 力扣(LeetCode)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* removeElements(struct ListNode* head, int val) {
struct ListNode* cur = head;
struct ListNode*prev = NULL;
while(cur){
if(cur->val == val){
if(cur==head){//头删
cur=head->next;
free(head);
head= cur;
}else{
prev->next = cur->next;
free(cur);
cur = prev->next;
}
}
else{
//找到val值对应的地址(遍历链表)
prev = cur;
cur=cur->next;
}
}
return head;
}206. 反转链表 - 力扣(LeetCode)
struct ListNode* reverseList(struct ListNode* head) {
//记录前中后三个位置
struct ListNode*prev = NULL;
struct ListNode*cur = head;
while(cur != NULL){
struct Listndoe*nextnode = cur->next;
cur->next = prev;
prev = cur;
cur= nextnode;
}
head = prev;
return head;
}876. 链表的中间结点 - 力扣(LeetCode)

/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* middleNode(struct ListNode* head) {
struct ListNode* cur = head;
struct ListNdoe* mid = NULL;
int count = 0;
while(cur){
cur = cur->next;
count++;
}
int n = (count/2);//n为几就需要头删几个
while(n-->0){
mid = head->next;
free(head);
head = mid;
}
return head;
}19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* removeNthFromEnd(struct ListNode* head, int n) {
struct ListNode*phead = head;//这个变量用于求出链表结点个数
struct ListNode* m = head;
struct ListNode* prev = NULL;
int count = 1,i = 0;
while(phead!=NULL){
phead = phead->next;
count++;
}
while(i++<count-n-1){//找到倒数第n个节点
prev = m;
m = m->next;
}
if(m==head){//头删
head = m->next;
free(m);
m = NULL;
}
else{//中间删除
prev->next = m->next;
free(m);
m=NULL;
}
return head;
}21. 合并两个有序链表 - 力扣(LeetCode)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
//若这个地方不判断list是否为空指针,后面部分对tail解引用会报错为空指针解引用
if(list1==NULL){
return list2;
}
if(list2==NULL){
return list1;
}
struct ListNode*n1 = list1;
struct ListNode*n2 = list2;
struct ListNode*head = NULL;
struct ListNode*tail = NULL;//tail随时跟随新链表变动
while(n1&&n2){
if(n1->val >= n2->val){
if(head==NULL){//head最开始为NULL,要先赋值
head = n2;
tail = n2;
}else{
tail->next = n2;
tail = n2;
//tail不断往前走,这样就可以不用每次都遍历链表找到尾再插入
}
n2 = n2->next;
}else if(n1->val < n2->val){
if(head==NULL){
head = n1;
tail = n1;
}else{
tail->next = n1;
tail = n1;
}
n1 = n1->next;
}
}
if(n2){//当n1或者n2其中一空就会跳出来判断
tail->next = n2;
}else if(n1){
tail->next = n1;
}
return head;
}现在有一链表的头指针ListNode* pHead,给一定值x,编写一段代码将所有小于x的节点都排在其余点之前,且不改变原来的数据顺序,返回重新排列后的链表头指针
面试题 02.04. 分割链表 - 力扣(LeetCode)
创建两个带哨兵的链表 然后一大放比x大的 一个放比x小的
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode partition(ListNode head, int x) {
ListNode smlDummy = new ListNode(0),bigDummy = new ListNode(0);
ListNode sml = smlDummy,big = bigDummy;
while(head!=null){
if(head.val<x){
sml.next = head;
sml = sml.next;
}else{
big.next = head;
big = big.next;
}
head = head.next;
}
sml.next = bigDummy.next;
big.next = null;
return smlDummy.next;
}
}234. 回文链表 - 力扣(LeetCode)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
bool isPalindrome(struct ListNode* head) {
struct ListNode*n = head;
struct ListNode*m = head;
while(m && m->next){//找到中间的节点的新方法,这个地方循环后中间节点为n,可以自己画图验证
n = n->next;
m = m->next->next;
}//n为中间结点
struct ListNode*cur = n;
struct ListNode*prev =NULL;
struct ListNode*next = n->next;
while(cur){//反转链表
cur->next = prev;
prev = cur;
cur = next;
if(next){
next = next->next;
}
}//prev 为反转后的头
struct ListNode*phead = head;
while(phead&&prev){//比较两个链表,当一个链表为NULL的时候就停止
if(phead->val!=prev->val){
return false;
}else{
phead= phead->next;
prev = prev->next;
}
}
return true;
}160. 相交链表 - 力扣(LeetCode)
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode A =headA,B = headB;
while(A!=B){
A = A!=null?A.next:headB;
B =B!=null?B.next:headA;
}
return A;
}
}将两个递增的有序链表合并为一个递增的有序链表.要求结果链表仍使用原来两个链表的存储空间
不另外占用其他的存储空间.表中不允许有重复的数据.
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
/*
思路:La,Lb是工作指针 当La和Lb所指向的元素值不同的时候,较小的值链接到Lc上
La和Lb所指向的元素值相同的时候,将La的值链接到Lc上,Lb上的删掉
*/
#include <iostream>
using namespace std;
// 定义链表结点结构
struct ListNode {
int data;
ListNode *next;
};
// 定义链表头指针类型
typedef ListNode* LinkList;
// 合并两个有序链表
void MergeList(LinkList &La, LinkList &Lb, LinkList &Lc)
{
ListNode *pa = La->next; // La 的工作指针,初始化为第一个结点
ListNode *pb = Lb->next; // Lb 的工作指针,初始化为第一个结点
Lc = La; // 用 La 的头结点作为 Lc 的头结点
ListNode *pc = Lc; // Lc 的工作指针
while (pa && pb) {
if (pa->data < pb->data) {
pc->next = pa; // 将 pa 链接在 pc 的后面
pc = pa; // pc 指针后移
pa = pa->next; // pa 指针后移
} else if (pa->data > pb->data) {
pc->next = pb; // 将 pb 链接在 pc 的后面
pc = pb; // pc 指针后移
pb = pb->next; // pb 指针后移
} else { // 相等时取 La 中的元素,删除 Lb 中的元素
pc->next = pa; // 将 pa 链接在 pc 的后面
pc = pa; // pc 指针后移
pa = pa->next; // pa 指针后移
ListNode *q = pb->next; // 保存 pb 的下一个结点
delete pb; // 删除 pb 结点
pb = q; // pb 指针后移
}
}
// 插入剩余段
pc->next = pa ? pa : pb;
// 释放 Lb 的头结点
delete Lb;
}
int main() {
// 测试代码
// 创建两个链表 La 和 Lb,并初始化它们
LinkList La = new ListNode();
La->next = NULL;
LinkList Lb = new ListNode();
Lb->next = NULL;
// 填充链表 La
ListNode *p = La;
for (int i = 1; i <= 5; i += 2) {
ListNode *node = new ListNode();
node->data = i;
node->next = NULL;
p->next = node;
p = node;
}
// 填充链表 Lb
p = Lb;
for (int i = 2; i <= 6; i += 2) {
ListNode *node = new ListNode();
node->data = i;
node->next = NULL;
p->next = node;
p = node;
}
// 打印合并前的链表
std::cout << "La: ";
for (p = La->next; p != NULL; p = p->next)
std::cout << p->data << " ";
std::cout << "\nLb: ";
for (p = Lb->next; p != NULL; p = p->next)
std::cout << p->data << " ";
std::cout << "\n";
// 合并链表
LinkList Lc;
MergeList(La, Lb, Lc);
// 打印合并后的链表
std::cout << "Lc: ";
for (p = Lc->next; p != NULL; p = p->next)
std::cout << p->data << " ";
std::cout << "\n";
// 释放链表
p = Lc;
while (p != NULL) {
ListNode *q = p->next;
delete p;
p = q;
}
return 0;
}
//3)已知两个链表 A 和 B 分别表示两个集合,其元素递增排列。请设计算法求出 A 与 B
//的交集,并存放于 A 链表中。
//[题目分析]
//只有同时出现在两集合中的元素才出现在结果表中, 合并后的新表使用头指针 Lc 指向。
//pa 和 pb 分别是链表 La 和 Lb 的工作指针, 初始化为相应链表的第一个结点, 从第一个结点开
//始进行比较,当两个链表 La 和 Lb 均为到达表尾结点时,如果两个表中相等的元素时,摘取
//La 表中的元素,删除 Lb 表中的元素;如果其中一个表中的元素较小时,删除此表中较小的
//元素,此表的工作指针后移。当链表 La 和 Lb 有一个到达表尾结点,为空时,依次删除另一
//个非空表中的所有元素。
//
#include <iostream>
struct Node {
int data; // 数据
Node* next; // 指向下一个节点的指针
// 构造函数
Node(int val) : data(val), next(nullptr) {}
};
typedef Node* LinkList; // 定义链表类型
void Mix(LinkList& La, LinkList& Lb, LinkList& Lc) {
Node* pa = La->next; // 指向链表 La 的当前节点
Node* pb = Lb->next; // 指向链表 Lb 的当前节点
Node* pc = La; // Lc 的工作指针,初始化为 La 的头结点
Node* u; // 用于暂存要删除的节点
Lc = La;
while (pa && pb) {
if (pa->data == pb->data) { // 如果两个节点数据相等(交集部分)
pc->next = pa; // 将当前节点接入结果链表
pc = pa; // pc 指向新接入的节点
pa = pa->next; // pa 向后移动
u = pb; // 暂存要删除的节点 pb
pb = pb->next; // pb 向后移动
delete u; // 删除节点 pb
}
else if (pa->data < pb->data) {
u = pa; // 暂存要删除的节点 pa
pa = pa->next; // pa 向后移动
delete u; // 删除节点 pa
}
else {
u = pb; // 暂存要删除的节点 pb
pb = pb->next; // pb 向后移动
delete u; // 删除节点 pb
}
}
// 处理剩余的节点
while (pa) {
u = pa; // 暂存要删除的节点 pa
pa = pa->next; // pa 向后移动
delete u; // 删除节点 pa
}
while (pb) {
u = pb; // 暂存要删除的节点 pb
pb = pb->next; // pb 向后移动
delete u; // 删除节点 pb
}
pc->next = NULL; // 置链表尾标记
delete Lb; // 释放 Lb 的头结点
}
( 4)已知两个链表 A 和 B 分别表示两个集合,其元素递增排列。请设计算法求出两个集
合 A 和 B 的差集(即仅由在 A 中出现而不在 B 中出现的元素所构成的集合) ,并以同样的形
式存储,同时返回该集合的元素个数。
[ 题目分析 ]
求两个集合 A 和 B 的差集是指在 A 中删除 A 和 B 中共有的元素,即删除链表中的相应结
点 , 所以要保存待删除结点的前驱,使用指针 pre 指向前驱结点。 pa 和 pb 分别是链表 La 和
Lb 的工作指针 , 初始化为相应链表的第一个结点,从第一个结点开始进行比较,当两个链表
La 和 Lb 均为到达表尾结点时,如果 La 表中的元素小于 Lb 表中的元素, pre 置为 La 表的工
作指针 pa 删除 Lb 表中的元素;如果其中一个表中的元素较小时,删除此表中较小的元素,
此表的工作指针后移。 当链表 La 和 Lb 有一个为空时, 依次删除另一个非空表中的所有元素.
*
将两个非递减的有序链表合并为一个非递增的有序链表。 要求结果链表仍使用原来
两个链表的存储空间 , 不另外占用其它的存储空间。表中允许有重复的数据。
[ 题目分析 ]
合并后的新表使用头指针 Lc 指向, pa 和 pb 分别是链表 La 和 Lb 的工作指针 , 初始化为
相应链表的第一个结点,从第一个结点开始进行比较,当两个链表 La 和 Lb 均为到达表尾结
点时,依次摘取其中较小者重新链接在 Lc 表的表头结点之后,如果两个表中的元素相等,只
摘取 La 表中的元素,保留 Lb 表中的元素。当一个表到达表尾结点,为空时,将非空表的剩
余元素依次摘取,链接在 Lc 表的表头结点之后。
*/
#include <iostream>
using namespace std;
void Difference(LinkList& La, LinkList& Lb, int *n) {
Node *pa = La->next; // 指向链表 La 的当前节点
Node *pb = Lb->next; // 指向链表 Lb 的当前节点
Node *pre = La; // pre 为 La 中 pa 所指结点的前驱结点的指针
Node *u; // 用于暂存要删除的节点
*n = 0; // 初始化结果集合中元素个数为 0
while (pa && pb) {
if (pa->data < pb->data) {
pre = pa; // A 链表中当前结点指针后移
pa = pa->next;
(*n)++; // 计数器加一,表示找到一个差集元素
} else if (pa->data > pb->data) {
pb = pb->next; // B 链表中当前结点指针后移
} else { // pa->data == pb->data,即 A 和 B 中当前结点数据相同
pre->next = pa->next; // 删除 A 中当前结点
u = pa;
pa = pa->next;
delete u; // 释放结点空间
}
}
// 处理 A 中剩余的节点,这些节点都是 A 中独有的元素
while (pa) {
u = pa; // 暂存要删除的节点 pa
pa = pa->next; // pa 向后移动
delete u; // 删除节点 pa
(*n)++; // 计数器加一,表示找到一个差集元素
}
// 由于 B 中剩余的节点都是不会出现在 A 中的元素,无需处理
pre->next = nullptr; // 置链表尾标记
// 释放 Lb 的头结点
delete Lb;
}
5)设计算法将一个带头结点的单链表 A 分解为两个具有相同结构的链表 B、C,其中 B
表的结点为 A 表中值小于零的结点,而 C 表的结点为 A 表中值大于零的结点(链表 A 中的元素为非零整数,要求 B、 C 表利用 A 表的结点) 。[ 题目分析 ]
B 表的头结点使用原来 A 表的头结点,为 C 表新申请一个头结点。从 A 表的第一个结点
开始,依次取其每个结点 p,判断结点 p 的值是否小于 0,利用前插法,将小于 0 的结点插入B 表 , 大于等于 0 的结点插入 C 表。
#include <stdio.h>
#include <stdlib.h>
// 定义链表结点结构
typedef struct Node {
int data;
struct Node *next;
} Node;
// 创建新结点
Node* createNode(int data) {
Node *newNode = (Node *)malloc(sizeof(Node));
if (!newNode) {
printf("内存分配失败\n");
exit(1);
}
newNode->data = data;
newNode->next = NULL;
return newNode;
}
// 打印链表
void printList(Node *head) {
Node *current = head->next; // 跳过头结点
while (current != NULL) {
printf("%d -> ", current->data);
current = current->next;
}
printf("NULL\n");
}
// 释放链表内存
void freeList(Node *head) {
Node *current = head;
Node *next;
while (current != NULL) {
next = current->next;
free(current);
current = next;
}
}
// 分解链表
void splitList(Node *A, Node *B, Node *C) {
Node *current = A->next; // 跳过头结点
Node *tailB = B; // B 表的尾指针
Node *tailC = C; // C 表的尾指针
while (current != NULL) {
if (current->data < 0) {
tailB->next = current;
tailB = current;
} else if (current->data > 0) {
tailC->next = current;
tailC = current;
}
current = current->next;
}
// 断开 B 和 C 表的最后一个结点
tailB->next = NULL;
tailC->next = NULL;
}
int main() {
// 初始化链表 A
Node *A = createNode(0); // 带头结点
Node *current = A;
int values[] = {3, -1, 5, -2, 8, -6, 7}; // 示例数据
for (int i = 0; i < sizeof(values)/sizeof(values[0]); i++) {
current->next = createNode(values[i]);
current = current->next;
}
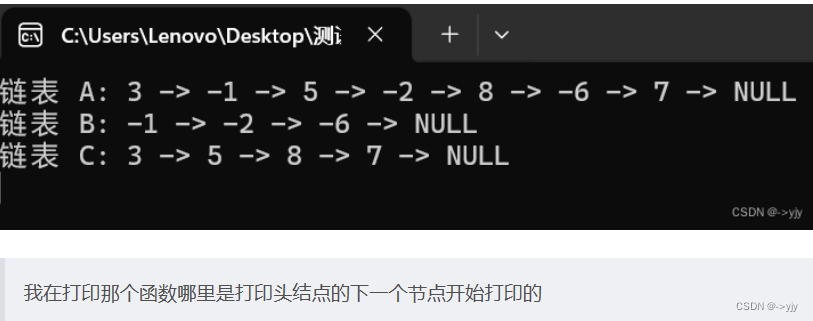
printf("链表 A: ");
printList(A);
// 初始化链表 B 和 C 的头结点
Node *B = createNode(0); // 带头结点
Node *C = createNode(0); // 带头结点
// 分解链表
splitList(A, B, C);
printf("链表 B: ");
printList(B);
printf("链表 C: ");
printList(C);
// 释放链表内存
freeList(A);
freeList(B);
freeList(C);
return 0;
}
( 6)设计一个算法,通过一趟遍历在单链表中确定值最大的结点。
//( 6)设计一个算法,通过一趟遍历在单链表中确定值最大的结点。
#include <iostream>
#include <climits>
struct ListNode {
int value;
ListNode* next;
ListNode(int x) : value(x), next(NULL) {}
};
ListNode* findMaxNode(ListNode* head) {
if (!head) {
return NULL;
}
ListNode* max_value_node = head;
ListNode* current = head->next;
while (current) {
if (current->value > max_value_node->value) {
max_value_node = current;
}
current = current->next;
}
return max_value_node;
}
int main() {
// 创建一个链表用于测试
ListNode* node5 = new ListNode(3);
ListNode* node4 = new ListNode(1);
node4->next = node5;
ListNode* node3 = new ListNode(4);
node3->next = node4;
ListNode* node2 = new ListNode(2);
node2->next = node3;
ListNode* head = new ListNode(5);
head->next = node2;
// 调用函数并输出结果
ListNode* max_node = findMaxNode(head);
if (max_node) {
std::cout << "最大值节点的值是: " << max_node->value << std::endl;
} else {
std::cout << "链表为空" << std::endl;
}
// 释放分配的内存
delete node5;
delete node4;
delete node3;
delete node2;
delete head;
return 0;
}
( 7)设计一个算法,通过遍历一趟,将链表中所有结点的链接方向逆转,仍利用原表的
存储空间。
// 逆转链表
#include<iostream>
using namespace std;
struct ListNode{
int value;
ListNode* next;
ListNode(int x=0):value(x),next(NULL){}
};
ListNode*reverseList(ListNode*head) {
ListNode*prev = NULL;
ListNode* current = head;
while(current){
ListNode*next = current->next;//保存当前节点的下一个节点
current->next = prev;//反转当前节点指针;
prev = current;//更新prev为当前节点
current = next;//移动到下一个节点
}
return prev;//prev现在是新的头结点
}
int main()
{
//创建一个链表用于测试
ListNode*node5 = new ListNode(5);
ListNode*node4 = new ListNode(4);
node4->next = node5;
ListNode*node3 = new ListNode(3);
node3->next = node4;
ListNode* node2 = new ListNode(2);
node2->next = node3;
ListNode*head = new ListNode(1);
head->next = node2;
//打印原链表
cout<<"原链表:";
ListNode*temp = head;
while(temp){
cout<<temp->value<<" ";
temp = temp->next;
}
cout<<endl;
///调用函数反转链表
ListNode*new_head = reverseList(head);
//打印反转后的链表
cout<<"反转后的链表:";
temp = new_head;
while(temp){
cout<<temp->value<<" ";
temp = temp->next;
}
cout<<endl;
//释放分配的内存
delete node5;
delete node4;
delete node3;
delete node2;
delete head;
return 0;
}
( 8)设计一个算法,删除递增有序链表中值大于 mink 且小于 maxk 的所有元素( mink
和 maxk 是给定的两个参数,其值可以和表中的元素相同,也可以不同 )。
#include <iostream>
struct ListNode {
int value;
ListNode* next;
ListNode(int x) : value(x), next(nullptr) {}
};
ListNode* removeElementsInRange(ListNode* head, int mink, int maxk) {
// 创建哨兵节点
ListNode* dummy = new ListNode(0);
dummy->next = head;
ListNode* prev = dummy;
ListNode* current = head;
while (current) {
if (current->value > mink && current->value < maxk) {
prev->next = current->next; // 跳过当前节点
} else {
prev = current; // 继续遍历
}
current = current->next; // 移动到下一个节点
}
// 更新头节点
ListNode* new_head = dummy->next;
delete dummy; // 释放哨兵节点的内存
return new_head;
}
int main() {
// 创建一个递增有序链表用于测试
ListNode* node5 = new ListNode(6);
ListNode* node4 = new ListNode(5);
node4->next = node5;
ListNode* node3 = new ListNode(4);
node3->next = node4;
ListNode* node2 = new ListNode(3);
node2->next = node3;
ListNode* head = new ListNode(1);
head->next = node2;
int mink = 2;
int maxk = 5;
// 打印原链表
std::cout << "原链表: ";
ListNode* temp = head;
while (temp) {
std::cout << temp->value << " ";
temp = temp->next;
}
std::cout << std::endl;
// 调用函数删除指定范围的元素
ListNode* new_head = removeElementsInRange(head, mink, maxk);
// 打印删除后的链表
std::cout << "删除后的链表: ";
temp = new_head;
while (temp) {
std::cout << temp->value << " ";
temp = temp->next;
}
std::cout << std::endl;
// 释放分配的内存
delete node5;
delete node4;
delete node3;
delete node2;
delete head;
return 0;
}
( 9)已知 p 指向双向循环链表中的一个结点, 其结点结构为 data 、prior 、next 三个域,
写出算法 change, 交换 p 所指向的结点和它的前缀结点的顺序。
#include <iostream>
struct ListNode {
int data;
ListNode* prior;
ListNode* next;
ListNode(int x) : data(x), prior(nullptr), next(nullptr) {}
};
void change(ListNode* p) {
if (p == nullptr || p->prior == nullptr) {
return; // 无法交换
}
ListNode* Q = p->prior; // Q 是 p 的前驱节点
ListNode* Q_prior = Q->prior; // Q 的前驱节点
ListNode* P_next = p->next; // P 的后继节点
// 交换 P 和 Q 的指针
if (Q_prior != nullptr) {
Q_prior->next = p;
}
if (P_next != nullptr) {
P_next->prior = Q;
}
p->prior = Q_prior;
p->next = Q;
Q->prior = p;
Q->next = P_next;
}
void printList(ListNode* head) {
ListNode* temp = head;
do {
std::cout << temp->data << " ";
temp = temp->next;
} while (temp != head);
std::cout << std::endl;
}
int main() {
// 创建一个双向循环链表用于测试
ListNode* node1 = new ListNode(1);
ListNode* node2 = new ListNode(2);
ListNode* node3 = new ListNode(3);
ListNode* node4 = new ListNode(4);
node1->next = node2; node1->prior = node4;
node2->next = node3; node2->prior = node1;
node3->next = node4; node3->prior = node2;
node4->next = node1; node4->prior = node3;
ListNode* head = node1;
// 打印原链表
std::cout << "原链表: ";
printList(head);
// 调用函数交换 node3 和 node2
change(node3);
// 打印交换后的链表
std::cout << "交换后的链表: ";
printList(head);
// 释放分配的内存
delete node1;
delete node2;
delete node3;
delete node4;
return 0;
}
( 10)已知长度为 n 的线性表 A 采用顺序存储结构,请写一时间复杂度为 O(n) 、空间复
杂度为 O(1) 的算法,该算法删除线性表中所有值为 item 的数据元素。
#include <iostream>
void removeItem(int* A, int& n, int item) {
int j = 0; // j 指向下一个保留的位置
for (int i = 0; i < n; ++i) {
if (A[i] != item) {
A[j] = A[i];
++j;
}
}
// 更新数组长度
n = j;
}
int main() {
// 测试数据
int A[] = {1, 2, 3, 2, 4, 2, 5};
int n = sizeof(A) / sizeof(A[0]);
int item = 2;
std::cout << "原数组: ";
for (int i = 0; i < n; ++i) {
std::cout << A[i] << " ";
}
std::cout << std::endl;
// 删除所有值为 item 的元素
removeItem(A, n, item);
std::cout << "删除后的数组: ";
for (int i = 0; i < n; ++i) {
std::cout << A[i] << " ";
}
std::cout << std::endl;
return 0;
}








![[SAP ABAP] 数据类型](https://img-blog.csdnimg.cn/direct/eb21ebc108ec4c82b370150f64ece423.png)