1.接雨水

代码随想录

代码：(单调栈)

class Solution {
public:
    int trap(vector<int>& height) {
        int result = 0;
        stack<int> st;
        st.push(0);
        for(int i = 1; i < height.size(); i++){
            if(height[i] < height[st.top()]){
                st.push(i);
            }else if(height[i] == height[st.top()]){
                st.pop(); // 元素值相等留一个就好了，避免重复计算。不过这句话删了也可以
                st.push(i);
            }else{
                while(!st.empty() && height[i] > height[st.top()]){
                    int mid = st.top();
                    st.pop(); // 这里有了pop操作就要注意让栈不为空时再操作
                    if(!st.empty()){
                        int h = min(height[i],height[st.top()]) - height[mid];
                        int w = i - st.top() - 1;
                        result += h * w;
                    }
                }
                st.push(i);
            }
        }
        return result;
    }
};

思路：（这里是横着求矩形面积的）

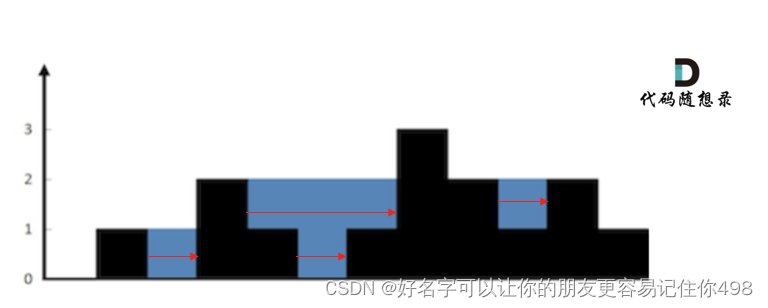
其实就是找每个元素前面第一个比它大的值（就是单调栈里的栈顶元素的下一个值），和后面第一个比它大的值（用单调栈，第一次比栈顶元素大的当前遍历的元素值）。

矩形的高=这两个值高度的最小值-当前计算的元素高度

矩形的宽=后面元素下标值-前面元素的下标值-1

注意：单调栈里存的都是下标。

2.柱状图中最大的矩形

 代码随想录

代码： （单调栈）

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int result = 0;
        stack<int> st;
        heights.insert(heights.begin(),0);
        heights.push_back(0);
        // 向数组首位位置加0，为了避免 因为数组本身就单调 而出现 没有走到计算面积的步骤
        st.push(0);
        for(int i = 1; i < heights.size(); i++){
            if(heights[i] > heights[st.top()]){
                st.push(i);
            }else if(heights[i] == heights[st.top()]){
                st.pop();
                st.push(i);
            }else{
                while(!st.empty() && heights[i] < heights[st.top()]){
                    int h = heights[st.top()];
                    st.pop();
                    if(!st.empty()){
                        int w = i - st.top() - 1;
                        int sum = w * h;
                        result = max(result,sum);
                    }
                }
                st.push(i);
            }
        }
        return result;
    }
};

思路：

和接雨水的区别就是，这里用的是递减栈，以及需要在数组首末补0

基于每一个高度，求左右两边最邻近的比它高度小的元素。

矩形的高=当前计算的元素高度

矩形的宽=后面元素下标值-前面元素的下标值-1

首先来说末尾为什么要加元素0？

如果数组本身就是升序的，例如[2,4,6,8]，那么入栈之后 都是单调递减，一直都没有走 情况三 计算结果的哪一步，所以最后输出的就是0了。

开头为什么要加元素0？

如果数组本身是降序的，例如 [8,6,4,2]，在 8 入栈后，6 开始与8 进行比较，此时我们得到 mid（8），rigt（6），但是得不到 left。

（mid、left，right 都是对应版本一里的逻辑）

因为 将 8 弹出之后，栈里没有元素了，那么为了避免空栈取值，直接跳过了计算结果的逻辑。

之后又将6 加入栈（此时8已经弹出了），然后 就是 4 与 栈口元素 8 进行比较，周而复始，那么计算的最后结果resutl就是0