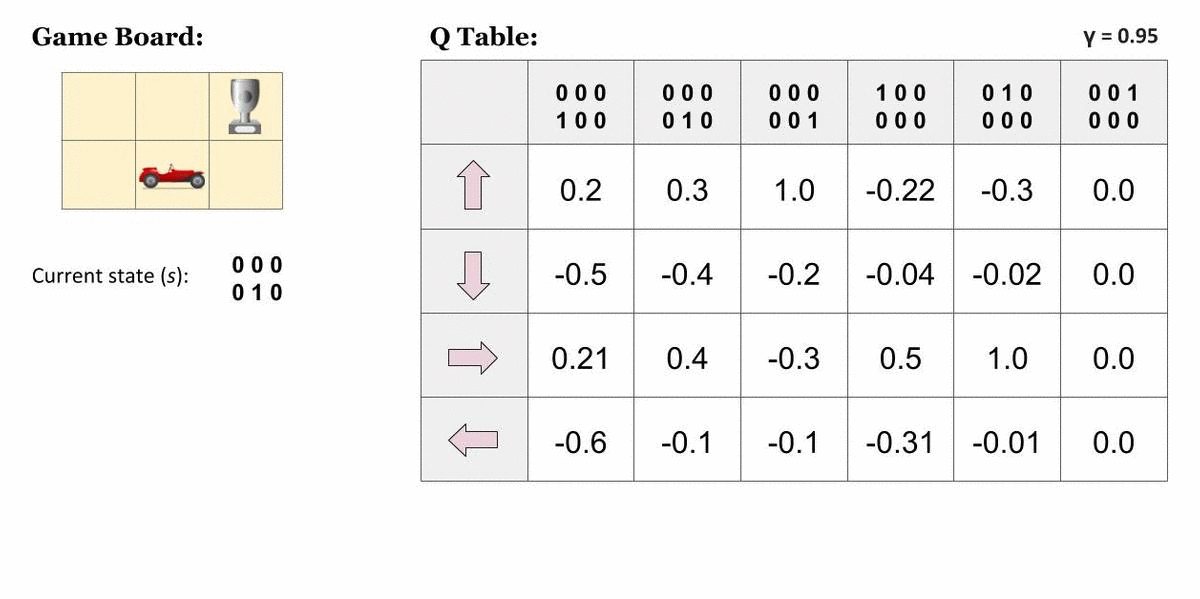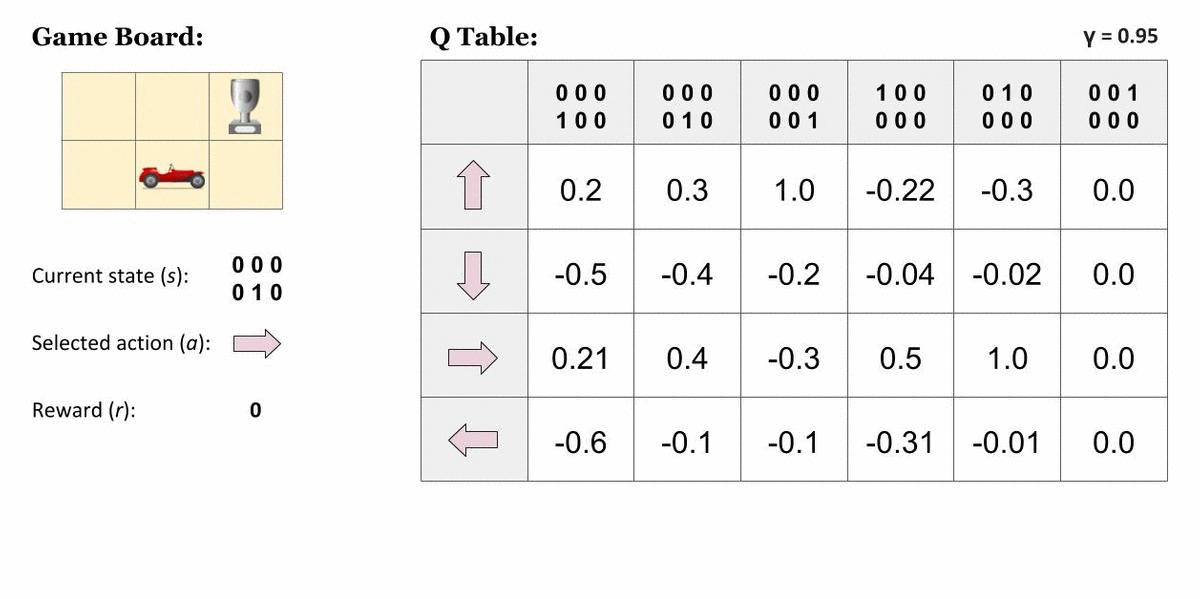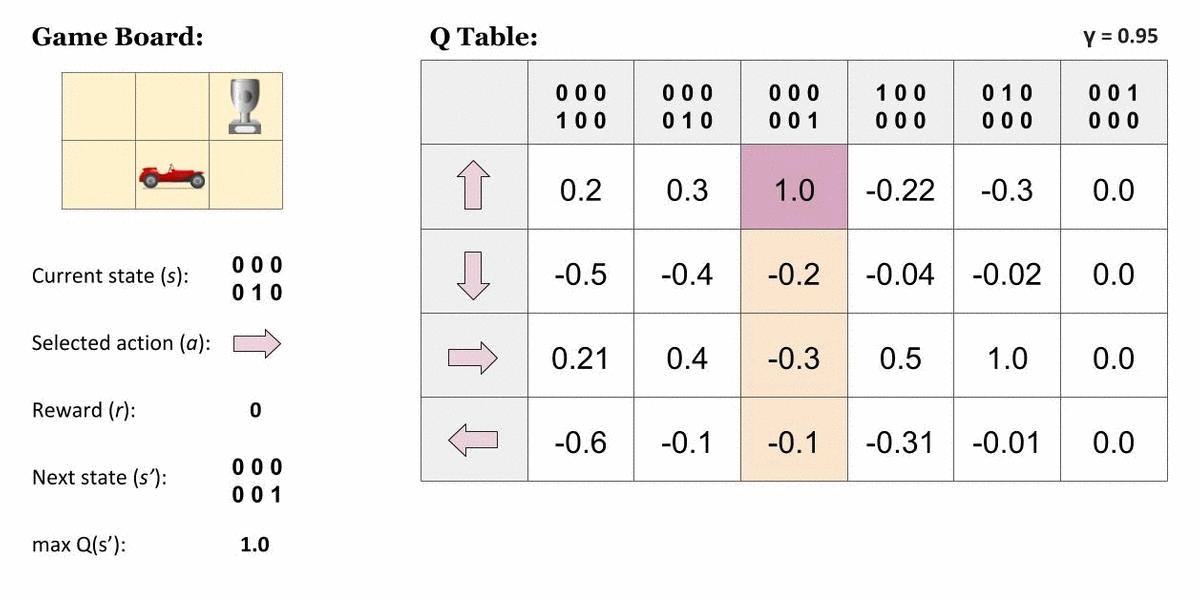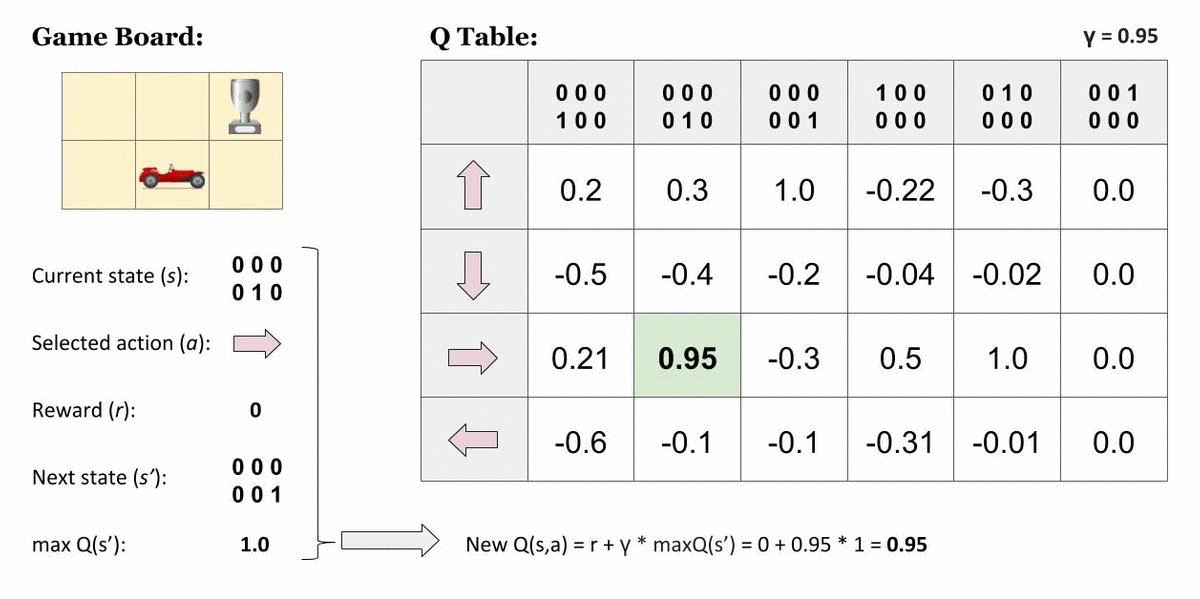
先这样吧，，专业课不是统考，我发现每年的卷子风格都不太一样，侧重点也不一样。以及21的和16的发生了很大的改变。等明年1月再看看吧

那就先over啦

数据结构撒花！！！！！！！！！

等我7.4开电子技术基础！！！ 

---

---

---

下面程序的时间复杂为
for（i=1，s=0； i<=n； i++） {       n
t=1；
for(j=1；j<=i；j++)        S = n*(n+1)/2
t=t*j；                    S = n*(n+1)/2
s=s+t；                    n      }

该程序的时间复杂度分析如下：

外层循环是以 `i` 为变量，从 1 遍历到 `n`，因此外层循环执行了 `n` 次。

内层循环是以 `j` 为变量，每次外层循环中，`j` 会从 1 遍历到当前 `i` 的值。这意味着：

- 当 `i=1` 时，内层循环执行 1 次，
- 当 `i=2` 时，内层循环执行 2 次，
- ...
- 当 `i=n` 时，内层循环执行 `n` 次。

因此，内层循环总共执行的次数是 `1 + 2 + 3 + ... + n`，这是一个等差数列求和的问题，其和可以用公式计算：`S = n*(n+1)/2`。

内层循环中的操作 `t=t*j` 是常数时间操作，但需要执行 `S = n*(n+1)/2` 次，

而外层循环中的 `s=s+t` 同样是常数时间操作，执行了 `n` 次。

因此，整体的时间复杂度由最内层循环主导，即 `O(n*(n+1)/2)`。在大O表示法中，可以忽略低阶项和系数，所以最终的时间复杂度为 `O(n^2)`。

---

---

---

数据结构合集 - 二叉搜索树(二叉排序树)(二叉查找树)_哔哩哔哩_bilibili 

二叉搜索树(二叉排序树)(二叉查找树)（BST）

所有的父节点来说，它的左孩子一定小于右孩子

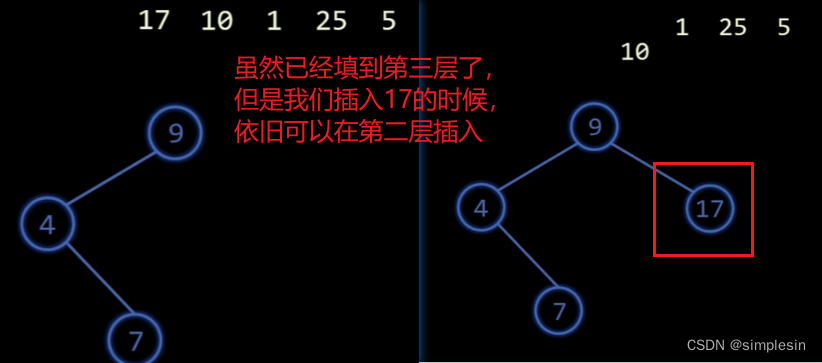
极端情况，采用平衡二叉树的调整 的方法

数据结构笔记20-37-CSDN博客

 

---

---

---

 

---

---

---

 

---

---

---

 

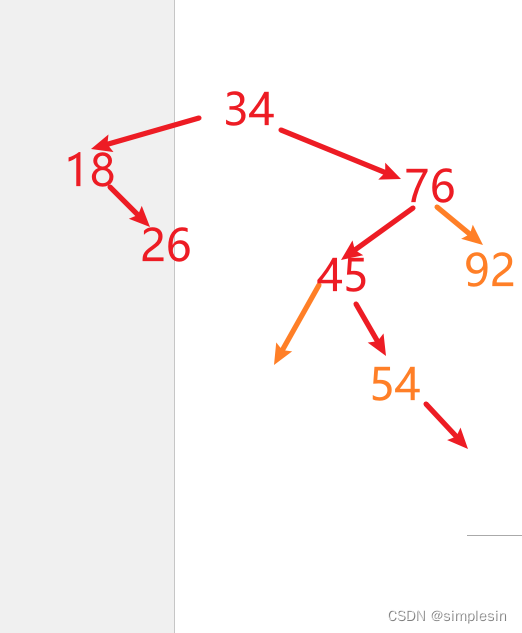
实际上，(A) 快速排序、(B) 堆排序、(C) 归并排序 的时间复杂度在最坏情况和平均情况下是不同的：

• 快速排序：它的平均时间复杂度是O(n log n)，这是非常优秀的。但在最坏情况下（例如已经排序好的数组），时间复杂度会退化到O(n^2)。快速排序不需要额外的存储空间（如果采用原地排序的话），但其性能依赖于pivot的选择。

• 堆排序：堆排序的时间复杂度在最好、最坏和平均情况下均为O(n log n)。它首先通过构建一个最大堆或最小堆（本题中为找最小元素，故构建最小堆），然后不断移除堆顶元素并重新调整堆，直到找到所需的最小元素。堆排序需要一个额外的O(1)空间复杂度用于交换元素，但主要操作还是在原数组上进行。

• 归并排序：归并排序的时间复杂度在所有情况下都是O(n log n)，是非常稳定的排序算法。但它需要O(n)的额外空间来合并子数组，这使得它在空间效率上不如堆排序和快速排序（如果不考虑快速排序的最坏情况）。

对于题目要求的“选出其中最小的10个记录关键字”，堆排序（B）的优势在于它可以直接通过调整堆来高效地获取顶部的元素，而不需要完全排序整个数组。相比快速排序和归并排序，堆排序在这个特定任务上的效率更高，因为它天然支持快速访问顶部元素（即最小元素），并且不需要像快速排序那样担心最坏情况性能退化，也不像归并排序那样需要大量额外空间。因此，选项B是最合适的选择。

---

---

---