在现代科技的引领下,艺术与VR虚拟现实技术相融合必将成为趋势,深圳VR公司华锐视点荣幸地推出VR艺术品虚拟展厅,为您带来前所未有的艺术观赏体验。体验者足不出户即可置身于一个充满创意与灵感的虚拟艺术空间。
我们深入了解每一位客户的需求与期望,从展览的主题、内容到细节,都经过精心策划与设计。借助先进的web3D开发建模技术,将展览空间和展品进行精细的虚拟建模。再通过专业的渲染技术,为虚拟展厅添加逼真的材质和光照效果,让您仿佛置身于真实的艺术殿堂之中。
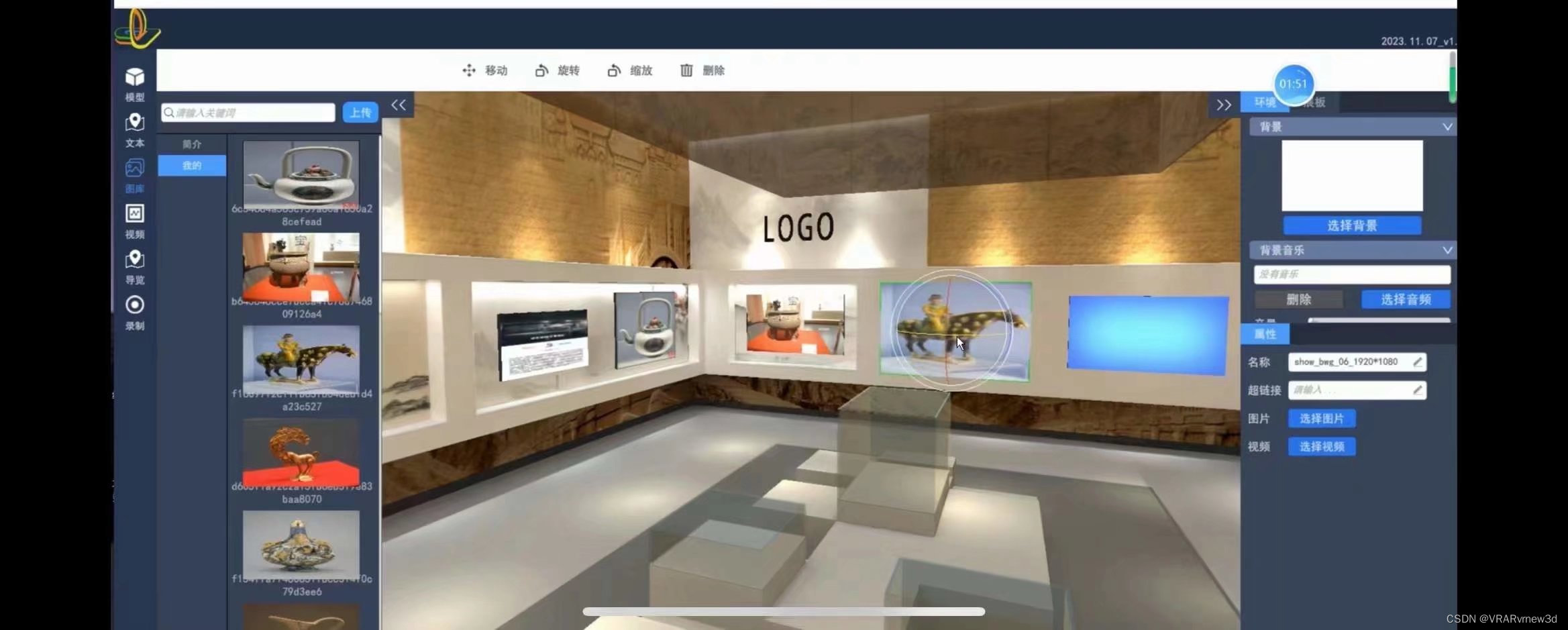
为了让您的展览更加生动有趣,我们特别设计了丰富的动画效果和互动环节。观众通过3D动画效果深入了解展品的细节与特点,同时,与虚拟展厅的互动功能将为他们带来全新的观赏体验。
对于学生而言,VR艺术品虚拟展厅是一个宝贵的资源。他们可以通过这个平台深入了解不同时期、不同风格的艺术作品,培养审美情趣和艺术鉴赏能力。同时,这个虚拟空间也将激发他们对艺术的热爱和创造力的发展。体验3D内容,教学3D知识,上华锐云空间。互动性强,更直观,更吸引人!https://www.ykjhr.com/
对于商业领域而言,VR艺术品虚拟展厅成为了一种独特的品牌推广工具。它不仅能够展示企业的文化理念和品牌形象,还能够为公众提供线上文化服务,确保教育活动的连续性和广泛性。







![[WTL/Win32]_[中级]_[MVP架构在实际项目中的应用]](https://img-blog.csdnimg.cn/direct/466ffe7b1bcf4f74a032871c30ad58b8.png)



