目录

一、问题描述

二、解题思路

三、代码实现

四、刷题链接

---

一、问题描述

二、解题思路

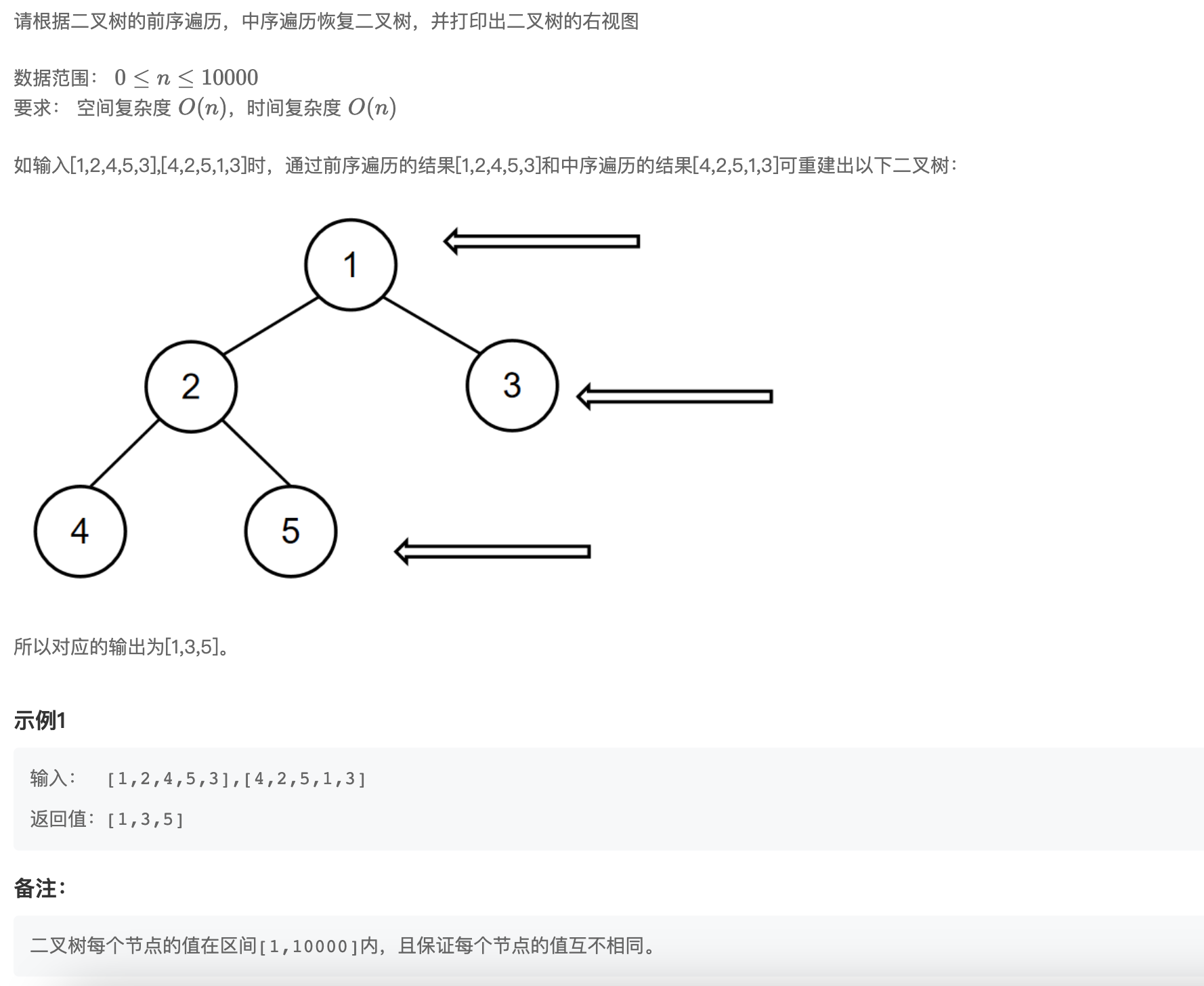
这里右视图类似于立方体的右视图，从右边看每一层第一个看到的结点的集合就是需要返回的结果，注意返回的结点是有相对顺序的，比如上面的1,3,5对应第一层、第二层、第三层结点；返回1,5,3是不对的。

1.这里使用比较直接的方法，先使用先序遍历和中序遍历序列构造二叉树

2.然后对这个二叉树进行层序遍历，对每一层的最后一个结点（每一层的右视图）统计，最后返回

三、代码实现

import java.util.*;

class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;
    public TreeNode(int val) {
      this.val = val;
    }
}

public class Solution {
    ArrayList<Integer> resArr=new ArrayList<>();
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 求二叉树的右视图
     * @param preOrder int整型一维数组 先序遍历
     * @param inOrder int整型一维数组 中序遍历
     * @return int整型一维数组
     */
    public int[] solve (int[] preOrder, int[] inOrder) {
        //判断是否有值
        if(preOrder.length==0){
            return new int[0];
        }
        TreeNode root=new TreeNode(-1);
        //首先递归构造二叉树
        findMidIdx(root,preOrder,0,preOrder.length-1,inOrder,0,inOrder.length-1);
        //然后对二叉树进行层序遍历，得到每一层的最后一个结点值
        bfs(root);
        int[] resInts=new int[resArr.size()];
        for(int i=0;i<resArr.size();i++){
            resInts[i]=resArr.get(i);
        }
        return resInts;
    }
    public void findMidIdx(TreeNode root,int[] preOrder,int pstart,int pend, int[] inOrder,int istart,int iend){
        int rootval=preOrder[pstart];
        root.val=rootval;
        if(pstart==pend){
            return;
        }
        int midtargetIndex=0;
        for(int i=istart;i<=iend;i++){
            if(inOrder[i]==rootval){
                midtargetIndex=i;
                break;
            }
        }
        int leftsize=midtargetIndex-istart;
        int rightsize=iend-midtargetIndex;
        if(leftsize==0){//剩余全是右子树
            TreeNode rightnode=new TreeNode(-1);
            root.right=rightnode;
            findMidIdx(root.right,preOrder,pstart+1,pend,inOrder,istart+1,iend);
        }else if(midtargetIndex==iend){//剩余全是左子树
            TreeNode leftnode=new TreeNode(-1);
            root.left=leftnode;
            findMidIdx(leftnode,preOrder,pstart+1,pend,inOrder,istart,iend-1);
        }else{
            //对左子树部分
            TreeNode leftnode=new TreeNode(-1);
            root.left=leftnode;
            findMidIdx(leftnode,preOrder,pstart+1,pstart+leftsize,inOrder,istart,midtargetIndex-1);
            //对右子树部分
            TreeNode rightnode=new TreeNode(-1);
            root.right=rightnode;
            findMidIdx(rightnode,preOrder,pend-rightsize+1,pend,inOrder,midtargetIndex+1,iend);
        }
    }
    //使用队列实现层序遍历
    public void bfs(TreeNode root){
        Deque<TreeNode> nodeque=new LinkedList<>();
        nodeque.offer(root);
        int lastlayernodenum=1;
        int nowlayernode=0;
        while(!nodeque.isEmpty()){
            TreeNode nownode=nodeque.poll();
            lastlayernodenum--;
            if(nownode.left!=null){
                nodeque.offer(nownode.left);
                nowlayernode++;
            }
            if(nownode.right!=null){
                nodeque.offer(nownode.right);
                nowlayernode++;
            }
            if(lastlayernodenum==0){
                resArr.add(nownode.val);
                lastlayernodenum=nowlayernode;
                nowlayernode=0;
            }
        }
    }
}

四、刷题链接

输出二叉树的右视图_牛客题霸_牛客网