XGBoost算法详解

XGBoost（Extreme Gradient Boosting）是一种高效的梯度提升决策树（GBDT）实现，因其高性能和灵活性在机器学习竞赛中广泛使用。本文将详细介绍XGBoost算法的原理，并展示其在实际数据集上的应用。

XGBoost算法原理

XGBoost是一种集成学习方法，通过逐步建立多个决策树，每棵树都在前一棵树的基础上进行改进。XGBoost的基本思想是逐步减少损失函数值，使模型的预测能力不断提高。

算法步骤

1. 初始化模型：使用常数模型初始化，比如回归问题中可以用目标值的均值初始化模型。
2. 计算残差：计算当前模型的残差，即预测值与真实值之间的差异。
3. 拟合残差：用新的决策树拟合残差，并更新模型。
4. 更新模型：将新决策树的预测结果加到模型中，以减少残差。
5. 重复步骤2-4：直到达到预设的迭代次数或损失函数值足够小。

公式推理

初始化模型：
$F_0(x)=\arg {\min }_{\gamma }{\sum }_{i=1}^{n}L(y_i,\gamma )$

对于每一次迭代 $m=1,2,\dots ,M$：

1. 计算负梯度（残差）： $r_{im}=-{\left[\frac{\partial L(y_i,F(x_i))}{\partial F(x_i)}\right]}_{F(x)=F_{m-1}(x)}$
2. 拟合一个新的决策树来预测残差：$h_m(x)=\arg {\min }_h{\sum }_{i=1}^n(r_{im}-h(x_i){)}^2$
3. 更新模型：$F_m(x)=F_{m-1}(x)+\nu h_m(x)$
   其中，$\nu$是学习率，控制每棵树对最终模型的贡献。

损失函数与正则化

XGBoost的损失函数包含两部分：训练误差和正则化项。训练误差衡量模型预测值与真实值之间的差距，正则化项则用于控制模型复杂度，以避免过拟合。

损失函数形式如下：
$$\mathcal{L}(F)=\sum _{i=1}^{n}L(y_i,F(x_i))+\sum _{k=1}^K\Omega (f_k)$$
其中，$\Omega (f_k)$是第k棵树的正则化项，通常包括叶子节点数和叶子节点权重的平方和：
$$\Omega (f)=\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$

树结构的构建

XGBoost采用启发式算法来构建树结构。在每个节点分裂时，选择能最大程度上减少损失函数的特征和分割点。具体过程如下：

1. 计算增益：对于每个特征，计算在不同分割点上的增益，增益表示分裂前后损失函数的变化。
2. 选择分割点：选择增益最大的特征和分割点进行节点分裂。
3. 递归构建树：对分裂后的每个子节点重复上述过程，直到达到预设的树深度或其他停止条件。

并行和分布式计算

XGBoost通过并行和分布式计算大大提高了训练速度。其核心思想是将特征按列存储，允许在计算增益时并行处理不同特征。此外，XGBoost还支持分布式计算，能够在多台机器上分布式训练模型。

缺失值处理

XGBoost在训练过程中能够自动处理缺失值。在分裂节点时，针对缺失值分别计算增益，选择最佳策略。通常采用两种方法处理缺失值：默认方向法和分布估计法。

学习率与子采样

XGBoost通过学习率和子采样来控制每棵树对最终模型的贡献。学习率$\nu$用于缩小每棵树的预测值，防止模型过拟合。子采样则通过随机选择训练样本和特征，进一步提高模型的泛化能力。

XGBoost算法的特点

1. 高效性：XGBoost通过并行处理和分布式计算大大提高了训练速度。
2. 灵活性：XGBoost可以处理回归、分类和排序任务，并且可以使用各种损失函数。
3. 鲁棒性：XGBoost对数据的噪声和异常值有一定的鲁棒性。
4. 可解释性：通过特征重要性等方法可以解释XGBoost模型。

XGBoost参数说明

以下是XGBoost常用参数及其详细说明的表格形式：

参数名称	描述	默认值	示例
n_estimators	树的棵数，提升迭代的次数	100	n_estimators=200
learning_rate	学习率，控制每棵树对最终模型的贡献	0.1	learning_rate=0.05
max_depth	树的最大深度，控制每棵树的复杂度	6	max_depth=4
min_child_weight	叶子节点最小权重，控制过拟合	1	min_child_weight=3
subsample	样本采样比例，用于控制过拟合	1.0	subsample=0.8
colsample_bytree	每棵树的特征采样比例	1.0	colsample_bytree=0.8
gamma	节点分裂所需的最小损失函数下降值	0	gamma=0.1
lambda	L2正则化项系数	1	lambda=2
alpha	L1正则化项系数	0	alpha=0.1
scale_pos_weight	正样本的权重比例，用于处理类别不平衡	1	scale_pos_weight=10
objective	要优化的目标函数	reg:squarederror	objective='binary:logistic'
eval_metric	评估指标	rmse	eval_metric='auc'
seed	随机数种子，用于结果复现	0	seed=42
silent	是否静默模式，0表示打印运行信息，1表示不打印	1	silent=0
nthread	线程数，控制并行计算	所有可用线程	nthread=4
max_delta_step	每棵树权重估计的最大步长，如果类别极度不平衡，可以设置较高的值	0	max_delta_step=1
booster	要使用的提升类型，可以是gbtree、gblinear或dart	gbtree	booster='dart'
tree_method	构建树的方法，可以是auto、exact、approx、hist、gpu_hist	auto	tree_method='hist'
predictor	用于预测的算法类型，可以是cpu_predictor或gpu_predictor	auto	predictor='gpu_predictor'

通过合理调整这些参数，可以优化XGBoost模型在特定任务和数据集上的性能。

XGBoost算法在回归问题中的应用

在本节中，我们将使用合成数据集来展示如何使用XGBoost算法进行回归任务。

导入库

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import xgboost as xgb
from sklearn.metrics import mean_squared_error, r2_score

生成和预处理数据

使用 make_regression 函数生成一个合成的回归数据集：

# 生成合成回归数据集
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=42)

# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

训练XGBoost模型

# 训练XGBoost模型
xgb_regressor = xgb.XGBRegressor(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42)
xgb_regressor.fit(X_train, y_train)

预测与评估

# 预测
y_pred = xgb_regressor.predict(X_test)

# 评估
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f'Mean Squared Error: {mse:.2f}')
print(f'R^2 Score: {r2:.2f}')

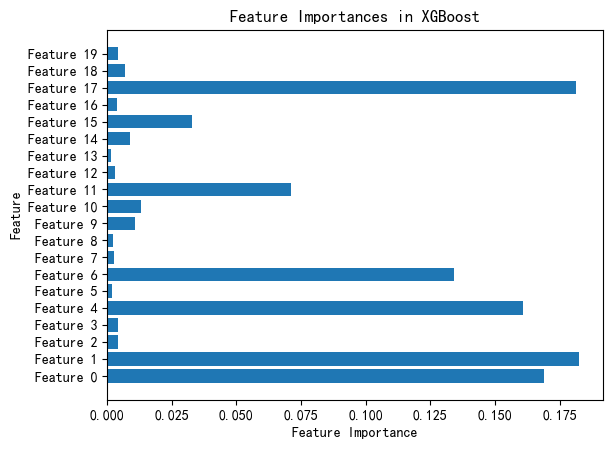
特征重要性

# 特征重要性
feature_importances = xgb_regressor.feature_importances_
plt.barh(range(X.shape[1]), feature_importances, align='center')
plt.yticks(np.arange(X.shape[1]), [f'Feature {i}' for i in range(X.shape[1])])
plt.xlabel('Feature Importance')
plt.ylabel('Feature')
plt.title('Feature Importances in XGBoost')
plt.show()

XGBoost算法在分类问题中的应用

在本节中，我们将使用 make_classification 函数生成一个合成的分类数据集，来展示如何使用XGBoost算法进行分类任务。

导入库

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

生成和预处理数据

# 生成合成分类数据集
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=42)

# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

训练XGBoost模型

# 训练XGBoost模型
xgb_classifier = xgb.XGBClassifier(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42)
xgb_classifier.fit(X_train, y_train)

预测与评估

# 预测
y_pred = xgb_classifier.predict(X_test)

# 评估
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')

# 混淆矩阵
conf_matrix = confusion_matrix(y_test, y_pred)
print('Confusion Matrix:')
print(conf_matrix)

# 分类报告
class_report = classification_report(y_test, y_pred)
print('Classification Report:')
print(class_report)

结语

本文我们详细介绍了XGBoost算法的原理和特点，并展示了其在回归和分类任务中的应用。首先介绍了XGBoost算法的基本思想和公式，然后展示了如何在合成数据集上使用XGBoost进行回归任务，以及如何在合成分类数据集上使用XGBoost进行分类任务。