数据分析第三讲：numpy的应用入门（二）

news2025/2/26 4:39:36

NumPy的应用（二）

数组对象的方法

获取描述统计信息

描述统计信息主要包括数据的集中趋势、离散程度和频数分析等，其中集中趋势主要看均值和中位数，离散程度可以看极值、方差、标准差等，详细的内容大家可以阅读《统计思维系列课程01：解读数据》。

array1 = np.random.randint(1, 100, 10)
array1

输出：

array([46, 51, 15, 42, 53, 71, 20, 62,  6, 94])

计算总和、均值和中位数。

代码：

print(array1.sum())
print(np.sum(array1))
print(array1.mean())
print(np.mean(array1))
print(np.median(array1))
print(np.quantile(array1, 0.5))

说明：上面代码中的mean、median和quantile分别是 NumPy 中计算算术平均值、中位数和分位数的函数，其中quantitle函数的第二个参数设置为0.5表示计算50%分位数，也就是中位数。

输出：

极值、全距和四分位距离。

代码：

print(array1.max())
print(np.amax(array1))
print(array1.min())
print(np.amin(array1))
print(array1.ptp())
print(np.ptp(array1))
q1, q3 = np.quantile(array1, [0.25, 0.75])
print(q3 - q1)

输出：

方差、标准差和变异系数。

代码：

print(array1.var())
print(np.var(array1))
print(array1.std())
print(np.std(array1))
print(array1.std() / array1.mean())

输出：

651.2
651.2
25.51862065237853
25.51862065237853
0.5547526228777941

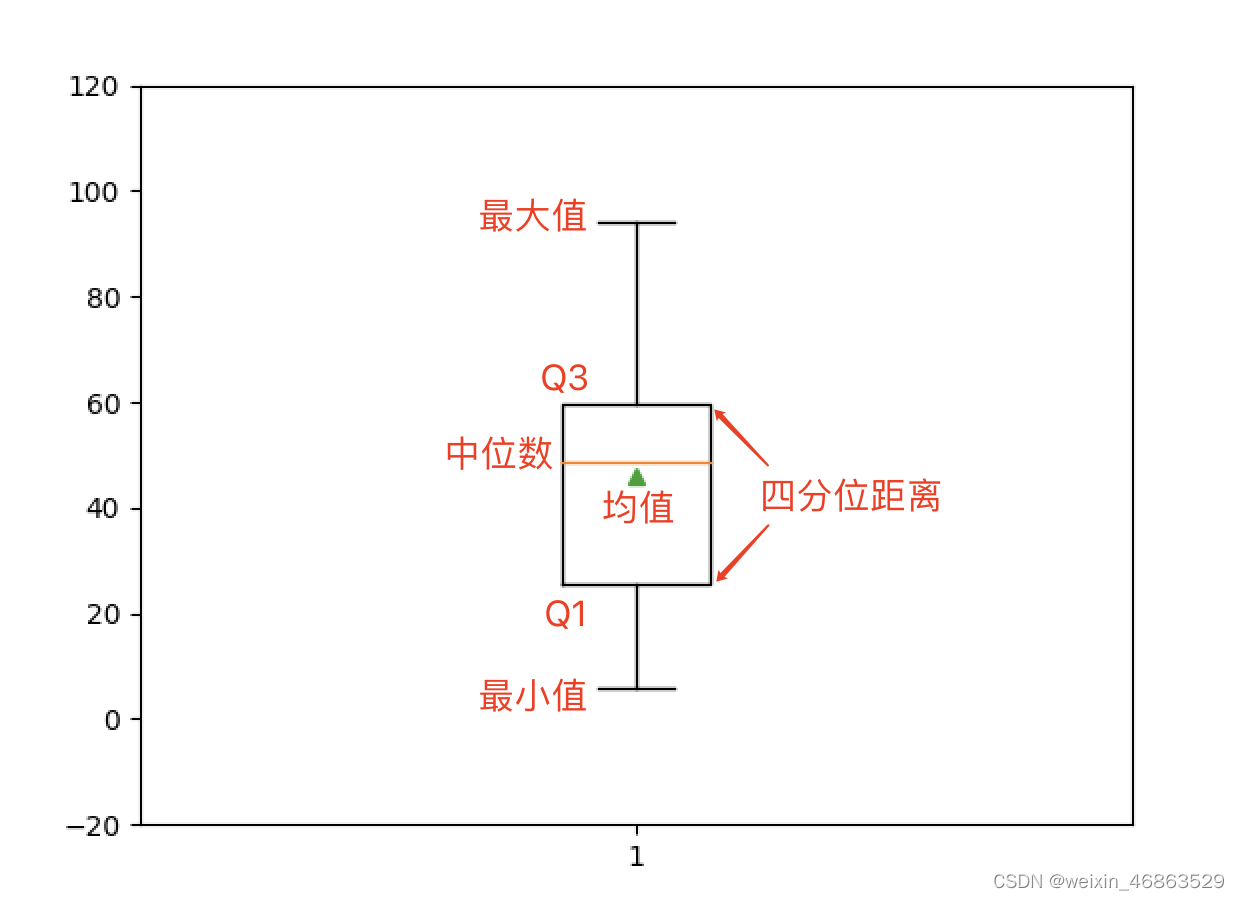
绘制箱线图。

箱线图又称为盒须图，是显示一组数据分散情况的统计图，因形状如箱子而得名。它主要用于反映原始数据分布的特征，还可以进行多组数据分布特征的比较。

代码：

plt.boxplot(array1, showmeans=True)
plt.ylim([-20, 120])
plt.show()

输出：

值得注意的是，对于二维或更高维的数组，在获取描述统计信息时，可以通过名为axis的参数指定均值、方差等运算是沿着哪一个轴来执行，axis参数不同，执行的结果可能是大相径庭的，如下所示。

代码：

array2 = np.random.randint(60, 101, (5, 3))
array2

输出：

array([[72, 64, 73],
       [61, 73, 61],
       [76, 85, 77],
       [97, 88, 90],
       [63, 93, 82]])

代码：

array2.mean()

输出：

77.0

代码：

array2.mean(axis=0)

输出：

array([73.8, 80.6, 76.6])

代码：

array2.mean(axis=1)

输出：

array([69.66666667, 65.        , 79.33333333, 91.66666667, 79.33333333])

代码：

array2.max(axis=0)

输出：

array([97, 93, 90])

代码：

array2.max(axis=1)

输出：

array([73, 73, 85, 97, 93])

再看看绘制箱线图，对于二维数组每一列都会产生一个统计图形，如下所示。

代码：

plt.boxplot(array2, showmeans=True)
plt.ylim([-20, 120])
plt.show()

输出：

说明：箱线图中的小圆圈用来表示离群点，也就是大于 $\small{Q_3 + 1.5 \times IQR}$ 或小于 $\small{Q_1 - 1.5 \times IQR}$ 的值。公式中的常量1.5可以通过绘制箱线图的boxplot函数的whis参数进行修改，常用的值是1.5和3，修改为3通常是为了标识出极度离群点。

需要说明的是，NumPy 的数组对象并没有提供计算几何平均值、调和平均值、去尾平均值等的方法，如果有这方面的需求，可以使用名为 scipy 的三方库，它的stats模块中提供了这些函数。此外，该模块还提供了计算众数、变异系数、偏态、峰度的函数，代码如下所示。

代码：

from scipy import stats

print(np.mean(array1))                # 算术平均值
print(stats.gmean(array1))            # 几何平均值
print(stats.hmean(array1))            # 调和平均值
print(stats.tmean(array1, [10, 90]))  # 去尾平均值
print(stats.variation(array1))        # 变异系数
print(stats.skew(array1))             # 偏态系数
print(stats.kurtosis(array1))         # 峰度系数

输出：

46.0
36.22349548825599
24.497219530825497
45.0
0.5547526228777941
0.11644192634527782
-0.7106251396024126

其他相关方法概述

all() / any()方法：判断数组是否所有元素都是True / 判断数组是否有为True的元素。
astype()方法：拷贝数组，并将数组中的元素转换为指定的类型。
reshape()方法：调整数组对象的形状。
dump()方法：保存数组到二进制文件中，可以通过 NumPy 中的load()函数从保存的文件中加载数据创建数组。

代码：
```
array.dump('array1-data')
array3 = np.load('array1-data', allow_pickle=True)
array3
```
输出：
```
array([46, 51, 15, 42, 53, 71, 20, 62,  6, 94])
```
tofile()方法：将数组对象写入文件中。
```
array1.tofile('res/array.txt', sep=',')
```
fill()方法：向数组中填充指定的元素。
flatten()方法：将多维数组扁平化为一维数组。

代码：
```
array2.flatten()
```
输出：
```
array([1, 2, 3, 4, 5, 6, 7, 8, 9])
```
nonzero()方法：返回非0元素的索引。
round()方法：对数组中的元素做四舍五入操作。

sort()方法：对数组进行就地排序。

代码：

array1.sort()
array1

输出：

array([ 6, 15, 20, 42, 46, 51, 53, 62, 71, 94])

swapaxes()和transpose()方法：交换数组指定的轴和转置。

代码：

array2.swapaxes(0, 1)

输出：

array([[1, 4, 7],
       [2, 5, 8],
       [3, 6, 9]])

代码：

array2.transpose()

输出：

array([[1, 4, 7],
       [2, 5, 8],
       [3, 6, 9]])

tolist()方法：将数组转成 Python 中的list。

代码：

print(array2.tolist())
print(type(array2.tolist()))

输出：

[[1, 2, 3], [4, 5, 6], [7, 8, 9]]
<class 'list'>

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1841824.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！