目录
前言
一、概率与统计基础
二、统计模型
三、Matlab统计工具箱
四、实例示范:市场调查分析
步骤 1:数据导入
步骤 2:数据可视化
步骤 3:建立多元线性回归模型
步骤 4:模型验证
步骤 5:模型应用
实例总结
总结
前言
统计模型是通过概率和统计学方法描述数据分布和关系的模型,广泛应用于数据分析、市场调查、预测等领域。本文将详细介绍统计模型的基础概念、常见类型和应用实例。
一、概率与统计基础
- 随机变量
- 随机变量是取不同数值的变量,每个数值对应一个概率。共有两类随机变量:离散型和连续型。
% 生成均匀分布的离散随机变量
x = randi([1, 6], 1, 100); % 模拟掷骰子 100 次
% 生成正态分布的连续随机变量
y = randn(1, 100); % 生成 100 个标准正态分布的样本
- 概率分布
- 概率分布是随机变量的取值及其概率的分布。常见的概率分布包括均匀分布、正态分布、泊松分布等。
% 均匀分布
uniform_dist = makedist('Uniform', 'lower', 0, 'upper', 1);
% 正态分布
normal_dist = makedist('Normal', 'mu', 0, 'sigma', 1);
% 泊松分布
poisson_dist = makedist('Poisson', 'lambda', 3);
- 样本统计量
- 样本统计量是从数据样本中计算出的统计特征,包括均值、方差、中位数等。
data = randn(1, 100); % 生成 100 个标准正态分布的样本
mean_val = mean(data); % 计算均值
var_val = var(data); % 计算方差
median_val = median(data); % 计算中位数
- 假设检验
- 假设检验用于检验样本数据是否符合某一假设,包括t检验、卡方检验等。
% 生成标准正态分布的数据
data = randn(1, 100);
% 进行单样本 t 检验
[h, p] = ttest(data);
% 卡方检验
obs = [10, 20, 30];
exp = [15, 15, 30];
[h, p] = chi2gof(obs, 'Expected', exp);
以下表格总结了常见的概率与统计基础操作:
| 操作 | 示例 | 说明 |
|---|---|---|
| 生成随机变量 | x = randi([1, 6], 1, 100); | 生成离散的随机变量 |
| 概率分布 | normal_dist = makedist('Normal',...); | 生成正态分布的概率分布对象 |
| 计算样本统计量 | mean_val = mean(data); | 计算数据的均值 |
| 假设检验 | [h, p] = ttest(data); | 进行单样本 t 检验 |
二、统计模型
统计模型是通过概率和统计方法描述数据分布和关系的模型。以下是几种常见的统计模型及其应用。
- 回归分析
- 回归分析用于研究自变量与因变量之间的关系,最常见的是线性回归。
% 线性回归 示例
x = [1, 2, 3, 4, 5];
y = [2, 4, 6, 8, 10];
model = fitlm(x, y);
disp(model);
- 方差分析(ANOVA)
- 方差分析用于比较多个组的均值是否存在显著差异。
% 单因素方差分析 示例
group = [1, 1, 1, 2, 2, 2, 3, 3, 3];
data = [5, 6, 7, 15, 16, 17, 8, 9, 10];
p = anova1(data, group);
- 时间序列分析
- 时间序列分析用于处理时间序列数据,常见的方法包括自回归模型(AR)、移动平均模型(MA)等。
% 自回归模型 (AR) 示例
data = load('airline.mat');
ts = iddata(data.airline, [], 1);
model = ar(ts, 4);
present(model);
- 贝叶斯统计模型
- 贝叶斯统计模型利用贝叶斯公式进行统计推断,广泛应用于机器学习、预测分析等领域。
% 贝叶斯估计 示例
prior = makedist('Normal', 'mu', 0, 'sigma', 1);
data = [1.2, 0.9, 1.1, 1.5, 1.0];
posterior = fitdist(data', 'Kernel', 'Kernel', 'normal', 'Width', 0.3);
以下表格总结了常见的统计模型及其示例:
| 模型类型 | 示例 | 说明 |
|---|---|---|
| 回归分析 | fitlm(x, y); | 构建线性回归模型 |
| 方差分析 | p = anova1(data, group); | 进行单因素方差分析 |
| 时间序列分析 | model = ar(ts, 4); | 构建自回归模型 |
| 贝叶斯统计模型 | fitdist(data', 'Kernel',...); | 构建贝叶斯估计模型 |
三、Matlab统计工具箱
Matlab 提供了强大的统计工具箱,内置了多种统计函数和方法,便于我们进行数据分析、建模和可视化。
- 统计函数
- 工具箱提供了丰富的统计函数,如描述性统计、随机抽样、假设检验等。
% 描述性统计
data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
stats = summary(data);
% 随机抽样
sample = randsample(data, 5);
% 假设检验
[h, p] = ttest(data);
- 数据分析
- 工具箱支持多种数据分析方法,如聚类分析、主成分分析(PCA)等。
% 聚类分析
data = rand(100, 2);
idx = kmeans(data, 3);
% 绘制聚类图
figure;
gscatter(data(:,1), data(:,2), idx);
title('K-means Clustering');
% 主成分分析 (PCA)
coeff = pca(data);
- 数据可视化
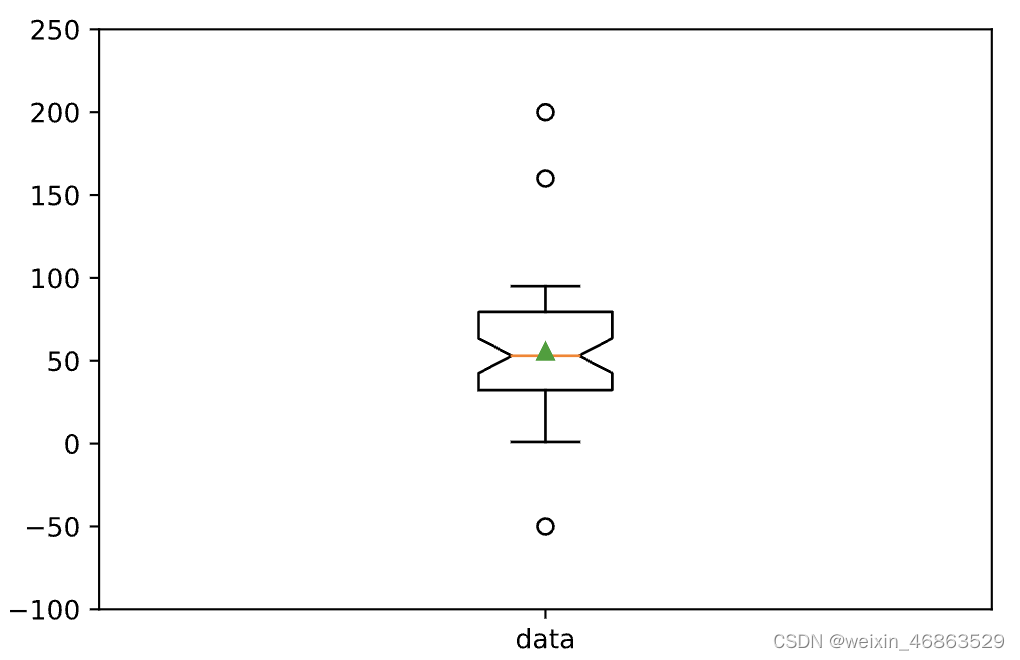
- 工具箱提供了丰富的数据可视化函数,如箱线图、散点图、热图等。
% 箱线图
figure;
boxplot(data);
title('Box Plot');
% 散点图
figure;
scatter(data(:,1), data(:,2));
title('Scatter Plot');
% 热图
figure;
heatmap(data);
title('Heat Map');
以下表格总结了 Matlab 统计工具箱中的常用函数:
| 功能 | 函数 | 说明 |
|---|---|---|
| 描述性统计 | summary(data); | 计算描述性统计量 |
| 随机抽样 | randsample(data, n); | 从数据中随机抽样 |
| 假设检验 | [h, p] = ttest(data); | 进行 t 检验 |
| 聚类分析 | idx = kmeans(data, k); | 进行 K-means 聚类分析 |
| 主成分分析 | coeff = pca(data); | 进行主成分分析 |
| 箱线图 | boxplot(data); | 绘制箱线图 |
| 散点图 | scatter(data(:,1), data(:,2)); | 绘制散点图 |
| 热图 | heatmap(data); | 绘制热图 |
四、实例示范:市场调查分析
为了更加全面地理解统计模型,我们通过一个市场调查分析的实例展示从数据导入、分析到结果可视化的过程。假设我们有一组关于某产品市场需求的调查数据,包含消费者的年龄、收入和对产品的满意度评分。我们的任务是通过统计模型分析这组数据,找出影响满意度的主要因素,并进行可视化展示。
步骤 1:数据导入
假设数据存储在一个 CSV 文件 market_survey.csv 中,内容如下:
Age,Income,Satisfaction
25,30000,7
32,45000,8
45,60000,6
23,35000,9
35,50000,7
50,65000,6
60,70000,5
40,55000,7
48,63000,6
30,40000,8
% 导入数据到表格
data = readtable('market_survey.csv');
age = data.Age;
income = data.Income;
satisfaction = data.Satisfaction;
步骤 2:数据可视化
在进行回归分析之前,我们可以先对数据进行可视化,检查数据的分布和趋势。
% 绘制散点图
figure;
subplot(1, 2, 1);
scatter(age, satisfaction, 'filled');
title('Satisfaction vs Age');
xlabel('Age');
ylabel('Satisfaction');
grid on;
subplot(1, 2, 2);
scatter(income, satisfaction, 'filled');
title('Satisfaction vs Income');
xlabel('Income');
ylabel('Satisfaction');
grid on;
步骤 3:建立多元线性回归模型
使用 fitlm 函数建立多元线性回归模型,分析年龄和收入对满意度的影响。
% 建立多元线性回归模型
X = [age, income];
mdl = fitlm(X, satisfaction);
% 显示模型参数
disp(mdl);
步骤 4:模型验证
我们可以通过绘制回归图和残差图来验证模型的效果,并计算模型的常规统计指标来判断模型的拟合度。
% 绘制回归图
figure;
plot(mdl);
title('Satisfaction Regression Model');
xlabel('Predictors');
ylabel('Satisfaction');
grid on;
% 绘制残差图
figure;
plotResiduals(mdl, 'fitted');
title('Residuals of the Regression Model');
grid on;
步骤 5:模型应用
通过训练好的模型,我们可以预测新的消费者数据,例如给定某个消费者的年龄和收入,预测其对产品的满意度。
% 预测新的消费者满意度
new_age = 28;
new_income = 48000;
new_data = [new_age, new_income];
predicted_satisfaction = predict(mdl, new_data);
disp(['Predicted satisfaction for age ' num2str(new_age) ' and income $' num2str(new_income) ': ' num2str(predicted_satisfaction)]);
实例总结
通过上述步骤,我们完成了市场需求数据的导入、可视化、模型建立、验证和应用。以下是该实例的总结:
| 步骤 | 说明 | 示例 |
|---|---|---|
| 数据导入 | 从CSV文件中导入数据 | readtable('market_survey.csv'); |
| 数据可视化 | 绘制散点图,检查数据分布和趋势 | scatter(age, satisfaction, 'filled'); |
| 建立模型 | 使用多元线性回归模型分析数据 | mdl = fitlm(X, satisfaction); |
| 模型验证 | 绘制回归图和残差图,计算统计指标 | plot(mdl); plotResiduals(mdl, 'fitted'); |
| 模型应用 | 使用模型预测新的消费者满意度 | predict(mdl, new_data); |
总结
本文详细介绍了统计模型的基础概念和方法,包括概率与统计的基础知识、常见统计模型和 Matlab 统计工具箱的应用。通过市场调查分析的实际案例,展示了如何在 Matlab 中导入数据、进行可视化和建模分析。






![[Linux] 版本控制](https://img-blog.csdnimg.cn/direct/570c180e4bc14638a6fb56c6086a17e1.png)