【数据结构】选择题

news2024/11/23 1:06:09

在数据结构中，从逻辑上可以把数据结构分为（线性结构和非线性结构）
当输入规模为n时，下列算法渐进复杂性中最低的是（）
时间复杂度
某线性表采用顺序存储结构，每个元素占4个存储单元，首地址为100，则第12个元素的存储地址为（144）
在单链表中，若p所指的结点不是最后结点，在p之后插入s所指结点，则执行（）

s->next=p->next; p->next=s;

设h为不带头结点的单向链表。在h的头上插入一个新结点t的语句是（）

t->next=h; h=t;

链表的适用场合：线性表在（线性表需经常插入或删除数据元素）情况下适合采用链式存储结构
设一个堆栈的入栈顺序是1、2、3、4、5。若第一个出栈的元素是4，则最后一个出栈的元素必定是（1或者5）
若元素a、b、c、d、e、f依次进栈，允许进栈、退栈操作交替进行，但不允许连续三次进行退栈工作，则不可能得到的出栈序列是（a f e d c b）
若已知一队列用单向链表表示，该单向链表的当前状态（含3个对象）是：1->2->3，其中x->y表示x的下一节点是y。此时，如果将对象4入队，然后队列头的对象出队，则单向链表的状态是（2->3->4）
在一个不带头结点的非空链式队列中,假设f和r分别为队头和队尾指针,则删除结点的运算是( f=f->next;)
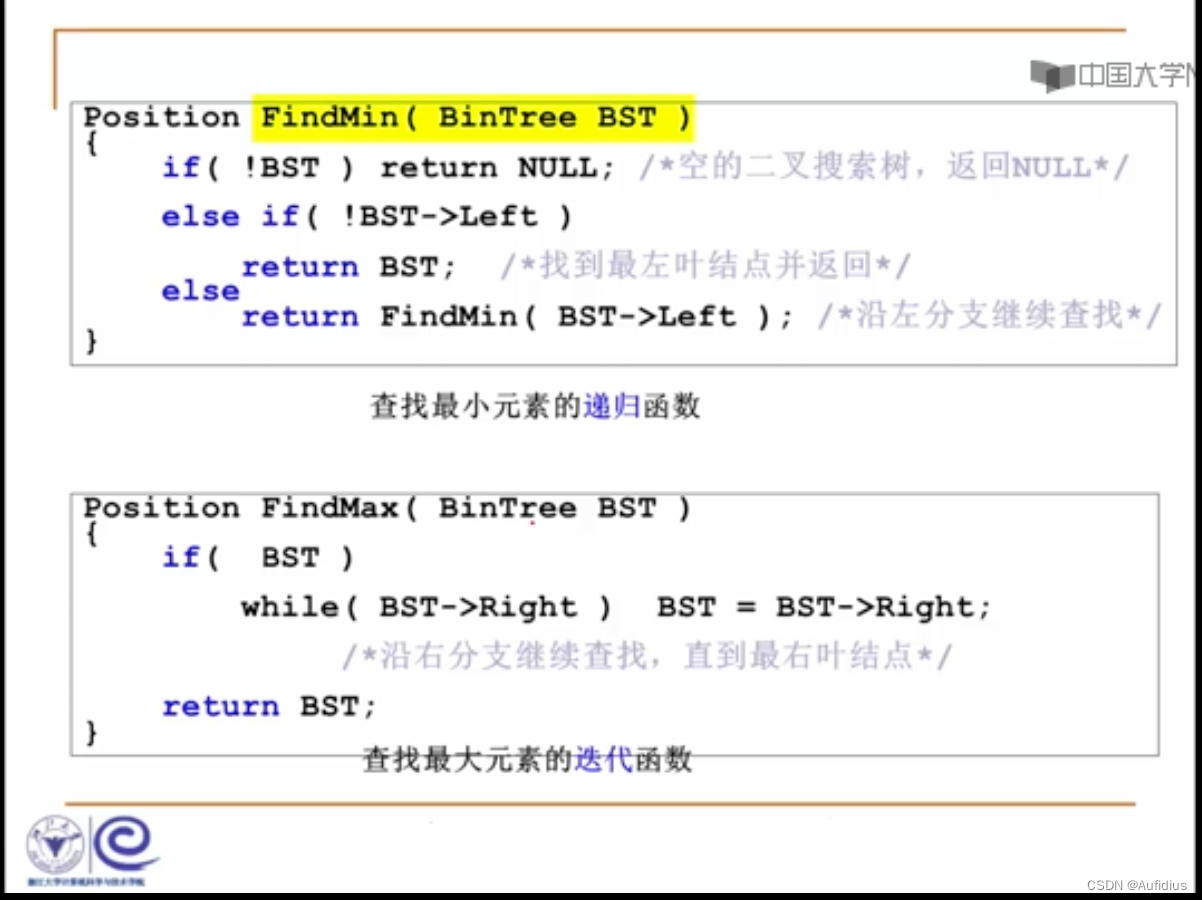
已知二叉树的前序遍历序列为 ABDCEFG，中序遍历序列为 DBCAFEG，则后序遍历序列为（DCBFGEA）
完全二叉树的第4层有1个节点，该完全二叉树总计有（8）个节点
深度为k的完全二叉树的第k层至少有（1）个结点
具有65个结点的完全二叉树其深度为（根的深度为1）：7
一个高度为h的满二叉树共有n个结点，其中有m个叶子结点，则有（ n = 2m - 1 ）成立
一棵完全二叉树上有62个结点，其中叶子结点的个数是（31）
根据使用频率为5个字符设计的哈夫曼编码不可能是（100,11,10,1,0 ）
在哈夫曼树中，任何一个结点它的度都是（0或2）
设给定权值总数有n 个，其哈夫曼树的结点总数为( 2n-1)
对 n 个互不相同的符号进行哈夫曼编码。若生成的哈夫曼树共有 115 个结点，则 n 的值是（58）
一段文本中包含对象{a,b,c,d,e}，其出现次数相应为{3,2,4,2,1}，则经过哈夫曼编码后，该文本所占总位数为（27）
无向连通图的最小生成树（有一个或多个）
用邻接表表示图进行广度优先遍历时，通常借助（队列）来实现算法
在存储数据时，通常不仅要存储各数据元素的值，而且还要存储（数据元素之间的关系）
算法分析的两个主要方面是（空间复杂度和时间复杂度）
用数组表示线性表的优点是（便于随机存取）
带头结点的单链表h为空的判定条件是（h->next == NULL;）
假设有5个整数以1、2、3、4、5的顺序被压入堆栈，且出栈顺序为3、5、4、2、1，那么为了获得这样的输出，堆栈大小至少为（4）
设一个栈的输入序列是1、2、3、4、5，则下列序列中，是栈的合法输出序列的是（A）
为解决计算机主机与打印机之间速度不匹配问题，通常设置一个打印数据缓冲区，主机将要输出的数据依次写入该缓冲区，而打印机则依次从该缓冲区中取出数据。该缓冲区的逻辑结构应该是（队列）
二叉树中第5层（根的层号为1）上的结点个数最多为（16）
完全二叉树的第5层有3个节点，该完全二叉树总计有多少个节点（18）
深度为k的完全二叉树至少有(1)个结点，至多有(2)个结点
在一棵完全二叉树中，其根的序号为1，（　）可判定序号为 p和q 的两个结点是否在同一层
如果一个完全二叉树最底下一层为第六层（根为第一层）且该层共有8个叶结点，那么该完全二叉树共有（39）个结点
设有13个值，用它们构成一棵哈夫曼树，则该哈夫曼树共有结点数是（25）
设哈夫曼树中有199个结点，则该哈夫曼树中有（100）个叶子结点
观察下面的数据结构
数据结构可以从逻辑上分成 ▁▁▁▁▁ 两大类
以下关于数据结构的说法中错误的是（）。
计算机所处理的数据一般具有某种关系，这是指（数据元素与数据元素之间存在的某种关系）
在计算机的存储器中表示时，逻辑上相邻的两个元素对应的物理地址也是相邻的，这种存储结构称之为（顺序存储结构）
数据元素在计算机存储器内表示时，物理相对位置和逻辑相对位置相同并且是连续的，称之为（顺序存储结构）
在数据结构中，与所使用的计算机无关的是数据的（逻辑）结构
通常要求同一逻辑结构中的所有数据元素具有相同的特性，这意味着（不仅数据元素所包含的数据项的个数要相同，而且对应的数据项的类型要一致）
以下属于顺序存储结构优点的是（A）
被计算机加工的数据元素不是孤立的，它们彼此之间一般存在某种关系，通常把数据元素之间的这种关系称为（B）
与数据元素本身的形式、内容、相对位置、个数无关的是数据的（C）
数据在计算机内存中的表示是指（A）
算法的时间复杂度取决于（C）
下面程序的时间复杂度为（A）
执行下面程序段时，执行S语句的频度为（D）
算法的时间复杂度取决于（ D）
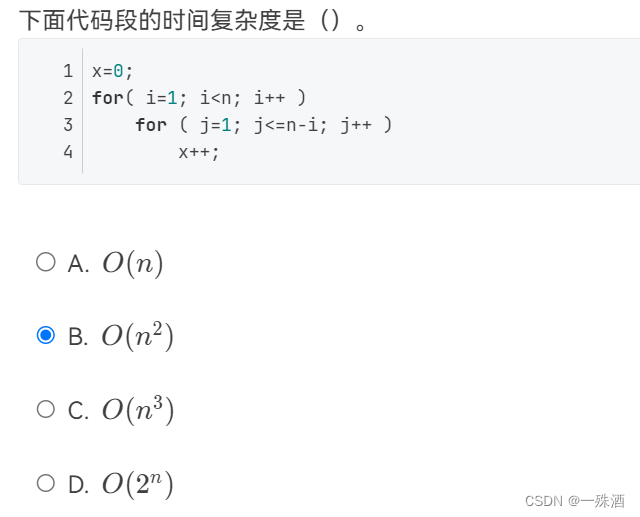
下面代码段的时间复杂度是（）