0、前言
深度优先搜索是DFS(Depth Frst Search),其实就是前面所讲过的回溯算法,它的特点和它的名字一样,首先在一条路径上不断往下(深度)遍历,获得答案之后再返回,再继续往下遍历。这也是递归的思想,所以这也是为什么回溯算法通常都是用递归来写,而下面的BFS由于不是这种思路从而没有用递归。
广度优先算法(Breath First Search)其实和深度优先算法是一对兄弟,因为它们的解空间都是树形解空间,并且都是在求解过程中 动态生成树形解空间。广度优先算法在于,它在动态生成解空间从而获得答案时,是从一层一层(广度的)取构建并搜索答案。
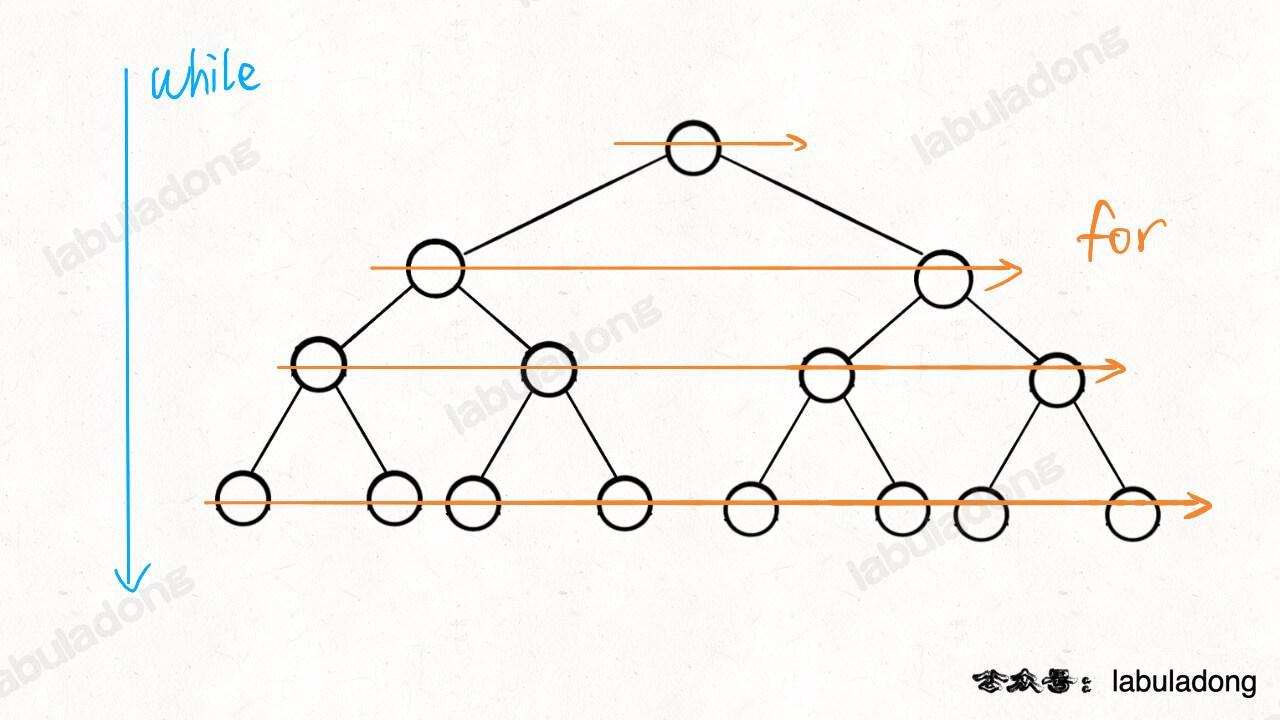
它的核心思想是:把问题的求解抽象为一个图,从一个起点开始,向四周去扩散,不断扩散直至求得答案。
BFS和DFS的主要区别在于:
- 在查找路径问题上,BFS查找出来的路径是最短的
- BFS的空间复杂度要比DFS高(这也是BFS的代价)
一、算法框架
知道它的核心思想之后,其实我们就可以写出它的算法框架,本质就是遍历图:
//计算起点start到终点target的最短距离
int BFS(Node start, Node target) {
queue<Node> q; //核心数据结构
set<Node> visited; //避免走回头路
q.push(start); //将起点加入队列
visited.insert(start);
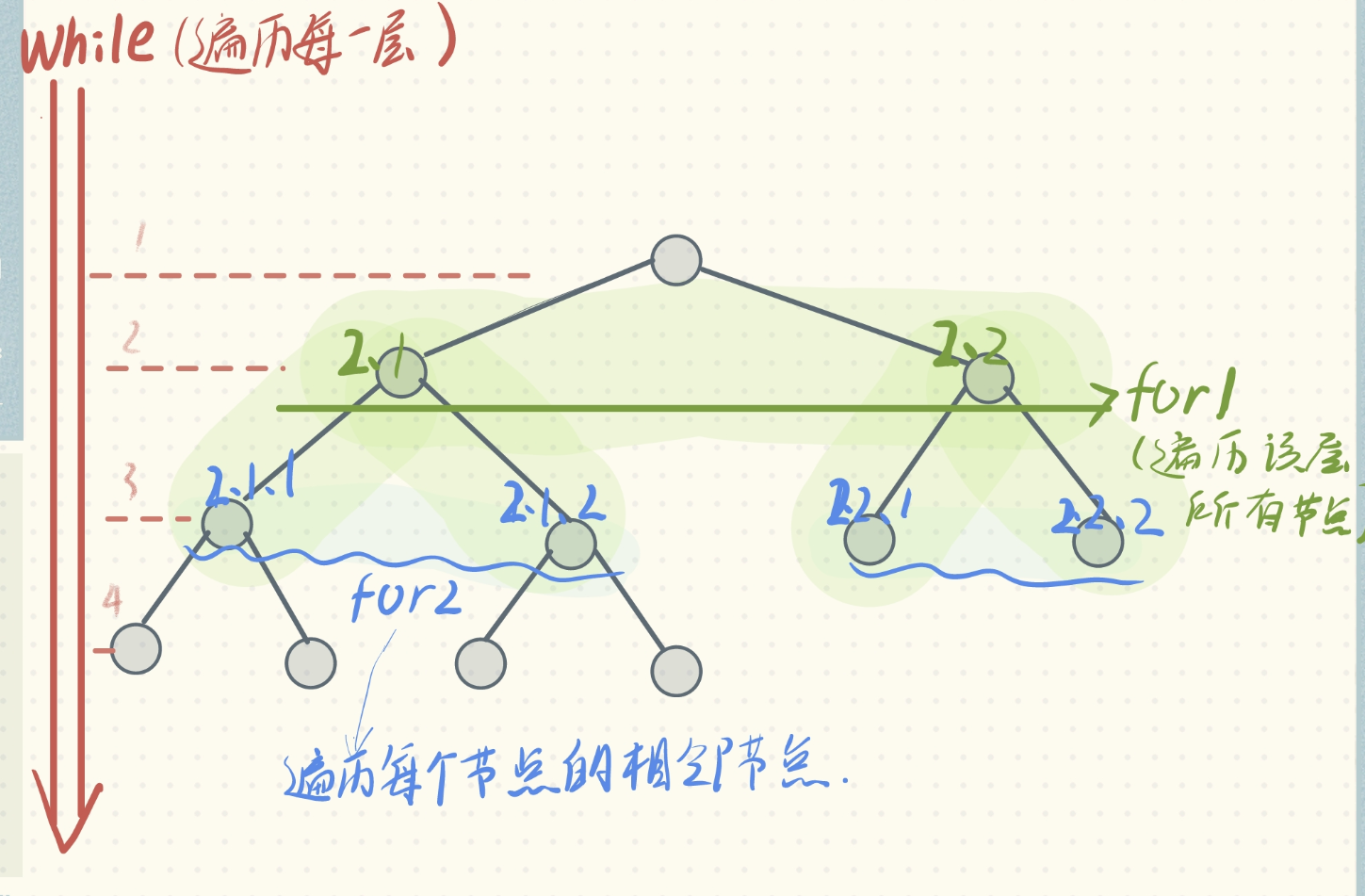
//走完一次完整的下面1,2,3循环,代表以当前层节点完整的依次向外扩散了一层
//循环1:从起点开始,不断将当前队列中所有节点向四周扩散
while (!q.empty()) {
int sz = q.size();
//2:循环2:队列中所有节点依次往外扩散一层
for (int i = 0; i < sz; i++) {
Node cur = q.front();
q.pop();
if (cur == target)
return step;
//循环3:把当前层的队列节点往外扩散一层,并把扩散得到的加入队列
for (Node x : cur.adj()) {
if (visited.count(x) == 0) {
q.push(x);
visited.insert(x);
}
}
}
}
// 如果走到这里,说明在图中没有找到目标节点
}
- 其中
Queue<Node> q是队列,存储当前遍历层和即将遍历层的节点,是BFS的核心数据结构; cur.adj()泛指与当前遍历到的这个节点cur相邻的节点(也就是与cur相连的下一层的节点,不如二维数组中cur上下左右四个位置就是相邻节点);visited的作用防止走回头路;(但是对于二叉树这种结构,没有子节点到父节点的指针,不会走回头路也就不需要visited)
二、题目
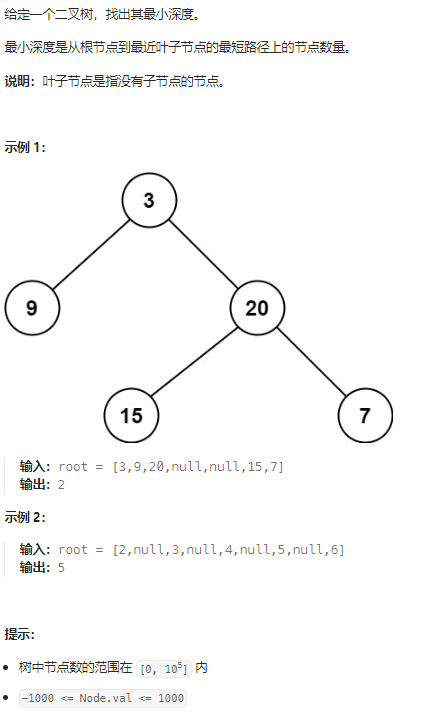
2.1:二叉树的最小高度
1.题目
🔗111. 二叉树的最小深度
2.思路
这道题就是非常典型和简单的BFS算法,我们只需要把上面算法框架中的cur == target找到目标答案的位置改成找到叶子节点:cur.left == null && cur.right == null即可
3.代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minDepth(TreeNode* root) {
if(root == nullptr) return 0;
queue<TreeNode*> q; //核心数据结构,用来存储当前节点
int depth = 0; //记录当前层的深度
//将第一层输入队列:即起点
q.push(root);
//从当前层逐层扩散和遍历:循环1:遍历层
while(!q.empty()){
//获取当前层所以节点数量
int sz = q.size();
depth++;
//循环2:遍历当前层的所有节点
for(int i = 0; i < sz; i++){
TreeNode* cur = q.front();
q.pop();
//判断当前遍历到的这个节点释放符合答案需求
if(cur->left == nullptr && cur->right == nullptr)
return depth;
//循环3:以当前层的当前节点往外再扩一层,并把扩散得到的下一层节点加入队列
//这里就已经确定了是左右孩子两个相邻节点,就不写循环了
if(cur->left!=nullptr) q.push(cur->left);
if(cur->right!=nullptr) q.push(cur->right);
}
}
return 0;
}
};
2.2:解开密码锁的最少次数
1.题目
🔗752. 打开转盘锁

2.思路
- 分析:题目要求我们从
0000开始,根据旋转规则,每次只能向上或向下旋转一次四个数位的其中一位,通过不断的旋转直到四位数字为最终答案target。 - 关键:把问题抽象成一张图,当前4位数字密码为节点,通过当前密码状态选择一个数位向上或向下旋转一次得到下一个四位数(节点),每个节点可以实现
2x2x2x2 = 8种选择得到下一个节点;即:该问题抽象为一张图,每个节点有8个相邻节点,我们需要从起始节点"0000"以最短路径寻找到我们的目标节点target(注意还有限制条件)
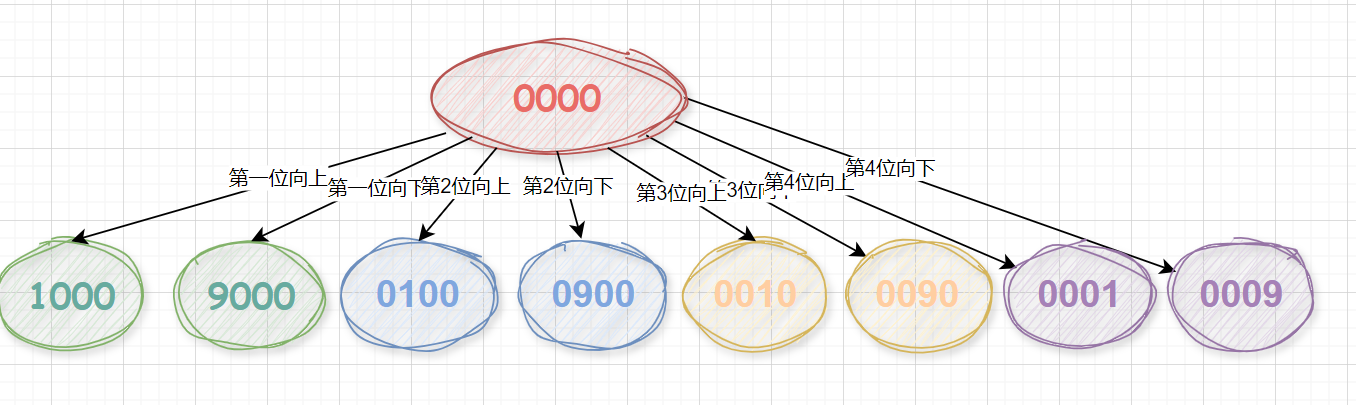
有了上述分析后,大概有对这个题有了一个这个题的把握和认识,但是其实还有很多细节没有分析到。当然,一下子其实分析不到所有的细节是很正常,我们一步一步来,慢慢完善。
- 首先,我们先不考虑【死亡密码】的限制,想一想,从
"0000"出发,穷举出所有密码的可能,我们需要怎么做;也就是说,从"0000"出发,每个节点有8个相邻,我们以BFS遍历出所有密码
//BFS框架,打印出所有可能的密码
void BFS(string target){
queue<string> q;
q.push("0000");
while(!q.empty()){
int sz = q.size();
//将当前层(也就是当前队列)中节点向下一层(周围)扩散
for(int i = 0; i < sz; i++){
//获取当前节点
string cur = q.front(); q.pop();
//判断是否达到终点
cout << cur << endl;
//将当前节点相邻的周围节点(也就是下一层的)加入到队列
for(int j = 0; j < 4; j++){
//当前位向上拨
string up = plusOne(cur, j);
q.push(up);
//当前位向下拨
string down = minusOne(cur, j);
q.push(down);
}
}
//在这里增加步数
}
}
上面代码中的plusOne和minusOne函数的代码如下:
string plusOne(string s, int j) {
if (s[j] == '9') s[j] = '0';
else s[j] += 1;
return s;
}
string minusOne(string s, int j) {
if (s[j] == '0') s[j] = '9';
else s[j] -= 1;
return s;
}
- 当然,上述代码还有很多问题
- 首先,会走回头路,比如从
"0000"到"1000"但是"1000"的8个相邻点里面又有"0000"这样下去会产生死循环。这个时候就需要额外加一个集合数据结构visited,记录下来已经走过的节点,在往下扩散的时候(也就是往队列里面加元素的时候)进行判断,是否已经遍历过。 - 没有终止条件,这个其实挺好改的,只需要在遍历到那个具体的节点的时候加一个判断条件,遇到
target结束循环并返回即可。 - 没有对限制条件(不能出现死亡密码)的处理
3.代码
class Solution {
public:
string plusOne(string s, int j) {
if (s[j] == '9') s[j] = '0';
else s[j] += 1;
return s;
}
string minusOne(string s, int j) {
if (s[j] == '0') s[j] = '9';
else s[j] -= 1;
return s;
}
int openLock(vector<string>& deadends, string target) {
unordered_set<string> deads; //记录限制条件:需要跳过的死亡密码
for(string s : deadends){
deads.insert(s);
}
//记录已经穷举过的密码,防止走回头路
unordered_set<string> visited;
queue<string> q;
int step = 0;
//从起点开始进行BFS
q.push("0000");
visited.insert("0000");
while(!q.empty()){
int sz = q.size();
for(int i = 0; i < sz; i++){
string cur = q.front();
q.pop();
if(deads.count(cur)) continue; //分支限界,在遍历到这个节点的时候限制就行
//判断是否达到终止条件
if(cur == target) return step;
for(int j = 0; j < 4; j++){
string left = plusOne(cur,j);
if(!visited.count(left) ){
q.push(left);
visited.insert(left);
}
string right = minusOne(cur,j);
if(!visited.count(right)) {
q.push(right);
visited.insert(right);
}
}
}
step++;
}
return -1;
}
};
2.3:布线问题
1.题目
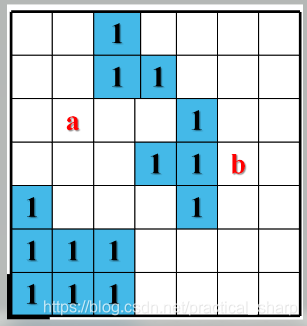
印刷电路板将布线区域划分成n*m个方格阵列,精确的电路布线问题要求确定连接方格a的中点到方格b的中点的最短布线问题。在布线时,电路只能沿着直线或直角布线。为了避免线路相交,已布了线的方格做了封锁标记,其他线路不允许穿过被封锁的方格。
2.思路
- 分析:其实这个题就是有障碍物的迷宫问题。本质上也是抽象为图问题,格子上每一个点的坐标位置就是一个节点,一个节点可以往上下左右4个方向行走到达其他位置(节点);注意限制条件:不能在障碍物(也就是题目所说的封锁方格)处进行遍历,所以遇到该限制条件就跳过且不扩展该样的节点。
- 关键:
- 用一个队列来进行BFS搜索,找到起点位置到终点位置的最短路径
- 用一个二维布尔数组
visited来存储对应位置处方格是否被访问过(避免走回头路) - 用一个二维数组来记录封锁方格(其实就是存储初始棋盘
grid[][]) - 如果需要记录最终得到的那个最短路径,可以设置一个以
pair<int, int>为元素的二维数组,记录(x,y)位置是由parent[x][y]得来的(记录路径,能从目标节点反推回去完整路径)
3.代码
#include <iostream>
#include <vector>
#include <queue>
#include <tuple>
using namespace std;
//定义节点可以扩展的四个方向:上下左右{x,y}
vector< pair<int, int> > dirs ={{-1,0}, {1,0}, {0,-1}, {0, 1}};
/*辅助函数,判断该节点是否合法
1. 不能超过整个迷宫(电线板)边界
2. 不能被访问过(不能走回头路)
3. 不能是封锁节点(即迷宫里的障碍物
*/
bool isValid(int x, int y, int n, int m, vector<vector<int>>& grid, vector <vector<bool>>& visited){
return x >= 0 && x <n && y>=0 && y < m && grid[x][y] != -1 && !visited[x][y];
}
//BFS算法求解最短路径并标记路径节点
vector <vector<int>> shortestPath(vector<vector<int>>& grid, pair<int, int> Start, pair<int, int> End){
int n = grid.size();
int m = grid[0].size();
//队列,存储当前坐标和部署
queue<tuple<int, int, int>> q;
//已经访问节点的存储
vector<vector<bool>> visited(n, vector<bool>(m, false));
//记录当前节点是由哪个节点得来(记录路径)
vector<vector<pair<int, int>>> parent(n, vector<pair<int, int>>(m, make_pair(-1, -1)));
//将起点加入队列
q.push(make_tuple(Start.first, Start.second, 0));
visited[Start.first][Start.second] = true;
bool found = false; //标记是否找到,一旦找到,路径最短, 退出
while(!q.empty()){
int sz = q.size();
//遍历该层
for(int i = 0; i < sz; i++){
//先拿出当前节点
auto [cur_x, cur_y, steps] = q.front();
q.pop();
//可选:判断当前节点是否合理(其实没必要,起点肯定一般都是合理,保证在下面扩展的时候不添加不合理的即可
//判断是否达到终点
if( cur_x == End.first && cur_y == End.second){
found = true;
break;
}
//扩展四个方向
for(auto [dx, dy] : dirs){
int newX = cur_x + dx;
int newY = cur_y + dy;
//判断合法
if(isValid(newX, newY, n, m, grid, visited)){
q.push(make_tuple(newX, newY, steps+1));
visited[newX][newY] = true;
//记录父节点
parent[newX][newY] = make_pair(cur_x, cur_y);
}
}
}
}
if(found){
int x = End.first;
int y = End.second;
while(!(x == Start.first && y == Start.second)){
grid[x][y] = 1;
tie(x,y) = parent[x][y];
}
grid[Start.first][Start.second] = 1; //标记起点
}
return grid;
}
int main(){
//输入
int n, m;
cout << "请输入电路板的行数和列数:";
cin >> n >> m;
vector <vector<int>> grid (n, vector<int>(m, 0));
cout << "请输入电路版的状态(0为空,-1为封锁状态):"<<endl;
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
cin >> grid[i][j];
}
}
int startX, startY, endX, endY;
cout << "请输入起点坐标(x y):";
cin >> startX >> startY;
cout << "请输入终点坐标(x y):";
cin >> endX >> endY;
//BFS遍历
vector< vector<int> > res = shortestPath(grid, {startX, startY}, {endX, endY});
//输出结果
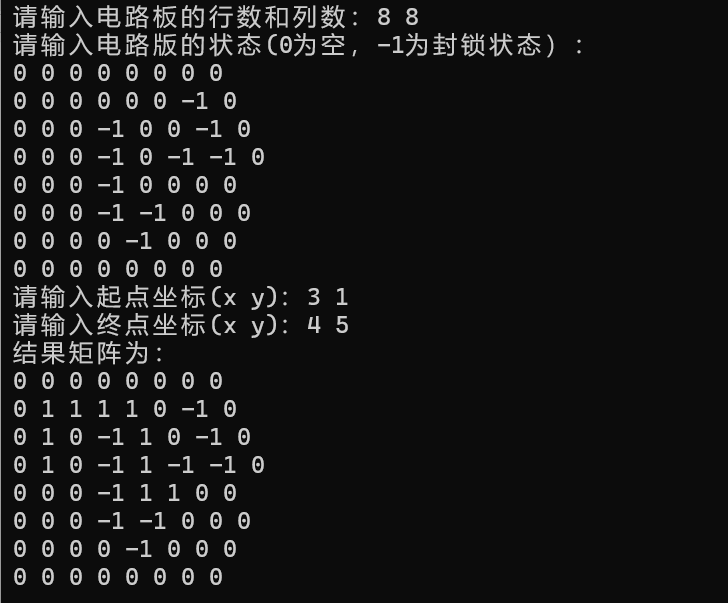
cout << "结果矩阵为:"<< endl;
for(const auto& row : res){
for(int cell : row){
cout << cell << " ";
}
cout << endl;
}
return 0;
}
end:本文参考
🔗labuladongBFS算法解题套路框架
🔗布线问题分支界限法求解