问题一(指数级选择)
从1~n这n个整数中任意选取多个,输出所有可能的选择方案。
首先想一下,在现实世界中,我们要如何解决这个问题。
应该是一个一个枚举,即每个数都可以有两个选择(选/不选)。共有种结果。
想一下,如何在“纸上”解决问题呢?不妨假设有3各数(分别为1、2、3)。
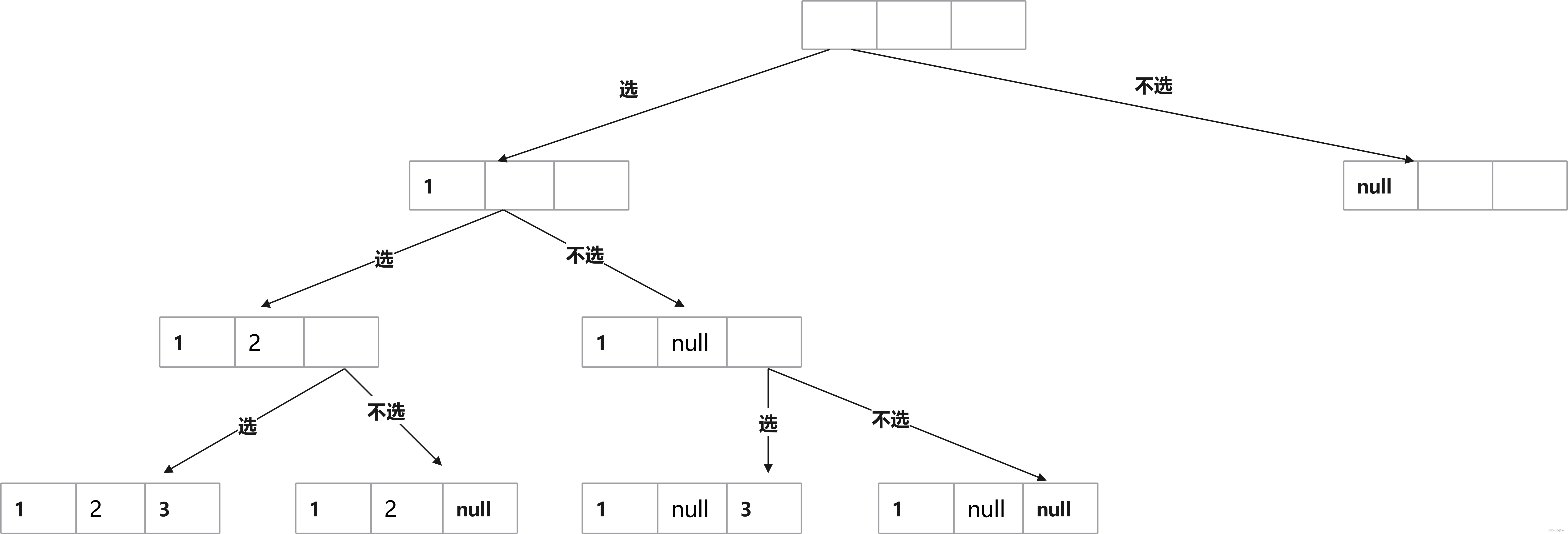
一共有3个位置,从第一个位置开始枚举选还是不选,这里只列出了一半。那么在编程语言上如何实现呢?
仔细想一下,实现这个业务逻辑需要什么?首先一定需要一个数组来存要存的n个数。还需要存每个位置的状态,即选/不选/不确定这3个状态。想一下,这不妨用一个数组来存,从下标1开始到下标n,每个可以存3个状态,最后遍历数组,根据存的内容输出。现在假设:
| 状态 | 标识 |
| 选 | 1 |
| 不选 | 0 |
| 未确定 | -1 |
那么如何通过编程语言来实现呢?
#include<iostream>
#include<algorithm>
#include<string>
#define N 10
using namespace std;
int arr[N];
int n;
int st[N];
void dfs(int x) //x表示当前枚举到了哪个位置
{
if(x>n)
{
for(int i=1;i<=n;i++)
{
if(st[i]==1)
{
cout<<i<<" ";
}
}
cout<<endl;
return ;
}
st[x] = 1; //第x层,即第x个位置,先选
dfs(x+1); //这层选完了,继续向下一层递进
st[x] = -1; //回溯
st[x] = 0;
dfs(x+1);
st[x]=-1;
}
int main()
{
cin>>n;
dfs(1);
return 0;
}package DFS;
import java.util.Scanner;
public class choice_num {
static int[] st;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("请输入数字:");
int n = sc.nextInt();
st = new int[n + 1];
dfs(1, n);
}
public static void dfs(int x, int n) {
if (x > n) {
for (int i = 1; i <= n; i++) {
if(st[i]==1) {
System.out.print(i + " ");
}
}
System.out.println();
return;
}
st[x] = 1;
dfs(x + 1, n);
st[x] = -1;
st[x] = 0;
dfs(x + 1, n);
st[x] = -1;
}
}可能刚开始有点看不懂,但是先这样理解:函数(方法)自己调用自己,就是为了向“数”的叶子出发,为什么可以自己调用自己呢,因为枚举有规律,上面的都是先“选”,到叶子节点(该return了),再返回到上一层,然后再“不选”。就像遍历一颗二叉树一样,先左边的,左边的遍历到底了,一层一层的返回遍历右边的。现在先记住这样,以后做题多了,应该可以慢慢理解。
问题二:(排列)
按照字典序输出自然数1到n所有不重复的排列。即n的全排列,要求产生的任一数字序列中不允许出现重复的数字。
现在再想一下,在现实世界中,我们要如何解决这个问题?

这也可以用枚举来试下,选第一个位置、再选第二个位置、最后是第三个位置。其中选第一个位置有3个分支(选法),第二个位置有2个,第三个位置有1个。
想一下如何用代码实现?这个题和上一个有所不同,因为上一个只要记录哪个位置选哪个没选就行了,但是这道题还要记录哪些数字可以选,哪些数字不可以选。比如上面的从第一个位置到第二个位置,1已经选完了,剩下2、3可供选择,这可以另开一个数组来记录哪些树可以选。比如(0表示不可选,1表示可选)。还要一个数组来记录排列的顺序。
来看代码:
C++
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
bool available[10];
int selected[10];
int n;
void dfs(int x) //到第x个位置,也是第x层
{
if(x>n)
{
for(int j=1;j<=n;j++)
{
cout<<selected[j]<<" ";
}
cout<<endl;
return ;
}
for(int i=1;i<=n ;i++) //每个位置都有可能选到n个数中的一个。从第一个开始选。
{
if(!available[i])
{
available[i] = true;
selected[x] = i;
dfs(x+1);
selected[x] = 0;//一点退出 dfs[x+1],就说明已经返回到它的上一层了。那就将这层的已选的清除,换成另一个。
available[i] = false;
}
}
}
int main()
{
cin>>n;
dfs(1);
return 0;
}注意这里的运行结果是:
3
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
我们发现这个有个规律,即每次都是从最后一个开始交换,这是因为在递归的时候,是从最后一层开始向上层回溯的。
JAVA
package DFS;
import java.util.Scanner;
public class arrange {
static boolean[] available = new boolean[11];
static int[] selected = new int[11];
static int n;
public static void dfs(int x) {
if (x > n) {
for (int j = 1; j <= n; j++) {
System.out.print(selected[j]+" ");
}
System.out.println();
return;
}
for (int i = 1; i <= n; i++) {
if (!available[i]) {
selected[x] = i;
available[i] = true;
dfs(x + 1);
selected[x] = 0;
available[i] = false;
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
dfs(1);
}
}其实,这里的for循环没有讲清除,即为什么dfs要套在for循环的里面呢?这个东西刚开始是没法判断的,刚开始想要实现在1~n中选一个没有使用过的,讲selected[x]赋值。就要把selected[x]嵌套在for循环中,那么为什么dfs也要嵌套在里面呢?
我们不妨一步一步分析:

没看到这个图的时候有人会问,上面那个题都是先“选”、再“不选”,调用了两次dfs,为什么这里就一次?其实这里的关键就在这个for循环,每循环并且找到一个合适的数,都会向下调用一次dfs。这里我来简单说一下:
1)首先会一直调用选完 1 2 3。
2)然后调用dfs(4),发现4>3则打印返回,注意返回到x=3的主体。
3)此时执行selected[x] = 0; available[i] = false;将x=3(第三层)的已经选的selected[x]清零,并且,将选过的3置为false(表示可选)。注意此时的i值为3。应该跳出for循环了(第三层的for循环),此时为1 2 __
4)然后返回到第二层(x=2),执行selected[x] = 0; available[i] = false;此时为1 __ __ 。此时i=2。
5)i自增后为3(这里还是第二层,x==2)。然后再执行selected[x] = i;available[i] = true;dfs(x + 1);selected[x] =0; available[i] = false;此时选的3,即 1 3 __。然后再调用dfs(x+1)
6)这里i又从1开始到3,选了1 3 2。依次类推。
问题三:(组合)
排列与组合是常用的数学方法,其中组合就是从 n 个元素中抽出 r 个元素(不分顺序且r≤n),我们可以简单地将 𝑛个元素理解为自然数 1,2,…,n,从中任取 𝑟个数。
例如 𝑛=5,r=3,所有组合为:
123,124,125,134,135,145,234,235,245,345。
注意:所有的组合,每一个组合占一行且其中的元素按由小到大的顺序排列
这里可以看出是题目二的一个改进。
同样的,我们来画一个求解图:

注意,当选择 1 5 __时,后面已经不可能再有解了,所以要剪枝,去掉这个解。
下面来看代码:
C++
#include<bits/stdc++.h>
#define N 22
using namespace std;
int n,r;
int arr[N];
void dfs(int x)
{
if(x>r)
{
for(int j=1;j<=r;j++)
{
cout<<setw(3)<<arr[j];
}
cout<<endl;
return ;
}
for(int i = arr[x-1]+1;i<=n;i++)
{
arr[x] = i;
dfs(x+1);
arr[x] = 0;
}
}
int main()
{
cin>>n>>r;
dfs(1);
return 0;
}相信这里有很多人不明白第二个for循环的逻辑。这里我们这样思考:
首先选择第一个位置的数,选完了之后要选第二个位置的数,但是要注意到第二个数一定要大于第一个数,那么就从第一个数+1开始选择。接着回溯时,会自动选下一个。
同样java版
package DFS;
import java.util.Scanner;
public class n_rarrange {
static int[] arr = new int[22];
static int n, r;
public static void dfs(int x) {
if (x > r) {
for (int j = 1; j <= r; j++) {
System.out.print(arr[j] + " ");
}
System.out.println();
return;
}
for (int i = arr[x - 1] + 1; i <= n; i++) {
arr[x] = i;
dfs(x + 1);
arr[x] = 0;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
r = sc.nextInt();
dfs(1);
}
}题目四:(组合变)
已知 n 个整数 x1,x2,⋯,xn,以及 1 个整数 k(k<n)。从 n 个整数中任选 k 个整数相加,可分别得到一系列的和。例如当 n=4,k=3,4 个整数分别为3,7,12,19 时,可得全部的组合与它们的和为:
3+7+12=22
3+7+19=29
7+12+19=38
3+12+19=34
现在,要求你计算出和为素数共有多少种。
例如上例,只有一种的和为素数:3+7+19=29
#include<bits/stdc++.h>
#define N 22
using namespace std;
int n,k;
int res[N];
int arr[N];
int counter = 0;
bool isprime(int num)
{
if (num <= 1) return false;
if (num == 2) return true;
if (num % 2 == 0) return false;
for (int i = 3; i * i <= num; i += 2) {
if (num % i == 0) {
return false;
}
}
return true;
}
void dfs(int x,int start)
{
if(x>k)
{
int summ = 0;
for(int j= 1;j<=k;j++)
{
summ += res[j];
}
if(isprime(summ))
{
counter++;
}
return ;
}
for(int i = start; i<=n; i++)
{
res[x] = arr[i];
dfs(x+1,i+1);
res[x] = 0;
}
}
int main()
{
cin>>n>>k;
for(int i= 1; i<=n ;i++) cin>>arr[i];
dfs(1,1);
cout<<counter<<endl;
return 0;
}五:搜索迷宫准备条件
经常会遇到迷宫类问题,比如1是墙、0是路,如下:
1 1 1 1 1 1 1
1 0 0 0 0 1 1
1 0 0 0 1 0 1
1 1 1 0 1 0 1
1 0 0 0 0 0 1
1 1 1 1 0 1 1
1 0 0 0 0 0 1
1 1 1 1 1 1 1
我们现在有几个问题要解决:
1)用什么来存储迷宫?2)如何控制向上、下、左、右移动?
3)如何判断这个位置能不能走(遇到1不能走,遇到0可以走)
接下来一一解决问题:
1)显然可以用二维数组来存储
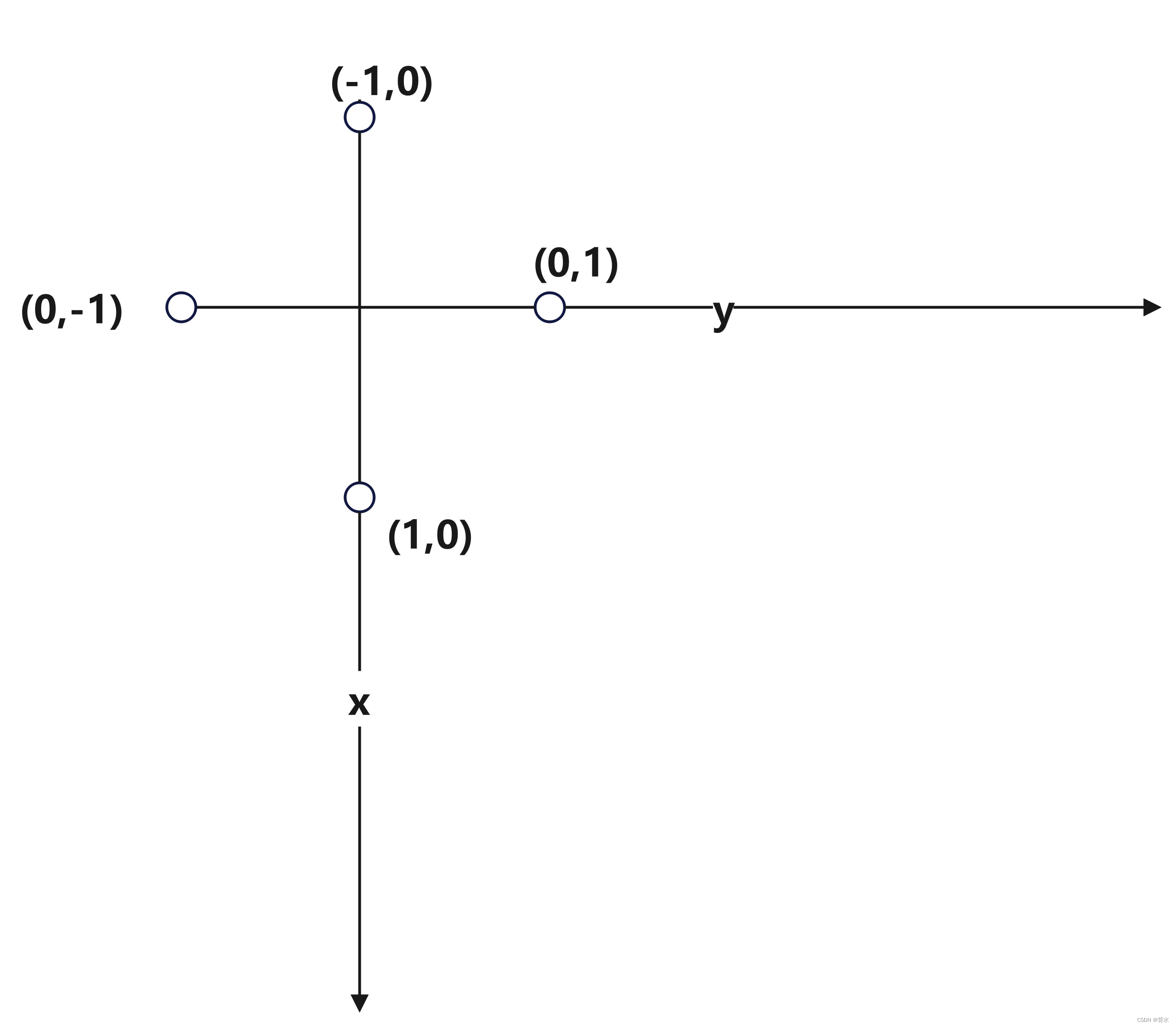
2)先看下面一个图:
我们要知道:在计算机内部的x和y轴习惯旋转90度,中点是(0,0)。如果f(x,y)表示当前位置,那么:有
f(x+1,y) 向下走 f(x,y+1) 向右走 f(x-1,y) 向上走 f(x,y-1) 向左走 但是如果有8个方向供选择呢?这将会很麻烦。这将会很麻烦。所有引出方向向量dx、dy。有下面定义:
int dx[] = {-1 , 0 , 1 , 0}; int dy[] = {0 , 1 , 0 , -1};这样通过下面代码:
for(int i=0;i<4;i++) { int a = x + dx[i]; int b = y + dy[i]; if(a <0 || a>=h || b<0||b>=w) continue; if(g[a][b] != 0) continue; f(a,b); }这样就按照逆时针,上、右、下、左的顺序遍历当前所在位置的四周。
六洛谷P1596
由于近期的降雨,雨水汇集在农民约翰的田地不同的地方。我们用一个 𝑁×𝑀(1≤𝑁≤100,1≤𝑀≤100)N×M(1≤N≤100,1≤M≤100) 的网格图表示。每个网格中有水(W) 或是旱地(.)。一个网格与其周围的八个网格相连,而一组相连的网格视为一个水坑。约翰想弄清楚他的田地已经形成了多少水坑。给出约翰田地的示意图,确定当中有多少水坑。
输入第 11 行:两个空格隔开的整数:N 和 M。
第 22 行到第 𝑁+1N+1 行:每行 𝑀M 个字符,每个字符是 W 或 .,它们表示网格图中的一排。字符之间没有空格。
输出一行,表示水坑的数量。
10 12 W........WW. .WWW.....WWW ....WW...WW. .........WW. .........W.. ..W......W.. .W.W.....WW. W.W.W.....W. .W.W......W. ..W.......W.
输出:
3
刚开始有点不理解每次dfs的时是对一片区域进行遍历。那么要如何算出一共有的区域数呢?但是仔细想一下,发现一旦一个区域遍历完了,他就跳出dfs这个函数了,我直接在主函数调用dfs后面加一个res++,不就好了吗?
这里总结一下,通过dfs遍历连通的区域,注意不连通的区域是独立的(也就是说不连通的区域,其中有一个遍历完了不会影响其他区域)。注意这里的dfs是一个工具(一个可以找到相连通的区域,并在上面操作的工具,一旦遍历到了这个地方,就可以给这个地方标记。)
#include<bits/stdc++.h>
using namespace std;
const int N =110;
char g[N][N];
int res =0;
bool st[N][N];
int n,m;
int dx[]={-1,-1,0,1,1,1,0,-1};
int dy[]={0,1,1,1,0,-1,-1,-1};
void dfs(int x,int y)
{
for(int i=0;i<8;i++)
{
int a = x+dx[i];
int b = y+dy[i];
if(a<0 || a>=n || b<0 || b>=m) continue;
if(g[a][b] != 'W') continue;
if(st[a][b]) continue;
st[a][b] = true;
dfs(a,b);
}
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
{
cin>>g[i];
}
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
if(g[i][j]=='W' && !st[i][j])
{
dfs(i,j);
res++;
}
}
}
cout<<res;
return 0;
}六
给你一个n*n的棋盘,每个地方都能下棋,但是要保证每行每列只下一个棋,共下n个棋,求可以放的方案数。
#include<iostream>
#include<string>
using namespace std;
const int N = 21;
int arr[N][N];
bool isok[N];
int n,res=0;
void dfs(int x)
{
if(x>=n)
{
res++;
return;
}
for(int i=0;i<n;i++)
{
if(!isok[i])
{
arr[x][i]=1;
isok[i]=true;
dfs(x+1);
arr[x][i]=0;
isok[i]=false;
}
}
}
int main()
{
cin>>n;
dfs(0);//一定要注意,棋盘第一行的索引从0开始,所以dfs从第0行开始。
cout<<res;
return 0;
}七:
在一个给定形状的棋盘(形状可能是不规则的)上面摆放棋子,棋子没有区别。
要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列,请编程求解对于给定形状和大小的棋盘,摆放 k𝑘 个棋子的所有可行的摆放方案数目 C𝐶。
输入格式
输入含有多组测试数据。
每组数据的第一行是两个正整数 𝑛,𝑘,用一个空格隔开,表示了将在一个 𝑛∗𝑛 的矩阵内描述棋盘,以及摆放棋子的数目。当为-1 -1时表示输入结束。
随后的 n𝑛 行描述了棋盘的形状:每行有 𝑛 个字符,其中 # 表示棋盘区域, . 表示空白区域(数据保证不出现多余的空白行或者空白列)。
输出格式
对于每一组数据,给出一行输出,输出摆放的方案数目 C
#include<iostream>
#include<string>
using namespace std;
const int N = 21;
char arr[N][N];
bool isok[N];
int n,k,res;
void dfs(int x,int place)
{
if(place==k)
{
res++;
return ;
}
if(x>=n)
{
return ;
}
for(int i=0;i<n;i++) //放棋子的情况
{
if(!isok[i] && arr[x][i]=='#')
{
isok[i] = true;
dfs(x+1,place+1);
isok[i] = false;
}
}
dfs(x+1,place);//不放的情况
}
int main()
{
while(cin>>n>>k,n>0 && k>0)
{
for(int i=0;i<n;i++)
{
cin>>arr[i];
}
res = 0;
dfs(0,0);
cout<<res<<endl;
}
return 0;
}当时往来有某一行/多行不选的情况。
下面是用一个参数的代码(copy别人的)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
const int N = 10; // n 最大是 8,多开到 10
int n, k; // n * n 棋盘,要放 k 个棋子
char g[N][N]; // 存地图
int res; // 存答案
bool row[N]; // bool 数组存每一行是否放过棋子
int cnt; // 存目前放了多少个棋子
void dfs(int x)
{
if (cnt == k) // 如果已经放完 k 个棋子
{
res ++ ; // 答案加一
return; // 不用在执行下面的操作,直接 return
}
if (x > n) return; // 判断边界,如果超出棋盘范围,则之前的搜索方案不合法,直接 return
for (int i = 1; i <= n; i ++ ) // 枚举棋子放在第几行
{
if (g[i][x] == '#' && !row[i]) // 如果该位置属于棋盘范围且这行之前没有放过棋子
{
cnt ++ ; // 多放了一个,cnt 加一
row[i] = true; // 标记这一行,之后不能放
dfs(x + 1); // dfs 下一列
cnt -- ; // 回溯,拿掉这颗棋
row[i] = false; // 回溯,这一行又能放了
}
}
dfs(x + 1); // 还要在进行 dfs 是因为 k <= n,有可能不是每列都放了棋子,这里的 dfs 搜索这一列不放棋子的情况
}
int main()
{
while (scanf("%d%d", &n, &k)) // 多组数据
{
if (n == -1 && k == -1) break; // 输入结束,跳出循环
for (int i = 1; i <= n; i ++ )
{
getchar(); // 因为 scanf 输入会读到换行,所以要用 getchar 先把换行读完
for (int j = 1; j <= n; j ++ ) scanf("%c", &g[i][j]); // 输入地图不多说
}
res = cnt = 0; // 初始化
memset(row, 0, sizeof row); // 初始化
dfs(1); // 执行 dfs
printf("%d\n", res); // 输出答案不多说
}
return 0;
}
作者:种花家的兔兔
链接:https://www.acwing.com/solution/content/133704/只用一个变量要注意的是,每次选完棋、回溯的时候要记得将棋数减一。