【代码随想录】【算法训练营】【第43天】 [518]零钱兑换II [377]组合总和IV [卡码57]爬楼梯

news2024/11/17 11:40:51

前言

思路及算法思维，指路代码随想录。
题目来自 LeetCode。
部分题目来自卡码网。

day 43，极其困难的周三~

题目详情

[518] 零钱兑换II

题目描述

518 零钱兑换II

解题思路

前提：假设每一种面额的硬币有无限个，求组合数
思路：完全背包问题，求组合数，dp[i][j]: 在[0, i]中取硬币凑成总金额为j的组合数，dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]，使用一维数组即为dp[j] = dp[j] + dp[j-coins[i]]。
重点：组合数的遍历顺序：先遍历物品，后遍历背包。

代码实现

C语言

dp[i][j]

// 完全背包问题, 求组合数
// dp[i][j]: 在[0, i]中取硬币凑成总金额为j的组合数
// dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]

int change(int amount, int* coins, int coinsSize) {
    int dp[coinsSize][amount + 1];
    // dp数组初始化
    dp[0][0] = 1;
    for (int j = 1; j <= amount; j++) {
        if (j < coins[0]) {
            dp[0][j] = 0;
        } else {
            dp[0][j] = dp[0][j - coins[0]];
        }
    }
    // 组合数：先遍历硬币，再遍历总金额
    for (int i = 1; i < coinsSize; i++) {
        for (int j = 0; j <= amount; j++) {
            dp[i][j] = dp[i - 1][j];
            if (j >= coins[i]) {
                dp[i][j] += dp[i][j - coins[i]];
            }
        }
    }
    return dp[coinsSize - 1][amount];
}

dp[j]

// 完全背包问题, 求组合数
// 压缩dp[i][j]为dp[j]: 在[0, i]中取硬币凑成总金额为j的组合数
// dp[j] = dp[j] + dp[j-coins[i]]

int change(int amount, int* coins, int coinsSize) {
    int dp[amount + 1];
    // dp数组初始化
    dp[0] = 1;
    for (int j = 1; j <= amount; j++) {
        dp[j] = 0;
    }
    // 组合数：先遍历硬币，再遍历总金额
    for (int i = 0; i < coinsSize; i++) {
        for (int j = coins[i]; j <= amount; j++) {
            if (j >= coins[i]) {
                dp[j] += dp[j - coins[i]];
            }
        }
    }
    return dp[amount];
}

[377] 组合总和IV

题目描述

377 组合总和IV

解题思路

前提：数组元素不同，顺序不同的序列被视作不同的组合。
思路：完全背包问题，求排列数，dp[i][j]: 从数组nums的前i个位置中取元素，和为j的组合数，dp[i][j] = dp[i-1][j] + dp[numsSize][j-nums[i]]；压缩一维数组为dp[j] = dp[j] + dp[j-nums[i]]
重点：遍历顺序，二维数组的推导公式，以及初始化； dp[numsSize][j - nums[i]]可以理解为最后一位为nums[i]的排列数。

代码实现

C语言

dp[i][j]

dp[i][j]: 从数组nums的前i个位置中取元素，和为j的组合数，所以dp数组大小为int dp[numsSize + 1][target + 1]，返回为dp[numsSize][target]，dp[i][j] = dp[i-1][j] + dp[numsSize][j-nums[i]]

// 完全背包, 排列个数
// dp[i][j]: 从数组nums的前i个位置中取元素，和为j的组合数
// dp[i][j] = dp[i-1][j] + dp[numsSize][j-nums[i]]

int combinationSum4(int* nums, int numsSize, int target) {
    int dp[numsSize + 1][target + 1];
    // dp数组初始化
    for (int i = 0; i <= numsSize; i++) {
        // 首列
        dp[i][0] = 1;
    }
    for (int j = 1; j <= target; j++) {
        // 首行
        dp[0][j] = 0;
    }
    // 遍历, 排列数, 先遍历目标和target, 后遍历数组nums
    for (int j = 0; j <= target; j++) {
        for (int i = 1; i <= numsSize; i++) {
            dp[i][j] = dp[i - 1][j];
            if ((j >= nums[i - 1]) && (dp[i - 1][j] < INT_MAX - dp[numsSize][j - nums[i - 1]])) {
                dp[i][j] += dp[numsSize][j - nums[i - 1]];
            }
        }
    }
    return dp[numsSize][target];
}

dp[i][j]: 从数组nums的前i中取元素，和为j的组合数，所以dp数组大小为int dp[numsSize][target + 1]，返回为dp[numsSize - 1][target]，
dp[i][j] = dp[i-1][j] + dp[numsSize - 1][j-nums[i]]

// 完全背包, 排列个数
// dp[i][j]: 从数组nums的前i中取元素，和为j的组合数
// dp[i][j] = dp[i-1][j] + dp[numsSize - 1][j-nums[i]]
// dp[numsSize - 1][j - nums[i]]可以理解为最后一位为nums[i]的排列数

int combinationSum4(int* nums, int numsSize, int target) {
    int dp[numsSize][target + 1];
    // dp数组初始化
    dp[0][0] = 1;
    for (int i = 0; i < numsSize; i++) {
        dp[i][0] = 1;
    }
    // 遍历, 排列数, 先遍历目标和target, 后遍历数组nums
    for (int j = 1; j <= target; j++) {
        for (int i = 0; i < numsSize; i++) {
            if (i == 0) {
                dp[i][j] = 0;
            } else {
                dp[i][j] = dp[i - 1][j];
            }
            if ((j >= nums[i]) && (dp[i][j] < INT_MAX - dp[numsSize - 1][j - nums[i]])) {
                dp[i][j] += dp[numsSize - 1][j - nums[i]];
            }
        }
    }
    return dp[numsSize - 1][target];
}

dp[j]

// 完全背包, 排列个数
// dp[j]: 从数组nums的前i中取元素，和为j的排列数
// dp[j] = dp[j] + dp[j-nums[i]]

int combinationSum4(int* nums, int numsSize, int target) {
    int dp[target + 1];
    // dp数组初始化
    dp[0] = 1;
    for (int j = 1; j <= target; j++) {
        dp[j] = 0;
    }
    // 遍历, 排列数, 先遍历目标和target, 后遍历数组nums
    for (int j = 0; j <= target; j++) {
        for (int i = 0; i < numsSize; i++) {
            if ((j >= nums[i]) && (dp[j] < INT_MAX - dp[j - nums[i]])) {
                dp[j] += dp[j - nums[i]];
            }
        }
    }
    return dp[target];
}

[卡码57] 爬楼梯

题目描述

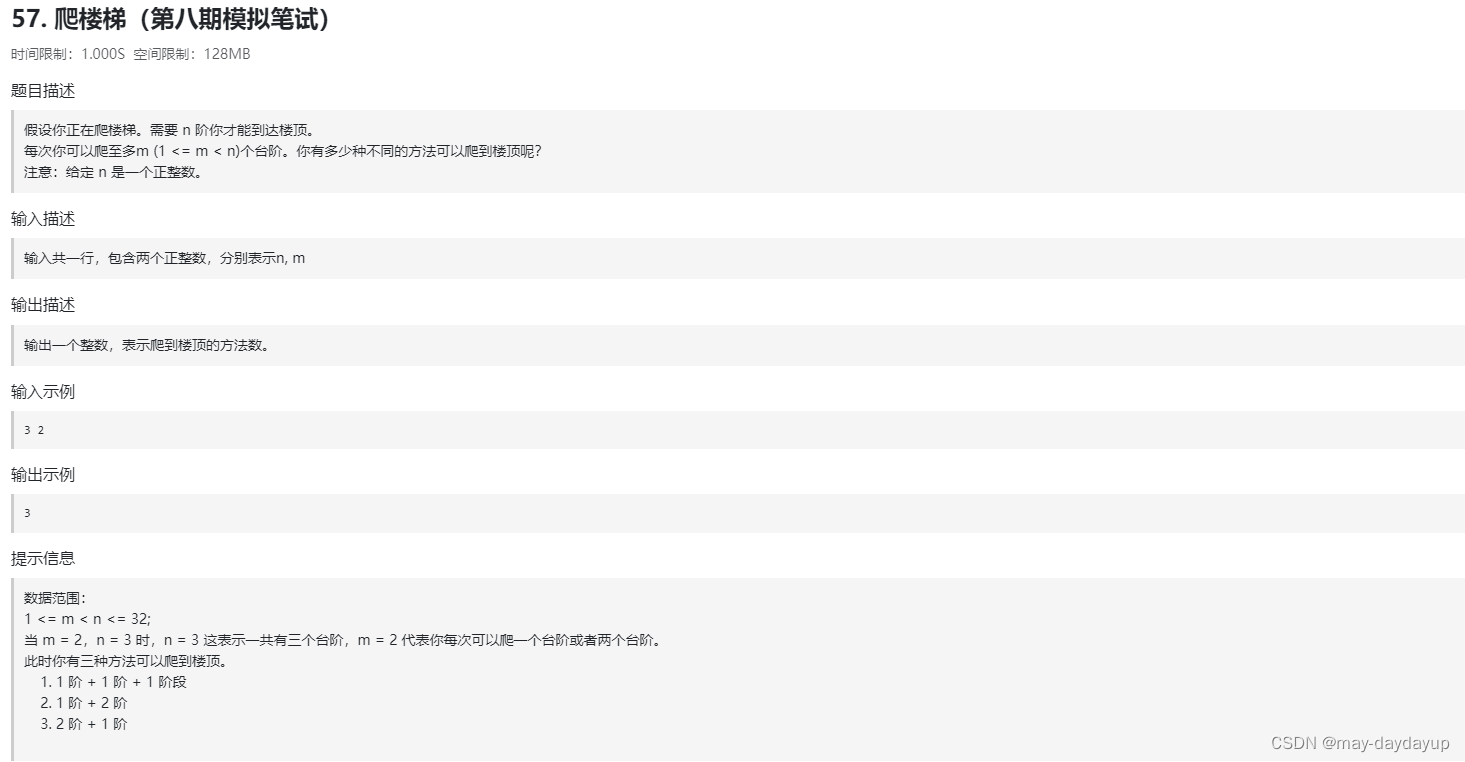
卡码57 爬楼梯

解题思路

前提：求到达楼顶的不同方法的数量
思路：完全背包，求排列数，dp[i][j]: 至多每次i个台阶，可以到达j阶高度的排列方法数, dp[i][j] = dp[i-1][j] + dp[m][j-i]；压缩一维数组为dp[[j] = dp[j] + dp[j-i]
重点：遍历顺序，二维数组的推导公式，以及初始化。

代码实现

C语言

dp[i][j]

#include <stdio.h>
#include <stdlib.h>
 
// 完全背包，求排列数
// dp[i][j]: 至多每次i个台阶，可以到达j阶高度的排列方法数
// dp[i][j] = dp[i-1][j] + dp[m][j-i]
 
int clamb(int n, int m)
{
    int dp[m + 1][n + 1];
    // 初始化dp数组
    for (int i = 0; i <= m; i++) {
        // 首行
        dp[i][0] = 1;
    }
    for (int j = 1; j <= n; j++) {
        // 首列
        dp[0][j] = 0;
    }
    // 排列数，先遍历高度，再遍历每次台阶数
    for (int j = 1; j <= n; j++) {
        for (int i = 1; i <= m; i++) {
            dp[i][j] = dp[i - 1][j];
            if (j >= i) {
                dp[i][j] += dp[m][j - i];
            }
            //printf("%d %d %d\n", i, j, dp[i][j]);
        }
    }
    return dp[m][n];
}
 
int main()
{
    int n;
    int m;
    scanf("%d %d",&n, &m);
    int ans = clamb(n, m);
    printf("%d", ans);
    return 0;
}

dp[j]

#include <stdio.h>
#include <stdlib.h>
 
// 完全背包，求排列数
// dp[j]: 至多每次i个台阶，可以到达j阶高度的排列方法数
// dp[[j] = dp[j] + dp[j-i]
 
int clamb(int n, int m)
{
    int dp[n + 1];
    // 初始化dp数组
    dp[0] = 1;
    for (int j = 1; j <= n; j++) {
        dp[j] = 0;
    }
    // 排列数，先遍历高度，再遍历每次台阶数
    for (int j = 1; j <= n; j++) {
        for (int i = 1; i <= m; i++) {
            if (j >= i) {
                dp[j] += dp[j - i];
            }
            //printf("%d %d %d\n", i, j, dp[j]);
        }
    }
    return dp[n];
}
 
int main()
{
    int n;
    int m;
    scanf("%d %d",&n, &m);
    int ans = clamb(n, m);
    printf("%d", ans);
    return 0;
}

今日收获

完全背包问题：组合数（先遍历物品，后遍历背包），排列数（先遍历背包，后遍历物品）；虽然一维dp数组的递推公式都是一样的，但是二维dp数组的递推公式有较大的差别，初始化也不太一样，排列数的 dp[i][j] = dp[i-1][j] + dp[numsSize - 1][j-nums[i]] 明显更难以理解一些。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1839211.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！