题目来源

415. 字符串相加 - 力扣（LeetCode）

题目描述

给定两个字符串形式的非负整数 num1 和 num2 ，计算它们的和并同样以字符串形式返回。

你不能使用任何內建的用于处理大整数的库（比如 BigInteger）， 也不能直接将输入的字符串转换为整数形式。

示例

示例 1：

输入：num1 = "11", num2 = "123"
输出："134"

示例 2：

输入：num1 = "456", num2 = "77"
输出："533"

示例 3：

输入：num1 = "0", num2 = "0"
输出："0"

提示

• 1 <= num1.length, num2.length <= 10^4
• num1 和 num2 都只包含数字 0-9
• num1 和 num2 都不包含任何前导零

题目解析

本题需要我们模拟整数加法运算。

两个整数的加法运算，都是从个位对齐，逐位相加。

本题给定的是数字字符串，因此整数的个位，其实就数字字符串的尾巴（索引位s.length-1）

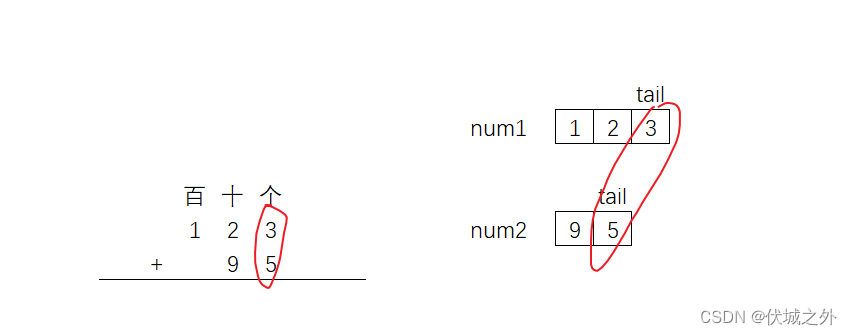
因此，我们可以定义两个指针 i，j ，分别指向num1和num2的尾巴索引位置，即初始时：

• i = num1.length - 1
• j = num2.length - 1

然后我们将 num1[i] 和 num2[j] 相加，进行个位部分相加

此时个位相加的结果没有超过10，即无需进位，因此我们 i--, j-- 向前移动一位，进行十位部分相加

此时十位部分，num1[i] + num2[j] 的结果result为 11，超过了10，即需进位1（result % 10），当前十位结果为1（result / 10）

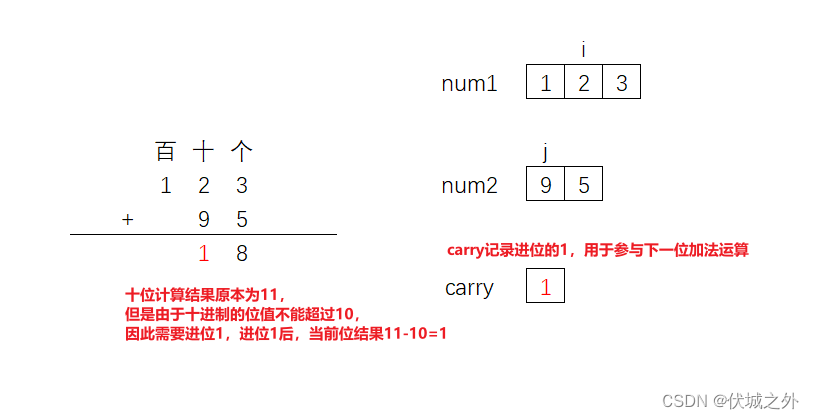
之后，i--，j--继续向前移动，此时发现，j指针越界了

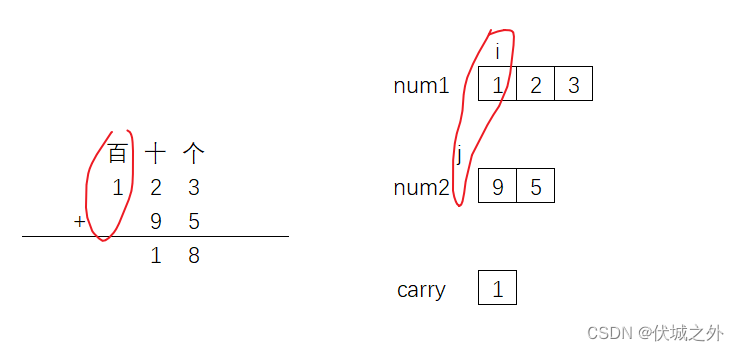
但是百位任然需要进行计算，因为num1的百位还有值，且进位carry也有值，因此此轮我们需要将

num1的百位和carry进行相加

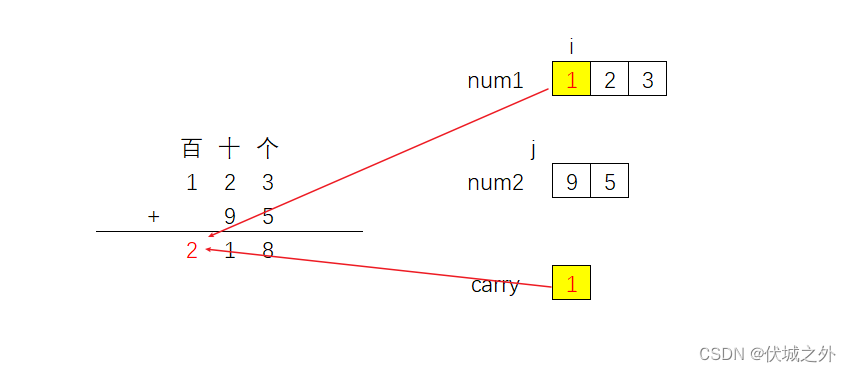
相加后，进位值被消耗，carry应该重新变为0，然后百位加法完成。

之后继续 i--，j--，向前移动到下一位，此时 i，j都越界了，且carry==0，则可以认为计算完毕

---

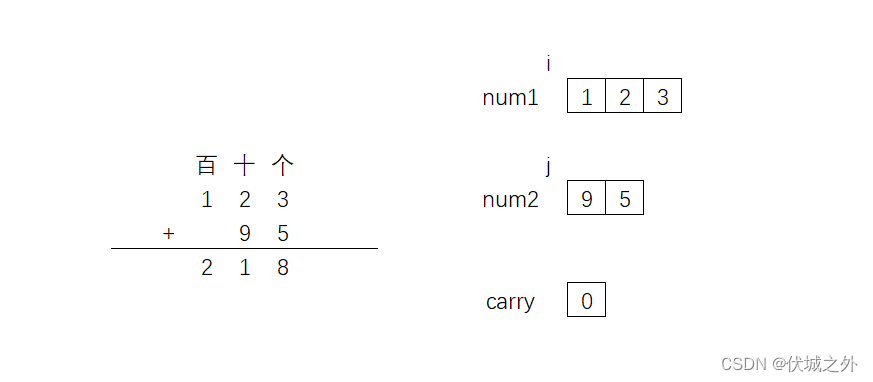
因此，模拟整数加法运算其实很简单，主要逻辑为：

• 对齐两个整数字符串的十进制位（个位对个位，十位对十位...），即字符串尾部对齐
• 对应位相加，如果结果result超过10，则需要进位 result % 10，进位后，本位结果为 result / 10
• 实际上对应位相加，不仅是num1[i]和num2[j]的相加，还要加上上一轮的进位值carry
• 只要num1或num2没有遍历完（还有剩余位未参加计算），或者上一轮计算的进位carry不为0，则我们要继续相加

Java算法源码

class Solution {
    public String addStrings(String a, String b) {
        // 个位（字符串尾部）对齐, 即a[i]是a的个位值，b[j]是b的个位值
        int i = a.length() - 1;
        int j = b.length() - 1;
        // 记录进位值
        int carry = 0;

        // 记录结果串
        StringBuilder sb = new StringBuilder();

        // 只要a未遍历完，或b未遍历完，或上一轮进位carry不为0，则需要继续加法
        while (i >= 0 || j >= 0 || carry != 0) {
            // a[i]位的数x
            int x = i >= 0 ? a.charAt(i) - '0' : 0;
            // b[j]位的数y
            int y = j >= 0 ? b.charAt(j) - '0' : 0;

            // 当前位相加结果
            int result = x + y + carry;

            // 当前位计算结果不能超过10（十进制的位值不能超过10）
            sb.append(result % 10);
            // 超过10需要进位
            carry = result / 10;

            // 向前移动到下一位
            i--;
            j--;
        }

        // 由于sb是依次录入个位、十位、百位...的结果值，因此sb实际是倒的数字，我们需要反转一下
        return sb.reverse().toString();
    }
}

 

JS算法源码

var addStrings = function (a, b) {
  // 个位（字符串尾部）对齐, 即a[i]是a的个位值，b[j]是b的个位值
  let i = a.length - 1;
  let j = b.length - 1;
  // 记录进位值
  let carry = 0;

  // 记录结果串
  const ans = [];

  // 只要a未遍历完，或b未遍历完，或上一轮进位carry不为0，则需要继续加法
  while (i >= 0 || j >= 0 || carry != 0) {
    // a[i]位的数x
    const x = i >= 0 ? parseInt(a[i]) : 0;
    // b[j]位的数y
    const y = j >= 0 ? parseInt(b[j]) : 0;

    // 当前位相加结果
    const result = x + y + carry;

    // 当前位计算结果不能超过10（十进制的位值不能超过10）
    ans.push(result % 10);
    // 超过10需要进位
    carry = parseInt(result / 10);

    // 向前移动到下一位
    i--;
    j--;
  }

  // 由于ans是依次录入个位、十位、百位...的结果值，因此ans实际是倒的数字，我们需要反转一下
  return ans.reverse().join("");
};

 

Python算法源码

class Solution(object):
    def addStrings(self, a, b):
        # 个位（字符串尾部）对齐, 即a[i]是a的个位值，b[j]是b的个位值
        i = len(a) - 1
        j = len(b) - 1
        # 记录进位值
        carry = 0

        # 记录结果串
        ans = []

        # 只要a未遍历完，或b未遍历完，或上一轮进位carry不为0，则需要继续加法
        while i >= 0 or j >= 0 or carry != 0:
            # a[i]位的数x
            x = int(a[i]) if i >= 0 else 0
            # b[j]位的数y
            y = int(b[j]) if j >= 0 else 0

            # 当前位相加结果
            result = x + y + carry

            # 当前位计算结果不能超过10（十进制的位值不能超过10）
            ans.append(result % 10)
            # 超过10需要进位
            carry = result // 10

            # 向前移动到下一位
            i -= 1
            j -= 1

        # 由于ans是依次录入个位、十位、百位...的结果值，因此ans实际是倒的数字，我们需要反转一下
        ans.reverse()
        return "".join(map(str, ans))

C算法源码

char *addStrings(char *a, char *b) {
    // 个位（字符串尾部）对齐, 即a[i]是a的个位值，b[j]是b的个位值
    int i = strlen(a) - 1;
    int j = strlen(b) - 1;
    // 记录进位值
    int carry = 0;

    // 记录结果串
    char *sb = (char *) calloc((int) fmax(i, j) + 3, sizeof(char));
    int sb_size = 0;

    // 只要a未遍历完，或b未遍历完，或上一轮进位carry不为0，则需要继续加法
    while (i >= 0 || j >= 0 || carry != 0) {
        // a[i]位的数x
        int x = i >= 0 ? a[i] - '0' : 0;
        // b[j]位的数y
        int y = j >= 0 ? b[j] - '0' : 0;

        // 当前位相加结果
        int result = x + y + carry;

        // 当前位计算结果不能超过10（十进制的位值不能超过10）
        sb[sb_size++] = (char) ((result % 10) + '0');
        // 超过10需要进位
        carry = result / 10;

        // 向前移动到下一位
        i--;
        j--;
    }

    // 由于sb是依次录入个位、十位、百位...的结果值，因此sb实际是倒的数字，我们需要反转一下
    int l = 0;
    int r = sb_size - 1;

    while (l < r) {
        char tmp = sb[l];
        sb[l] = sb[r];
        sb[r] = tmp;
        l++;
        r--;
    }

    return sb;
}

C++算法源码

class Solution {
public:
    string addStrings(string a, string b) {
        // 个位（字符串尾部）对齐, 即a[i]是a的个位值，b[j]是b的个位值
        int i = a.length() - 1;
        int j = b.length() - 1;
        // 记录进位值
        int carry = 0;

        // 记录结果串
        string sb;

        // 只要a未遍历完，或b未遍历完，或上一轮进位carry不为0，则需要继续加法
        while (i >= 0 || j >= 0 || carry != 0) {
            // a[i]位的数x
            int x = i >= 0 ? a[i] - '0' : 0;
            // b[j]位的数y
            int y = j >= 0 ? b[j] - '0' : 0;

            // 当前位相加结果
            int result = x + y + carry;

            // 当前位计算结果不能超过10（十进制的位值不能超过10）
            sb += to_string(result % 10);
            // 超过10需要进位
            carry = result / 10;

            // 向前移动到下一位
            i--;
            j--;
        }

        // 由于sb是依次录入个位、十位、百位...的结果值，因此sb实际是倒的数字，我们需要反转一下
        reverse(sb.begin(), sb.end());

        return sb;
    }
};