题干:
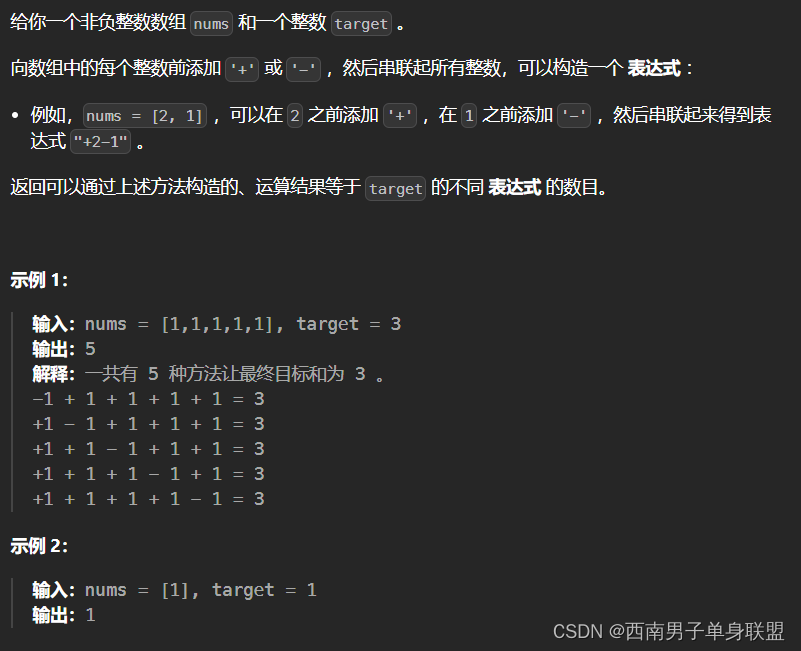
代码:
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for(int i : nums) sum += i;
if(abs(target) > sum)return 0;
if((sum + target) % 2 != 0)return 0;
int bagweight = (sum + target) / 2;
vector<int>dp(bagweight + 1, 0);
dp[0] = 1;
for(int i = 0; i < nums.size(); i++){
for(int j = bagweight; j >= nums[i]; j--){
dp[j] += dp[j - nums[i]];
}
}
return dp[bagweight];
}
};思路:把带加号的数归为甲类,带减号的归为乙类,可得方程组:
甲 + 乙 = sum ①
甲 - 乙 = target ②
(① + ②) / 2 可得甲 = (sum + target) / 2,问题转化为了将容量为甲的背包装满有多少种方法。
定义:dp[j]值代表着将容量为j的背包装满有多少种方法
递推公式:dp[j] += dp[j - nums[i]]
对递推公式的解释:
想象一下你有一个背包,可以装下一定重量的物品,现在面前有一堆物品,每个物品都有自己的重量。`dp[j]` 可以理解为:背包总重量为 `j` 时,你有多少种不同的方法装满这个背包。
现在,你面前有一个新的物品,重量是 `num`。你想知道,如果考虑这个新物品,背包总重量为 `j` 的装满方式增加多少种。
这时候,`dp[j-num]` 就变得很重要了。它表示:如果你不包括这个新物品,而是用之前的物品装满一个总重量为 `j-num` 的背包,你有多少种方法。
那么,`dp[j] += dp[j-num]` 这个操作,实际上就是在说:“如果我已经知道怎么装满一个 `j-num` 重量的背包(有 `dp[j-num]` 种方法),那么我只需要把这个新物品(重量为 `num`)加进去,就可以得到一个总重量为 `j` 的新背包了!”,感觉跟最短路径那道题有点像。
所以,每当你看到一个新的物品,你就会想:“这个物品能不能加到我之前的某个背包里呢?如果可以,那我就多了一种新的装法!”这个过程,就是通过 `dp[j] += dp[j-num]` 来实现的。
初始化:dp[0] = 1,必须初始化为1否则之后的都推不出来
之后都一样