42. 接雨水
文字讲解:代码随想录
视频讲解:单调栈,经典来袭!LeetCode:42.接雨水_哔哩哔哩_bilibili
解题思路
思路一:单调栈
我们要找到矩形作为底时,左边和右边第一个比它大的元素

1.使用单调栈内元素的顺序
应该是从栈头到栈底,是从小到大的,因为一旦发现更大的了,就出现凹槽了,栈头左边第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子
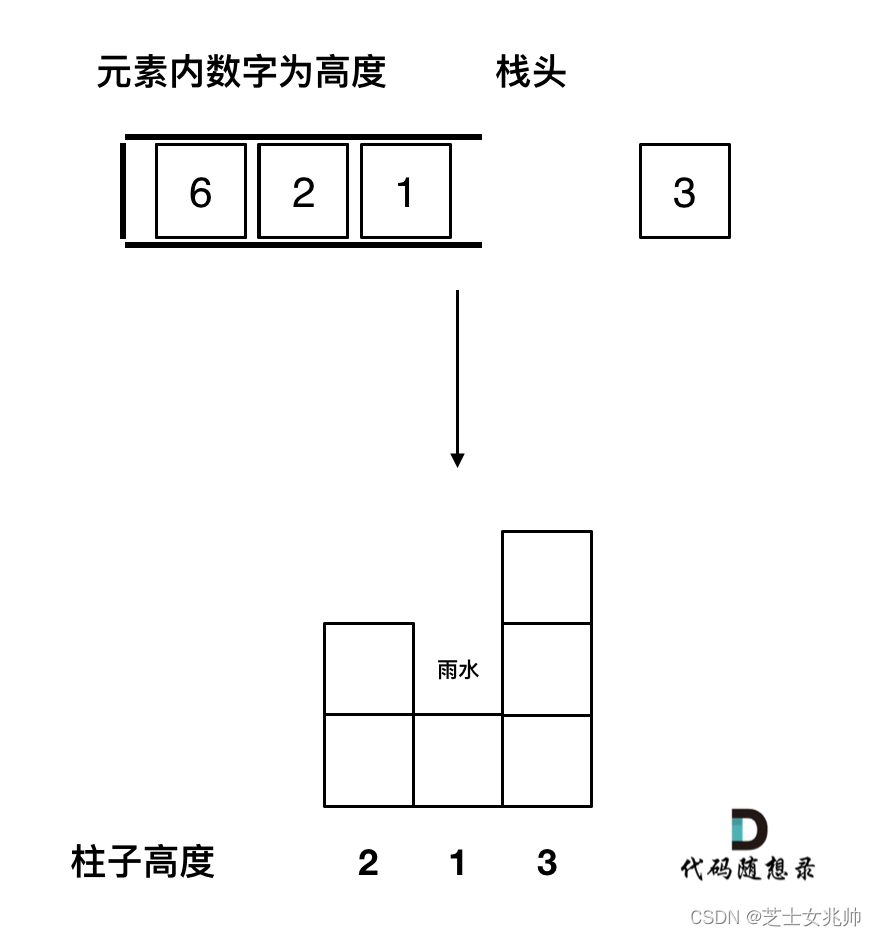
2.模拟过程
h[i] < h[st.top()] 直接加入到栈中
h[i] == h[st.top()] 弹出和直接加入都可,结果是一样的,只是计算过程不同,我们先按加入来算
h[i] > h[st.top()] 此时就发现凹槽了
mid = st.top() 先存柱子底的下标,然后弹出,才能取左边的凹槽
st.pop()
h = min(st.top(),h[i]) - h[mid] 这一行雨水的高度
w = i - st.top() - 1; 这一行雨水的宽度
s+=h*w
然后重复处理,按照我们这种计算结果,那么遇到相同的情况,计算结果就为0,不影响结果
class Solution {
public:
int trap(vector<int>& height) {
stack<int> st;
int sum = 0;
st.push(0); //第一个元素入栈
for(int i = 1 ;i < height.size(); i++)
{
if(height[i]<height[st.top()] || height[i]==height[st.top()])
st.push(i);
else
{
while(!st.empty() && height[i]>height[st.top()])
{
int mid = st.top();
st.pop();
if(!st.empty()) //因为有pop操作,还需要判断是否为空栈
{
int h = min(height[i],height[st.top()]) - height[mid];
int w = i - st.top() - 1;
sum+=h*w;
}
}
st.push(i);
}
}
return sum;
}
};84.柱状图中最大的矩形
文字讲解:代码随想录
视频讲解:单调栈,又一次经典来袭! LeetCode:84.柱状图中最大的矩形_哔哩哔哩_bilibili
解题思路
1.基础思路
假设我们遍历到6,左边和右边都比它小,无法扩展,因此面积为6*1
遍历的是5,左边是1,比它小,无法扩展,右边是6,比它大,可以扩展,面积为5*2
因此,我们只需要找左和右边第一个比它小的,这样就可以找到宽,高就是当前这个柱子
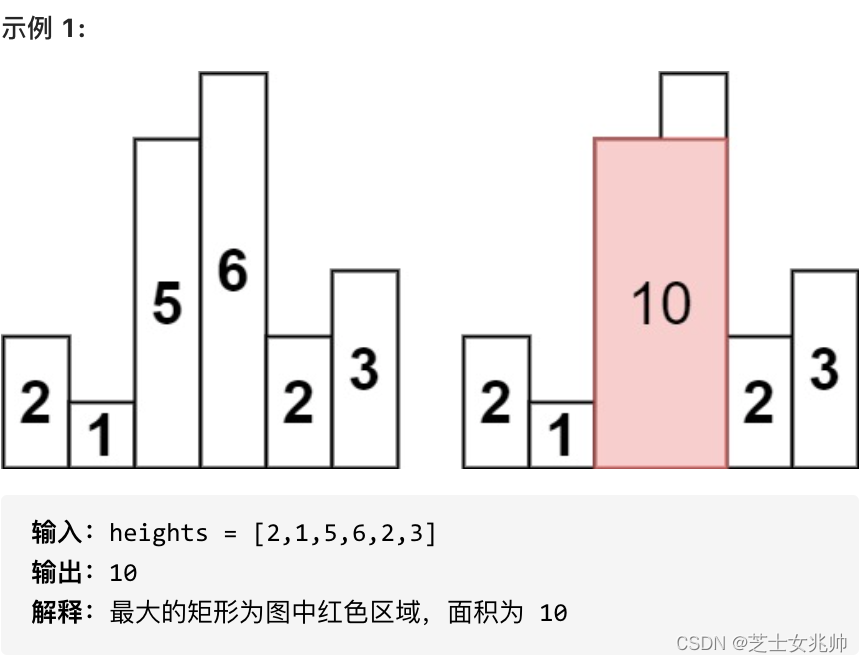
2.单调栈顺序
因为要找的是第一个比它小的,因此从栈顶到栈底是从大到小的,递减的
3.模拟过程
当遇到第一个小与栈口元素时
mid = st.top();
左边比它小的一定是遍历过的元素,也就是栈口元素旁边的元素
st.pop();
left = st.top();
right = i;
h = height[mid]
w = right - left -1 求的是中间的宽度
4.细节处理,首尾加0
如果数组本身就是升序的,例如[2,4,6,8],那么入栈之后 都是单调递减,一直都没有走 情况三 计算结果的哪一步,所以最后输出的就是0了。 如图:
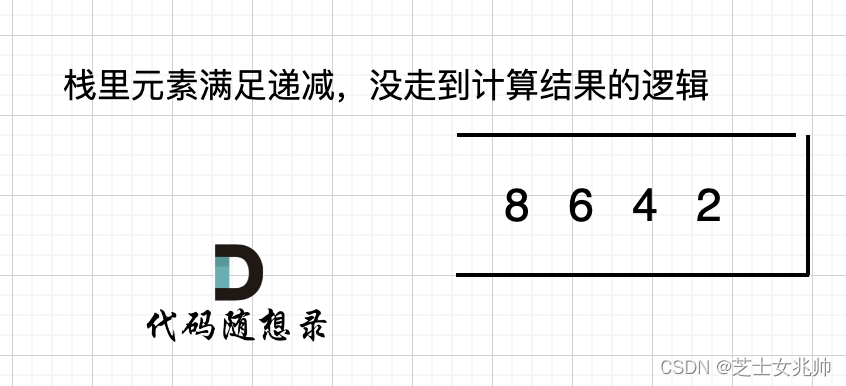
因此,尾部要加0
如果数组本身是降序的,例如 [8,6,4,2],在 8 入栈后,6 开始与8 进行比较,此时我们得到 mid(8),rigt(6),但是得不到 left,因为空栈我们不做处理,因此就跳过了
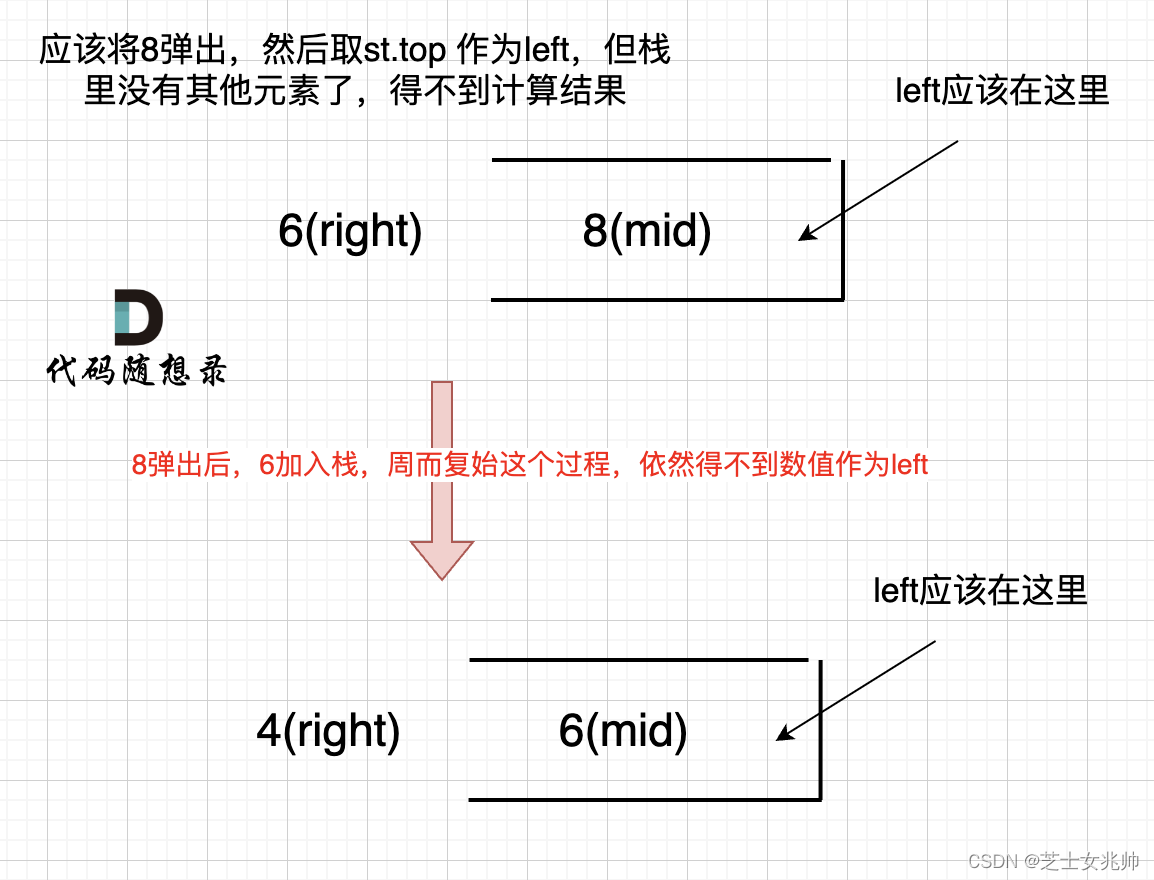
因此头部要加0
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> st; //用栈来记录遍历过的元素
heights.insert(heights.begin(),0);
heights.push_back(0);
st.push(0);
int result = 0;
for(int i = 1 ; i<heights.size();i++)
{
if(heights[i]>heights[st.top()])
st.push(i);
else if(heights[i]==heights[st.top()])
{
st.pop();
st.push(i);
}
else
{
while(!st.empty() && heights[i]< heights[st.top()])
{
int mid = st.top();
st.pop();
if(!st.empty())
{
int left = st.top();
int right = i;
int h = heights[mid];
int w = right - left - 1;
result = max(result,h*w);
}
}
st.push(i);
}
}
return result;
}
};