目录
- 回顾矩阵分解
- 交替最小二乘原理(ALS)
- 隐式反馈
- 推荐计算
- 总结
上一篇中,我们聊到了矩阵分解,在这篇文章的开始,我再为你回顾一下矩阵分解。
回顾矩阵分解
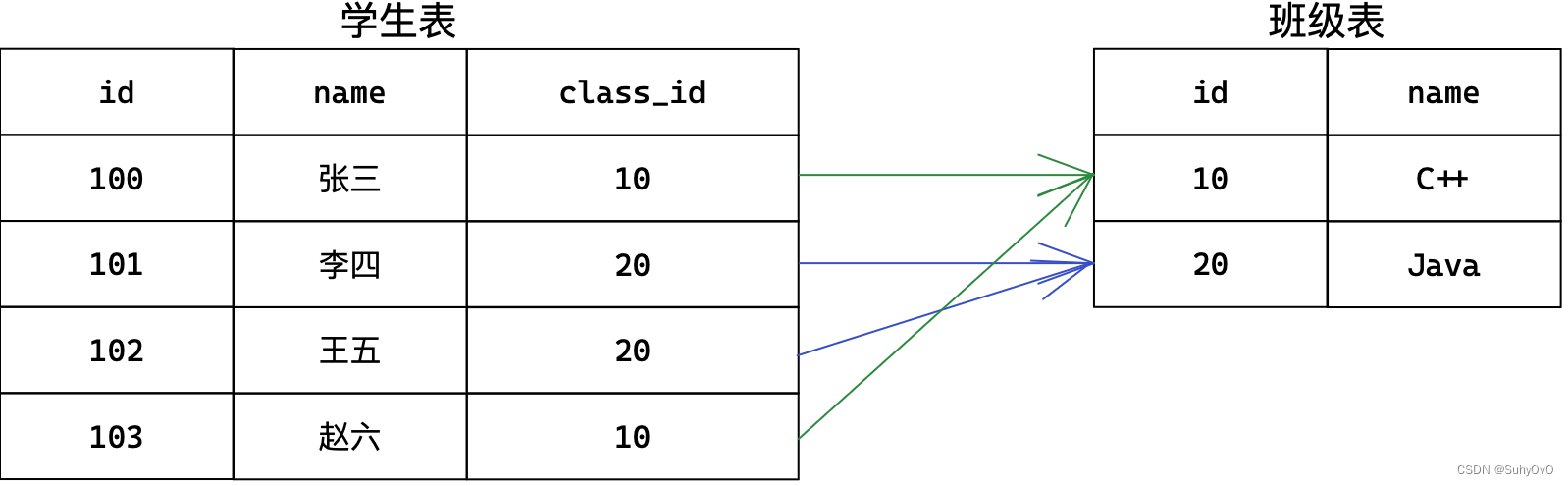
矩阵分解要将用户物品评分矩阵分解成两个小矩阵,一个矩阵是代表用户偏好的用户隐因子向量组成,另一个矩阵是代表物品语义主题的隐因子向量组成。
这两个小矩阵相乘后得到的矩阵,维度和原来的用户物品评分矩阵一模一样。比如原来矩阵维度是mn ,其中m是用户数量,n是物品数量,再假如分解后的隐因子向量是k个,那么用户隐因子向量组成的矩阵就是mk,物品隐因子向量组成的矩阵就是n*k。
得到的这两个矩阵有这么几个特点:
1.每个用户对应一个k维向量,每个物品也对应一个k维向量,就是所谓的隐因子向量;
2.两个矩阵相乘后,就得到了任何一个用户对任何一个物品的预测评分;
所以矩阵分解,所做的事就是矩阵填充。那到底怎么填充呢,换句话也就是说两个小矩阵怎么得到呢?
按照机器学习的套路,就是使用优化算法求解下面这个损失函数:
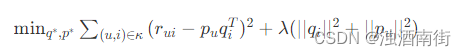
这个公式由两部分构成:加号左边是误差评分和,加号右边是分解后参数的平方。一个负责模型的偏差,一个负责模型的方差。偏差大的模型欠拟合,方差大的模型过拟合。
有了这个目标后,就要用到优化算法找到能使它最小的参数。优化方法常用的有两个:一个是随机梯度下降(SGD),另一个是交替最小二乘(ALS)。
在实际应用中,交替最小二乘更常用一些,这也是社交巨头Facebook在他们的推荐系统中选择的主要矩阵分解方法,今天,我就专门聊一下交替最小二乘求矩阵分解。
交替最小二乘原理(ALS)
交替最小二乘的核心是交替,什么意思呢?你的任务是找到两个矩阵P和Q,让他们相乘后约等于原矩阵R:
R
m
∗
n
=
P
m
∗
k
∗
Q
n
∗
k
T
R_{m * n} =P_{m * k} * Q_{n * k}^{T}
Rm∗n=Pm∗k∗Qn∗kT
难就难在,P和Q两个都是未知的,如果知道其中一个的话,就可以按照线性代数标准解法求得,比如知道了Q,那么P就可以这样算:
P
m
∗
k
=
R
m
∗
n
∗
Q
n
∗
k
−
1
P_{m*k} =R_{m*n} * Q_{n*k}^{-1}
Pm∗k=Rm∗n∗Qn∗k−1
也就是R矩阵乘以Q矩阵的逆矩阵就得到了结果;反之如果知道了P矩阵,求解Q矩阵也是一样。
交替最小二乘法通过迭代的方式解决了这个难题,具体步骤如下:
1、初始化随机变量Q里面的元素值;
2、把Q矩阵当做已知的,直接用线性代数的方法求得矩阵P;
3、得到了矩阵P后,把p当做已知的,故技重施,回去求解矩阵Q;
4、上面两个过程交替进行,一直到误差可以接收为止。
交替最小二乘法有以下几个优点:
1、在交替的其中一步,也就是假设已知其中一个矩阵求解另一个时,要优化的参数是很容易并行化的;
2、在不那么稀疏的数据集合上,交替最小二乘通常比随机梯度下降要更快地得到结果,事实上这一点就是关于隐式反馈的内容。
隐式反馈
矩阵分解算法,是为解决评分预测问题而产生的。比如说,预测用户会给商品打几颗星,然后把用户可能打高星的商品推荐给用户,
然而事实上却是,用户首先必须先去浏览商品,然后是购买,最后才可能打分。
相比“预测用户会打多少分”,“预测用户会不会去浏览”更加有意义,而且,用户浏览数据远远多于打分评价数据。也就是说,实际上推荐系统关注的是预测行为,也就是隐式反馈。
那如何从解决评分预测问题转向解决预测行为上来呢?这就是另一类问题了:One-Class。
如果把预测用户行为看成一个二分类问题,猜用户会不会做某件事,但实际上收集到的数据只是明确的一类:用户干了某件事,而用户明确不干某件事的数据却没有明确表达。这就是One-Class的由来,One-Class数据也是隐式反馈的通常特点。
对隐式反馈的矩阵分解,需要将交替最小二乘做一些改进,改进后的算法叫做加权交替最小二乘:Weighted-ALS。
这个加权要从哪说起?用户对物品的隐式反馈,通常是可以多次的,后台记录了你查看过这件商品多少次,查看次数越多,就代表你越喜欢这个。也就是说,行为的次数是对行为的置信度反应,也就是所谓的加权。
加权交替最小二乘对隐式反馈:
1、如果用户对物品无隐式反馈则认为评分为0;
2、如果用户对物品有至少一次隐式反馈则认为评分是1,次数作为评分的置信度。
那现在的目标函数在原来的基础上变成这样:
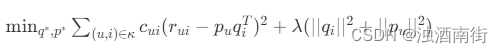
多出来的Cui就是置信度,在计算误差时考虑反馈次数,次数越多,就越可信。置信度一般也不是直接等于反馈次数,根据一些经验,置信度Cui这样计算:
C
u
i
=
1
+
α
C
C_{ui}=1+αC
Cui=1+αC
其中α是一个超参数,需要调教,默认值取40就可以了,C是次数。
这里又引出另一个问题,那些没有反馈的缺失值,就是在我们的假设下,取值为0的评分非常多,有两个原因导致在实际使用时需要注意这个问题:
1、本身隐式反馈就只有正类别是确定的,负类别是假设的。
2、这会导致正负类别非常不平衡,严重倾斜到0评分这边。
因此,不能使用所有的缺失值作为负类别,矩阵分解的初心就是要填充这些值,应对这个问题的做法是负样本采样:挑选一部分缺失值作为负类别即可。
怎么挑?有两个方法:
1、随机均匀采样和正类别一样多;
2、按照物品的热门程度采样;
实践证明,第二种比较靠谱。现在,你想一下,在理想的情况下,什么样的样本最适合做负样本呢?
就是展示给用户了,他也知道了这个物品的存在了,但就是没有对其作出任何反馈。问题是:很多时候我们不能确定用户没有意识到物品的存在呢?还是知道物品的存在而不感兴趣呢?
因此按照物品热门程度采样的思想就是:一个越热门的物品,用户越可能知道它的存在。那这种情况下,用户还没对它有反馈就表明:这很可能就是真正的负样本。
实际上按照热门程度采样构建负样本,和前面提到的文本算法Word2vec学习过程,都用到了类似的负样本采样技巧。
推荐计算
在得到了分解后的矩阵后,相当于每个用户得到了隐因子变量,这是一个稠密向量,用于代表他的兴趣。同时每个物品也得到了一个稠密向量,代表它的语义或主题。两者是一一对应的,用户的兴趣就是表现在物品的语义维度上的。
貌似让用户和物品的隐因子向量两两相乘,计算点积即可得到所有的推荐结果了。实际上复杂度还是很高,尤其对于用户数量和物品数量都巨大的应用,就更不现实。于是Facebook提出了两种解决办法:
第一种,利用一些专门设计的数据结构存储所有物品的隐因子向量,从而实现通过一个用户向量可以返回最相似的k个物品。
于是Facebook给出了自己的开源实现Faiss,类似的开源实现还有Annoy,KGraph,NMSLIB。
其中Facebook开源的Faiss和NMSLIB(Non-Metric Space Library ) 都用到了 ball tree 来存储物品向量。
如果需要动态增加新的物品向量到索引中,推荐使用Faiss ,如果不是,推荐使用NMSLIB或者KGraph。 用户向量则可以存在内存数据中,这样可以在用户访问时,实时产生推荐结果。
第二种:就是拿着物品的隐因子向量先做聚类,海量的物品会减少为少量的聚类。 然后再逐一计算用户和每个聚类中心的推荐分数,给用户推荐物品就变成了给用户推荐物品聚类。
得到物品推荐的聚类后,再从每个聚类中挑选少许几个物品作为最终推荐结果。这样做的好处除了大大减小推荐计算向量之外,还可以控制推荐结果的多样性,因为可以控制在每个类比中选择的物品数量。
总结
在真正的推荐系统的实际应用中,评分预测实际上场景很少,而且数据也很少。因此,相比预测评分,预测用户会对物品干出什么事,会更加有效。
然而这就需要对矩阵分解做一些改进,加权交替最小二乘就是改进后的矩阵分解算法,被Facebook采用在了他们的推荐系统中,这篇文章里,我也详细地解释了这一矩阵分解算法在落地时的步骤和注意事项。
其中,针对One-Class 这种集合,一种常用的负采样构建方法是根据物品的热门程度采样。