文章目录
- 权值线段树
- 添加一个数字
- 求某数出现的次数
- 查询一段区间中数字出现的次数
- 查询整个值域中第k小的数
- 查询整个值域中第k大的数
- 例子:求逆序对
关于基本线段树与线段树的模板,请看我们之前发布的博客:
线段树入门详解
维护加法乘法,区间修改查询的线段树模板
请注意,本节的前置知识是必须懂得基础线段树的操作。
权值线段树
什么是权值线段树,顾名思义就是节点带权值的线段树,我们基本的线段树的节点由一个区间范围和一个记录最大最小值或者区间和的数值组成。 但是我们的权值线段树的节点是由权值构成的,即数组中出现的某一个数字的次数,就可以看作一个权值,因此就可以存储在权值线段树中当作这个线段的节点,这就是权值线段树。
对于一个给定的数组:
- 普通线段树可以维护某个子数组中数的和
- 而权值线段树可以维护某个区间内数组元素出现的次数。
请注意:权值线段树维护的是值域,对于权值线段树来说空间往往是其限制因素,对于le9以上的数据,我们基本不可能做到维护1e9以上的数据,因此往往需要 离散化+线段树,不光是权值线段树,基本上所有的线段树都需要离散数据,如果值域小的话则不需要。
关于离散化数据的n种方式:数据的离散化方式
权值线段树对于处理值域上的值出现的次数,即计数问题有着很大的优势。
权值线段树的作用领域有哪些???
- 求一段区间的某个数字出现的次数
- 查询整体区间的第k大/小的值(注意是整体区间(整个值域),等会你就会发现权值线段树与主席树的区别,主席树可以求得任意区间的第k大/小的值)
添加一个数字
往权值线段树中添加一个数字,则节点记录的就是这个数字出现的次数,因此递归到指定区间后,次数加1即可。
//添加数字
void update(int i, int pl, int pr, int x)
{
if (pl == pr)
{
sum[i]++; //到达了叶子节点,叶子节点维护的就是这个数字出现的次数
return;
}
int mid = (pl + pr) >> 1;
if (x <= mid) update(i << 1, pl, mid, x);
if (x > mid) update(i << 1 | 1, mid + 1, pr, x);
sum[i] = sum[i << 1] + sum[i << 1 | 1];
}
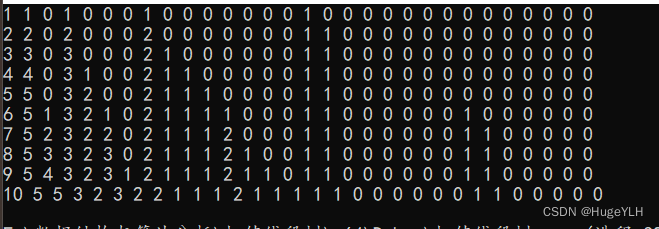
测试代码如下:结果肯定是没有问题的,每添加一个数字,每一个叶子节点就会更新为这个值出现的次数,根节点表示这个这个值域中的数字出现的次数
build(0,1,10);
for (int i = 1; i <= 10; i++)
{
update(1, 1, 10, i);
for (int i = 1; i <= 30; i++)
{
cout << sum[i] << " ";
}
cout << endl;
}
求某数出现的次数
- 递归寻找表示此数的区间
- pl==pr表示到达叶子节点,返回sum[i]即可
int query(int i, int pl, int pr,int x)
{
//x表示要查询的值
if (pl == pr)
{
return sum[i];
}
int ans = 0;
int mid = (pl + pr) >> 1;
if (x <= mid) ans = query(i << 1, pl, mid, x);
if (x > mid) ans = query(i << 1 | 1, mid + 1, pr, x);
return ans;
}
查询一段区间中数字出现的次数
- 给出一段区间: [L,R] 为 [1,5] ,在权值线段树中查询 在这个区间里的所有的数出现的总次数,即1,2,3,4,5在权值线段树中从共出现了多少次
- 递归左右子树,找到完全覆盖的子区间
- ans要 +=,否则会在一次查找后把ans原值覆盖。
int query(int i, int pl, int pr, int L, int R)
{
//[L,R]表示要查询的区间
if (L <= pl && pr <= R)
{
return sum[i];
}
int ans = 0;
int mid = (pl + pr) >> 1;
if (L <= mid) ans += query(i << 1, pl, mid, L, R);
if (R > mid) ans += query(i << 1 | 1, mid + 1, pr, L, R);
return ans;
}
查询整个值域中第k小的数
int query2(int i, int pl, int pr, int k)
{
/*
第k小的数:
首先求出左右孩子节点的元素个数 Ln=sum[i<<1] Rn=sum[i<<1|1]
1. 如果k小于等于Ln,说明第k小的元素在左子树中,则递归到左子树
2. 如果k大于Ln,说明第k小的数字在右子树中,则递归到右子树,同时注意如果k=8,左子树元素有5个,则在右子树中相当于寻找第 k-Ln 个,即第3个元素
*/
if (pl == pr)
{
return pl;
}
int ans = 0;
int mid = (pl + pr) >> 1;
int Ln = sum[i << 1]; //左孩子表示的元素个数
int Rn = sum[i << 1 | 1];//右孩子表示的元素个数
if (k <= Ln) ans = query2(i << 1, pl, mid, k); //左子树
else ans = query2(i << 1 | 1, mid + 1, pr, k - Ln); //右子树
return ans;
}
查询整个值域中第k大的数
注意:我们要求的是整个值域中,而不是任意区间。
int query3(int i, int pl, int pr, int k)
{
/*
第k大的数: 相当于逆着求第k小的数
首先求出左右孩子节点的元素个数 Ln=sum[i<<1] Rn=sum[i<<1|1]
1. 如果k小于等于Rn,则第k大的元素在右子树中,递归右子树
2. 如果k大于Rn,则第k大元素在左子树中,同时注意k=4 右子树元素有3个,则在左子树中相当于寻找第 k-Rn 个元素,即寻找第1个元素
*/
if (pl == pr)
{
return pl;
}
int ans = 0;
int mid = (pl + pr) >> 1;
int Ln = sum[i << 1]; //左孩子表示的元素个数
int Rn = sum[i << 1 | 1];//右孩子表示的元素个数
if (k <= Rn) ans = query3(i << 1|1, mid+1, pr, k); //右子树
else ans = query3(i << 1, pl, mid, k - Rn); //左子树
return ans;
}
注意:值线段树的每一个节点从左往右满足递增,因此较大的元素一定在右子树中,较小的元素一定在左子树中
例子:求逆序对
题目传送门:逆序对
对于题目我不再描述,我们可以知道,逆序对的几种做法:
- 归并排序
- 树状数组
- 线段树(权值线段树)
注意:用权值线段树求逆序对相对比树状数组和归并排序很慢!!!!!!!!!!
本例只是为了演示权值线段树的用法!!
思路
- 离散化数据,然后把离散化后的数据逐一添加到权值线段树中
- 每次添加完成后,求 nums[i]+1 - N 这个范围内的元素的个数,比nums[i]大,即求得是这个nums[i] 的逆序对的数量。
用到了上面的 《查询一段区间中数字出现的次数》的代码
AC code
注意:在权值线段树中build函数可有可无,我们主要是利用update添加一个元素
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using DB = double;
using PI = pair<int, int>;
using PL = pair<LL, LL>;
template<typename T> using v = vector<T>;
constexpr auto INF = 0X3F3F3F3F;
template<typename T1,typename T2> using umap = unordered_map<T1, T2>;
#define ic std::ios::sync_with_stdio(false);std::cin.tie(nullptr)
template <typename ConTainermap> void dbgumap(ConTainermap c); //output umap
template <typename _Ty> void dbg(_Ty nums[],int n);
#if 1
#define int LL
#endif
inline int read(); //fast input
inline void write(int x); //fast output
//TODO: Write code here
int n;
const int N=5e5+10;
int nums[N<<2],tree[N<<2],temp[N<<2];
void build(int i,int pl,int pr)
{
if (pl==pr)
{
tree[i]=0; //元素出现的次数++
return;
}
int mid=(pl+pr)>>1;
build(i<<1,pl,mid);
build(i<<1|1,mid+1,pr);
tree[i]=tree[i<<1]+tree[i<<1|1];
}
//更新权值线段树: 添加元素
void update(int i,int pl,int pr,int num)
{
if (pl==pr)
{
tree[i]++; //元素出现的次数++
return;
}
int mid=(pl+pr)>>1;
if (num<=mid) update(i<<1,pl,mid,num);
if (num>mid) update(i<<1|1,mid+1,pr,num);
//push_up更新
tree[i]=tree[i<<1]+tree[i<<1|1];
}
//查询一段区间中数字出现的次数
int query(int i,int pl,int pr,int L,int R)
{
if (L<=pl && pr<=R)
{
return tree[i]; //找到此元素节点
}
int ans=0;
int mid=(pl+pr)>>1;
if (L<=mid) ans+=query(i<<1,pl,mid,L,R);
if (R>mid) ans+=query(i<<1|1,mid+1,pr,L,R);
return ans;
}
signed main()
{
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>nums[i];
temp[i]=nums[i];
}
sort(temp+1,temp+1+n);
int len=unique(temp+1,temp+1+n)-temp-1;
build(1,1,N);
int ans=0;
for (int i=1;i<=n;i++)
{
nums[i]=lower_bound(temp+1,temp+1+len,nums[i])-temp;
//每次添加一个元素到权值线段树中
update(1,1,N,nums[i]);
ans+=query(1,1,N,nums[i]+1,N);
}
cout<<ans;
return 0;
}
template <typename _Ty>
void dbg(_Ty nums[],int n)
{
for (int i=1;i<=n;i++)
{
cout<<nums[i]<<" ";
}
cout<<endl;
}
template <typename ConTainermap>
void dbgumap(ConTainermap c)
{
for (auto& x:c)
{
cout<<"key:"<<x.first<<" val:"<<x.second<<endl;
}
}
inline int read()
{
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9')
{
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
{
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
inline void output(int x)
{
static int sta[35];
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
while (top) putchar(sta[--top] + 48);
}