🍭 大家好这里是清隆学长 ，一枚热爱算法的程序员

✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解

💻 ACM银牌🥈| 多次AK大厂笔试 ｜ 编程一对一辅导

👏 感谢大家的订阅➕ 和 喜欢💗

📎在线评测链接

K小姐和A先生的聚餐计划(200分)

🌍 评测功能需要 订阅专栏 后私信联系清隆解锁～

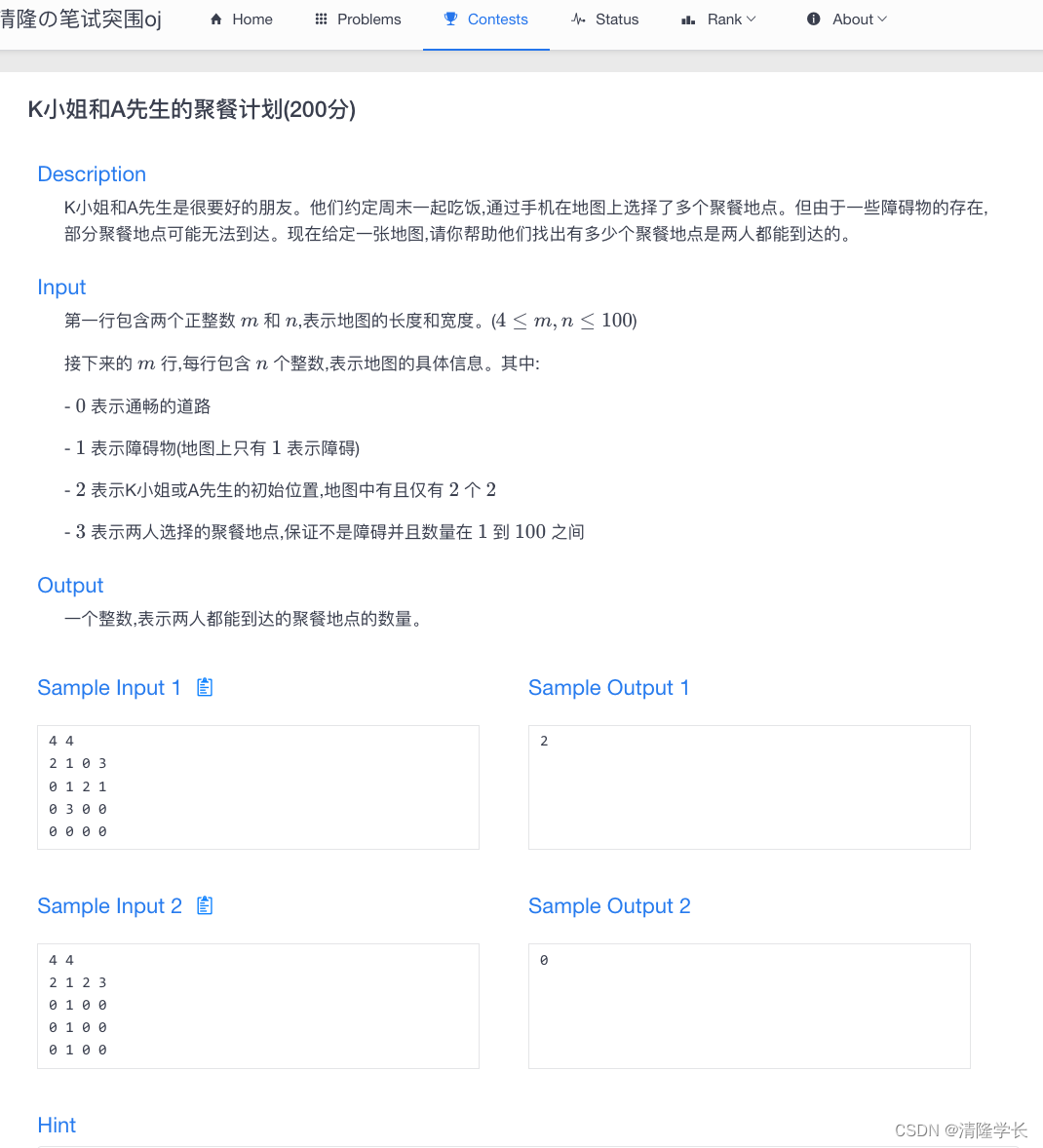
🍓OJ题目截图

✈️ K小姐和A先生的聚餐计划

问题描述

K小姐和A先生是很要好的朋友。他们约定周末一起吃饭,通过手机在地图上选择了多个聚餐地点。但由于一些障碍物的存在,部分聚餐地点可能无法到达。现在给定一张地图,请你帮助他们找出有多少个聚餐地点是两人都能到达的。

输入格式

第一行包含两个正整数 $m$ 和 $n$,表示地图的长度和宽度。($4\le m,n\le 100$)

接下来的 $m$ 行,每行包含 $n$ 个整数,表示地图的具体信息。其中:

• $0$ 表示通畅的道路
• $1$ 表示障碍物(地图上只有 $1$ 表示障碍)
• $2$ 表示K小姐或A先生的初始位置,地图中有且仅有 $2$ 个 $2$
• $3$ 表示两人选择的聚餐地点,保证不是障碍并且数量在 $1$ 到 $100$ 之间

输出格式

一个整数,表示两人都能到达的聚餐地点的数量。

样例输入

4 4
2 1 0 3
0 1 2 1
0 3 0 0
0 0 0 0

样例输出

2

样例输入

4 4 
2 1 2 3
0 1 0 0
0 1 0 0 
0 1 0 0

样例输出

0

数据范围

• $4\le m,n\le 100$
• 聚餐地点数量在 $1$ 到 $100$ 之间
• 障碍物在地图上用 $1$ 表示,非障碍物不会是 $1$
• 保证有且仅有 $2$ 个初始位置

题解

本题可以用 BFS 来解决。我们分别从K小姐和A先生的位置开始进行 BFS 遍历,对于每个遍历到的聚餐地点,将其记录在一个哈希表中,哈希表的键为聚餐地点的坐标,值为能到达该地点的人数。

遍历结束后,我们再遍历哈希表,统计所有值为 $2$ 的键的数量,即为两人都能到达的聚餐地点数量。

时间复杂度 $O(mn)$,空间复杂度 $O(mn)$。

参考代码

• Python

n, m = map(int, input().split())
grid = [list(map(int, input().split())) for _ in range(n)]

dx = [0, 0, 1, -1]
dy = [1, -1, 0, 0]
res = {}

def bfs(x, y, vis):
    queue = [(x, y)]
    vis[x][y] = 1
    while queue:
        x, y = queue.pop(0)
        if grid[x][y] == 3:
            res[(x, y)] = res.get((x, y), 0) + 1
        for i in range(4):
            nx, ny = x + dx[i], y + dy[i]
            if 0 <= nx < n and 0 <= ny < m and vis[nx][ny] == 0 and grid[nx][ny] != 1:
                queue.append((nx, ny))
                vis[nx][ny] = 1

for i in range(n):
    for j in range(m):
        if grid[i][j] == 2:
            bfs(i, j, [[0] * m for _ in range(n)])

ans = sum(1 for v in res.values() if v > 1)
print(ans)

• Java

import java.util.*;

public class Main {
    static int n, m;
    static int[][] grid;
    static int[] dx = {0, 0, 1, -1};
    static int[] dy = {1, -1, 0, 0};
    static Map<String, Integer> res = new HashMap<>();

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();
        grid = new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                grid[i][j] = sc.nextInt();
            }
        }
        
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (grid[i][j] == 2) {
                    bfs(i, j, new int[n][m]);
                }
            }
        }

        int ans = 0;
        for (int v : res.values()) {
            if (v > 1) ans++;
        }
        System.out.println(ans);
    }

    static void bfs(int x, int y, int[][] vis) {
        Queue<int[]> queue = new LinkedList<>();
        queue.offer(new int[]{x, y});
        vis[x][y] = 1;
        
        while (!queue.isEmpty()) {
            int[] curr = queue.poll();
            x = curr[0]; y = curr[1];
            if (grid[x][y] == 3) {
                String key = x + "," + y;
                res.put(key, res.getOrDefault(key, 0) + 1);
            }
            for (int i = 0; i < 4; i++) {
                int nx = x + dx[i], ny = y + dy[i];
                if (0 <= nx && nx < n && 0 <= ny && ny < m 
                        && vis[nx][ny] == 0 && grid[nx][ny] != 1) {
                    queue.offer(new int[]{nx, ny});
                    vis[nx][ny] = 1;
                }
            }
        }
    }
}

• Cpp

#include <iostream>
#include <queue>
#include <unordered_map>
#include <vector>
using namespace std;

const int maxn = 110;
int n, m;
int grid[maxn][maxn];
int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};
unordered_map<string, int> res;

void bfs(int x, int y, vector<vector<int>>& vis) {
    queue<pair<int, int>> q;
    q.push({x, y});
    vis[x][y] = 1;
    
    while (!q.empty()) {
        auto [x, y] = q.front(); q.pop();
        if (grid[x][y] == 3) {
            res[to_string(x) + "," + to_string(y)]++;
        }
        for (int i = 0; i < 4; i++) {
            int nx = x + dx[i], ny = y + dy[i];
            if (nx >= 0 && nx < n && ny >= 0 && ny < m 
                    && !vis[nx][ny] && grid[nx][ny] != 1) {
                q.push({nx, ny});
                vis[nx][ny] = 1;
            }
        }
    }
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grid[i][j];
        }
    }
    
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grid[i][j] == 2) {
                vector<vector<int>> vis(n, vector<int>(m));
                bfs(i, j, vis);
            }
        }
    }
    
    int ans = 0;
    for (auto [_, cnt] : res) {
        if (cnt > 1) ans++;
    }
    cout << ans << endl;
    
    return 0;
}