1.题目

有 N 个瓶子，编号 1∼N，放在架子上。

比如有 5个瓶子：

2 1 3 5 4

要求每次拿起 2 个瓶子，交换它们的位置。

经过若干次后，使得瓶子的序号为：

1 2 3 4 5

对于这么简单的情况，显然，至少需要交换 2次就可以复位。

如果瓶子更多呢？你可以通过编程来解决。

输入格式
第一行包含一个整数 N，表示瓶子数量。

第二行包含 N 个整数，表示瓶子目前的排列状况。

输出格式
输出一个正整数，表示至少交换多少次，才能完成排序。

数据范围
$1\le N\le 10000,$

输入样例1：

5
3 1 2 5 4

输出样例1：

3

输入样例2：

5
5 4 3 2 1

输出样例2：

2

2.基本思想

通过观察可以发现，我们每一个数都必须回到它自己的位置上，比如 1 必须在第一位，2 必须在第二位上

1.暴力枚举

由于每个数必须回到自己的位置，直接从 1 枚举到 n ，如果当前位置的数不等于它的下标，那么我们就必须要把它给替换掉
设当前位置为 i 的话，那么我们就从 i+1开始往后枚举，直到找到对应的 a[j] 和我们的 i 相等，那么我们就把上个数交换，把交换次数++

2.置换群算法/图论

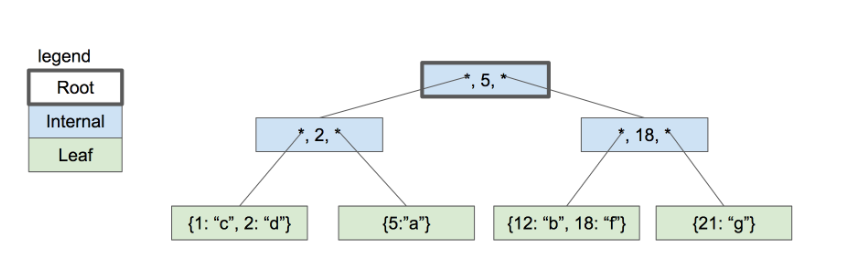
当前位置的 i≠b[i]的话，那么它必然等于其他位置上的 b[i]，那么我们可以利用图的存储方式来描述我们整个数组

分析可知 最终情况为 一个数字一个环，即一个长度为 $n$ 的序列最多存在 $n$ 个环.

且对于每一个环的操作，最多有两种情况，如下图所示，我们要么是在环内操作，要么就是跨环操作（环内操作就是在环内切换连接对象，环外操作就是在环与环之间切换连接对象），即操作一次最多增加一个环，假设当前有k个环，最终序列为n 即 n个环，至少需要n-k
`

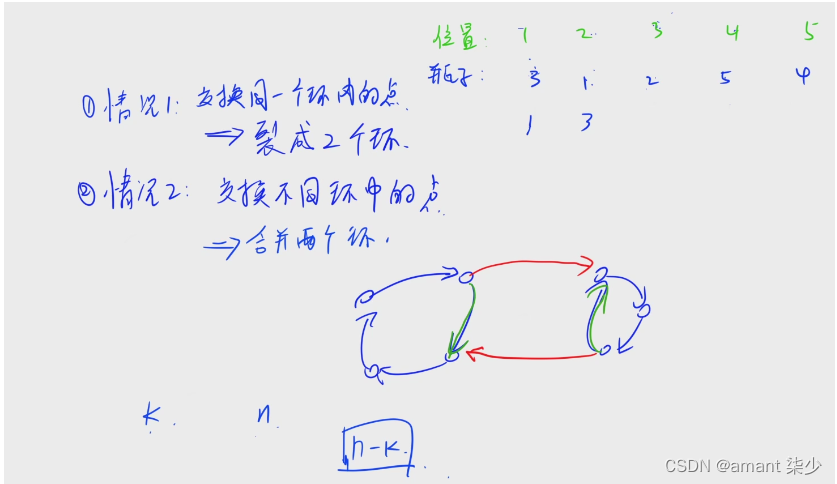
结论：当前k个环 最终 n个环，至少需要n-k个环

3.代码实现

暴力枚举

import java.util.Scanner;

public class Main {
    static Scanner sc = new Scanner(System.in);
    static int a[] = new int[10010];

    public static void main(String[] args) {
        int N = sc.nextInt();
        for (int i = 1; i <= N; i++)
            a[i] = sc.nextInt();

        int cnt = 0;
        for (int i = 1; i <= N; i++) {
            if (i != a[i]) {//当前位置不等 
                for (int j = i + 1; j <= N; j++) {
                    if (i == a[j]) {// 找到 交换
                        int temp = a[i];
                        a[i] = a[j];
                        a[j] = temp;
                        cnt++;
                    }
                }
            }
        }
        System.out.println(cnt);
    }
}

置换群算法

import java.util.Scanner;

public class _1224交换瓶子 {
    static int N = 10010;
    static Scanner sc = new Scanner(System.in);
    static int bottle[] = new int[N];
    static boolean st[] = new boolean[N];

    public static void main(String[] args) {
        int n = sc.nextInt();
        for (int i = 1; i <= n; i++)
            bottle[i] = sc.nextInt();

        int cnt = 0;//统计环数
        for (int i = 1; i <= n; i++) {
            if (!st[i]) {//当前 位置点没被找过 表明在新的环中
                cnt++;
                //把该点 可以到达的所有点进行标记
                for (int j = i; !st[j]; j = bottle[j]) st[j] = true;
            }
        }

        System.out.println(n-cnt);
    }
}