目录
- 核心
- 整体流程
- 分步阐述
- backbone
- 几何关系(创建视锥)和视锥投影到ego
- Voxel Pooling
- Head
- 总结
核心
-
将2D图像特征转换到BEV feature特征
-
该算法是BEV领域中的一大基石
整体流程
-
流程步骤
-
(1)利用backbone获得环视图像(6张图片)的特征;
-
(2)利用几何关系创建每张图片的视锥;
-
(3)利用相机的内外参,将视锥点云投影到ego坐标系下;
-
(4)利用voxel pooling 将环视图像特征转换为BEV特征;
-
(5)BEV encoder 对特征进一步融合,添加network head获得任务结果
-
-
整体流程的示意图如下所示
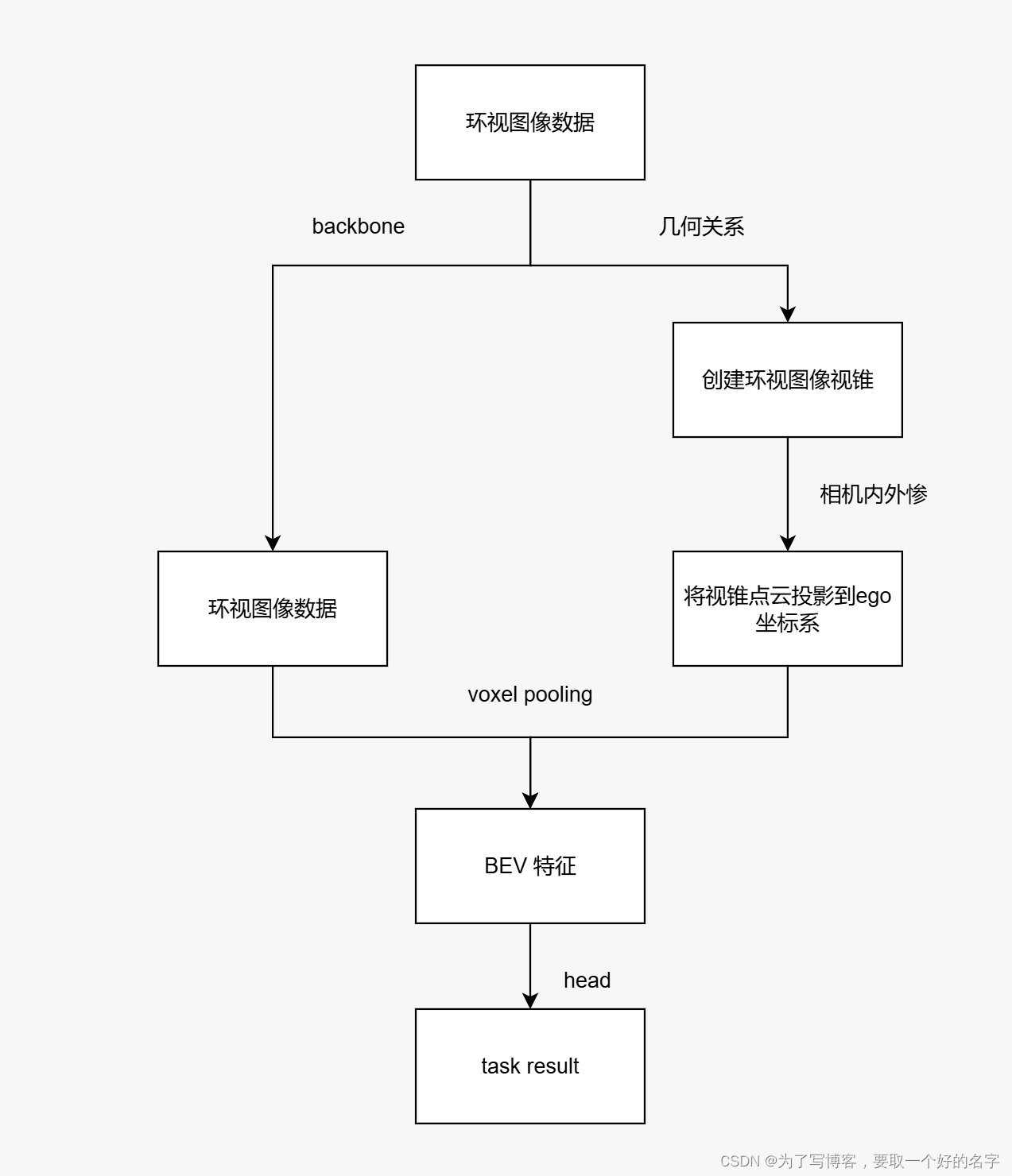
分步阐述
backbone
-
使用EfficientNet网络作为backbone,提取每张图片中的深度特征D=41,语义特征C=61
-
特征图获取流程
-
使用EfficientNet-b0获得特征图:24 x 512 x 8 x 22
-
24:B x N -> B=4,N=6 -> 考虑前面3帧和当前帧图像;6张图片(从该部分看相机的数量只能为6,除非重新训练)
-
fH:8;fW:22
-
-
利用1 x 1卷积将特征图的通道数变为512->105(64+41),24 x 105 x 8 x 22
-
105个特征通道中前64个通道为语义通道,后41个通道为深度通道
-
该部分网络进行了深度估计,通过训练所得
-
-
取出后41个特征通道(深度通道),进行softmax概率估计
-
利用广播机制,将语义通道24 x 64 x 1 x 8 x 22 与深度通道24 x 1 x 41 x 8 x 22进行外积,最终获得24 x 64 x 41 x 8 x 22特征图
-
取出上述某一帧中一张图片的特征图:64 x 41 x 8 x 22,其中的每个特征点的维度为 64 x 41
-
如果该特征点的表征为3m距离的狗,则64个语义通道内,表示狗的语义通道的值最大;3m对应的深度通道距离最大。两个通道利用广播的机制相乘,最大的通道即可表示为3m距离的狗
-
广播机制如下所示,c x a 获得Matirx_(c x a),可以通过该方式获得最大的通道
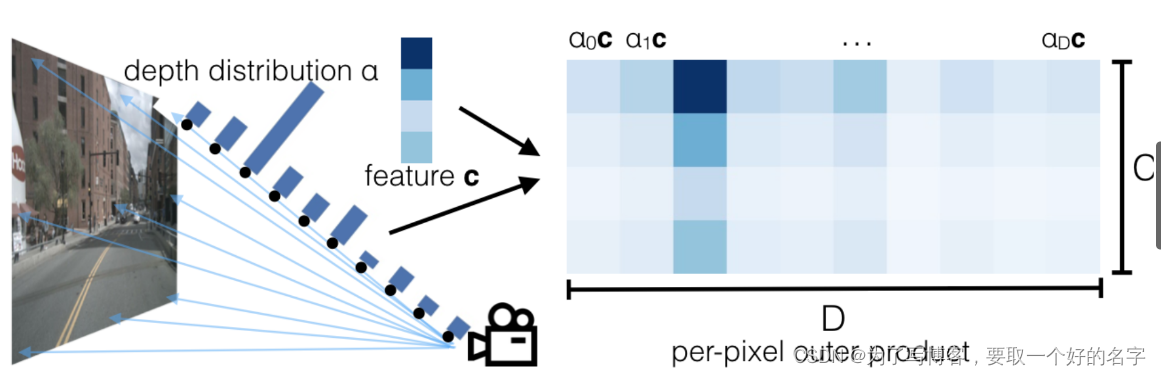
-
-
-
几何关系(创建视锥)和视锥投影到ego
-
总体流程:像素视锥点->剔除图像增强矩阵的影响->生成camera坐标系下的三维视锥点->将视锥点投影到ego坐标系下
-
像素视锥点(u,v,d)的选择:
-
由于最终的特征图尺寸为:8 x 22,则在原始图像上将图片分为8 x 22个图片块(patch)
-
将每个图像块的顶点 + 预设深度(4~45m),即可完成视锥点的构建,形状为D x fH x fW x 3
-
下图所示,第一列为x坐标、第二列为y坐标,第三列为预设深度值
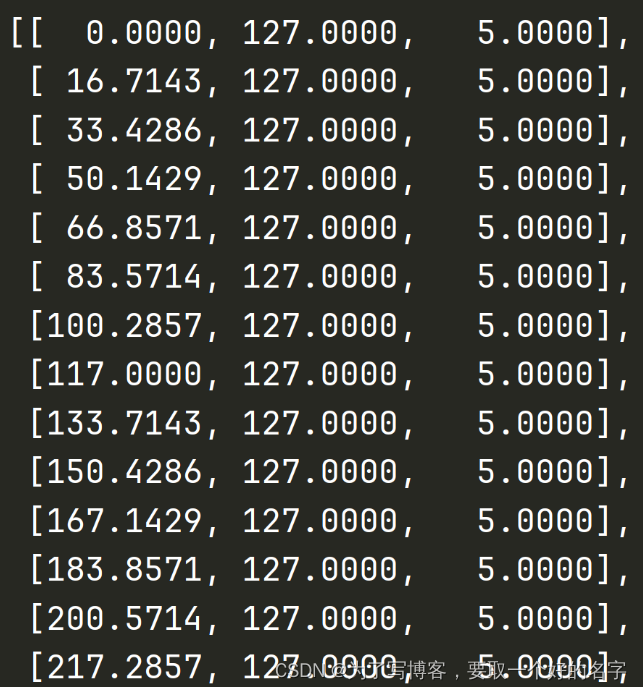
-
代码如下所示:
-

-
剔除增强矩阵的影响
-
目的:例如,可消除图片旋转的影响
-
利用下列公式消除图像增强的像素视锥的影响
p i m g ′ = A − 1 p i m g p^{'}_{img}=A^{-1}p_{img} pimg′=A−1pimg
-
-
获得camera坐标系下视锥点的坐标:
- 利用下列公式,最终才能获得三维坐标系下的视锥点(形状如视锥)
p c a m = I − 1 ( p i m g ∗ d ) p_{cam} = I^{-1}(p_{img}*d) pcam=I−1(pimg∗d)
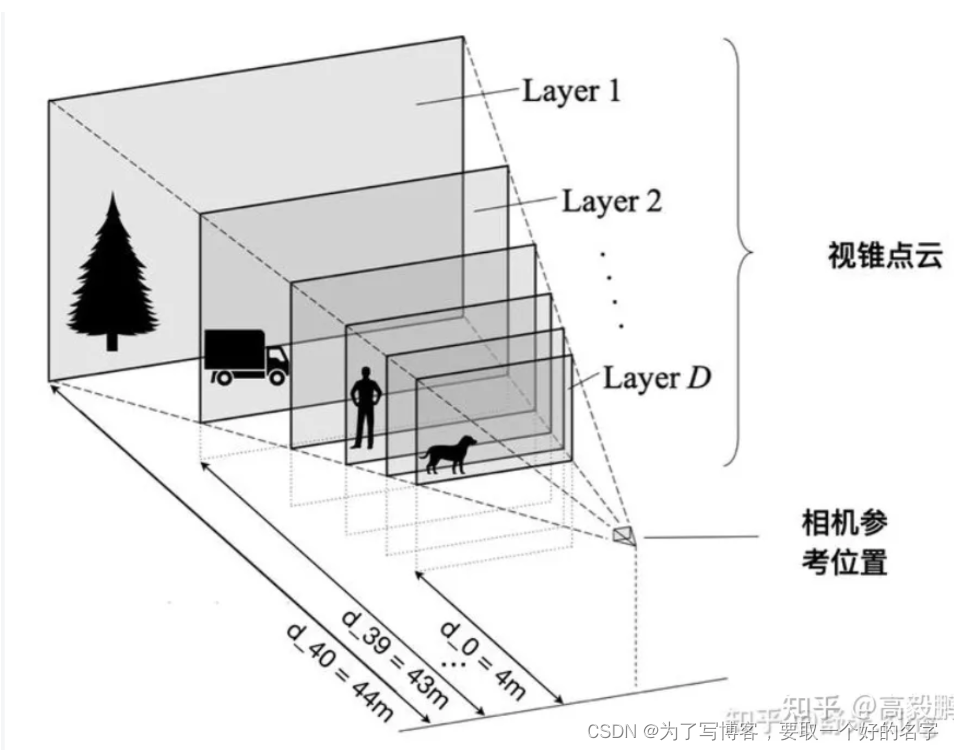
- 利用下列公式,最终才能获得三维坐标系下的视锥点(形状如视锥)
-
将camera坐标系下的视锥点转换到ego坐标系
-
利用camera->ego的TF变换关系能够直接获得,略
-
最终获得的视锥点形状为:B x N x D x H x W x 3
-
Voxel Pooling
-
目的:将环视图像特征转换为BEV特征
-
已有图像特征:B x N x D x H x W x C;视锥点:B x N x D x H x W x 3
-
将图像特征铺开,变为(B x N x D x H x W) x C;将视锥点铺开,变为(B x N x D x H x W) x 3。此时,视锥点与图像特征一一对应,可通过训练获得该内在联系
-
将视锥点分配到预设的BEV网格内,获得栅格坐标。如下公式所示,其中bx:第一个网格的中心点;dx:每个网格的宽度;gemoFeats为视锥点。
- 由于计算栅格坐标时,是取整操作(int),所以存在某几个视锥点位于一个栅格网格内
- 由于预设的xyz范围为[-50, 50]、[-50, 50]、[-10, 10],所以可剔除超出该范围的视锥点。同时,也剔除对应的图像特征点
-
g e m o F e a t = g e m o F e a t − ( b x − d x / 2 ) / d x gemoFeat = gemoFeat - (bx - dx / 2) / dx gemoFeat=gemoFeat−(bx−dx/2)/dx
-
将一个栅格内多个视锥点对应的特征点进行sum pooling,也就是将落在同一个栅格内的多个特征点进行相加操作
-
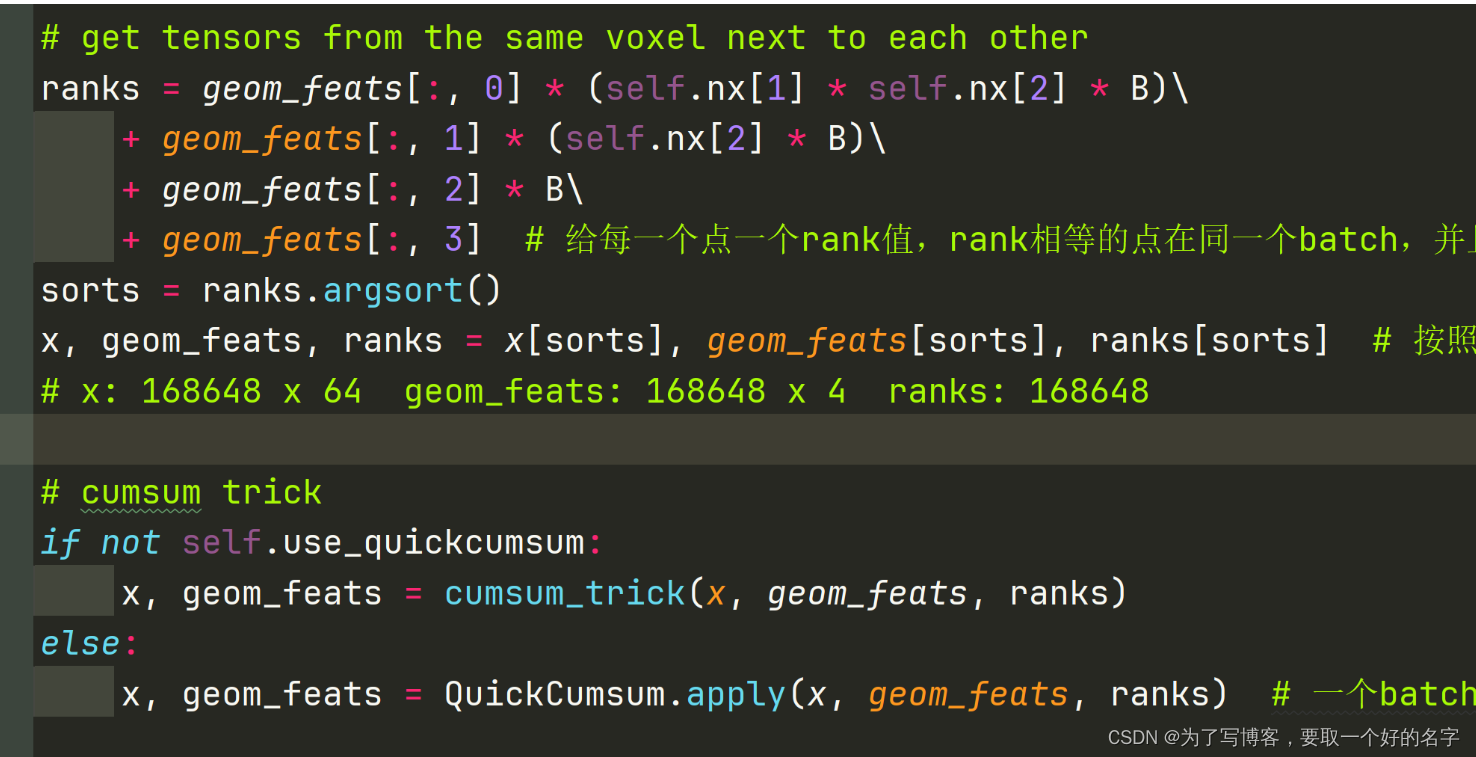
由于特征点的shape大小不一,无法进行批量操作,需要使用如下代码部分进行操作,但实现的效果如上所示。
-
论文中,经过sum pooling后,图像特征的shape为:17375 x 64
-
-
将图像特征按照对应视锥点的位置(即BEV栅格的位置)填入BEV特征图中,获得最终的BEV特征图
- BEV栅格的索引位置远大于图像特征数量

Head
- 依据不同的任务添加不同的Head即可,略
总结
-
LSS算法通过相机内外参显式的获取图像深度。其中,生成视锥点、图像特征转换到BEV特征的思想值得深究
-
不足
-
没有考虑相邻环视图像的特征,图像特征分散获取
-
图像特征重叠时,使用sum pooling的方式,太过简单、粗暴
-