综合练习二
- 1.组合
- 2.目标和
- 3.组合总和
- 4.字母大小写全排列

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
1.组合
题目链接:77. 组合
题目分析:
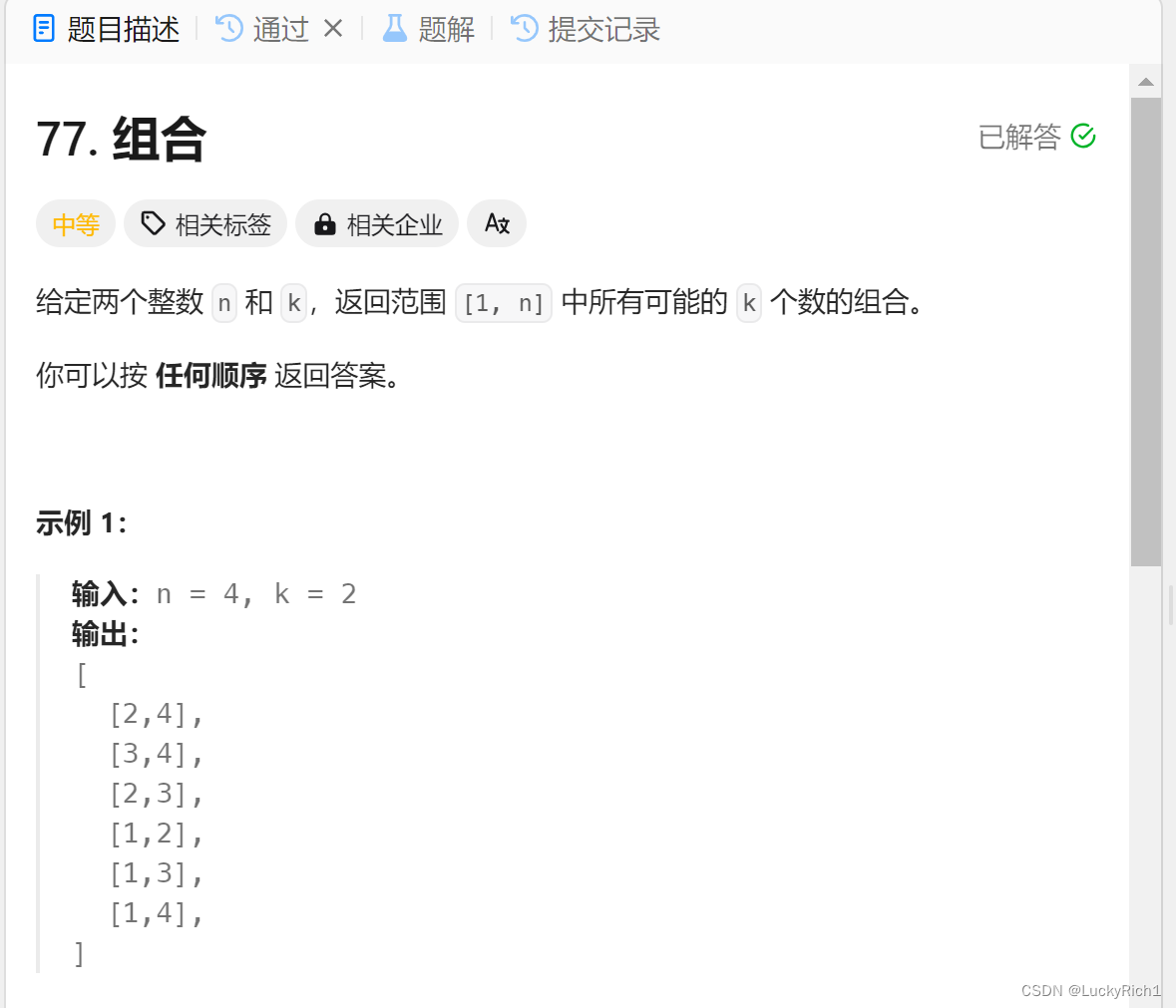
注意这道题结果是不能重复的。如1,2 和 2,1 虽然位置不同但是是同样的组合。

算法原理:
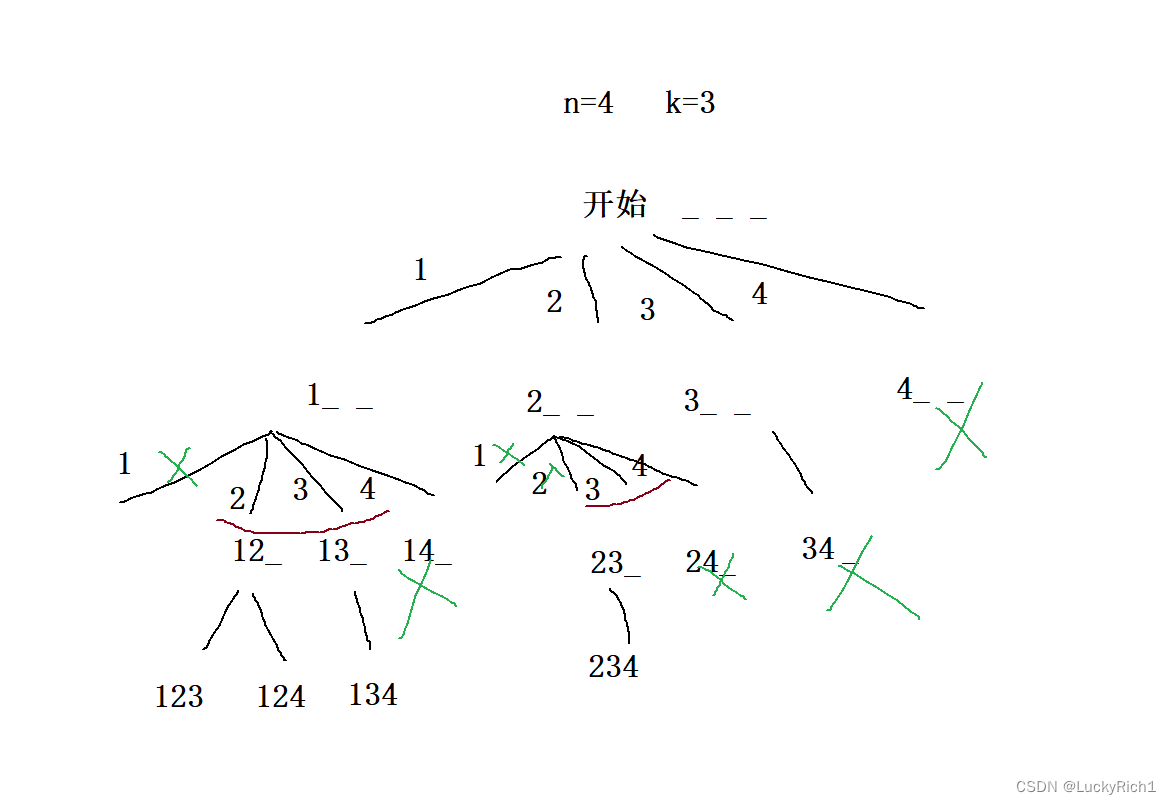
这样的题我们还是画出决策树,然后根据这棵树把所有细节分析清楚
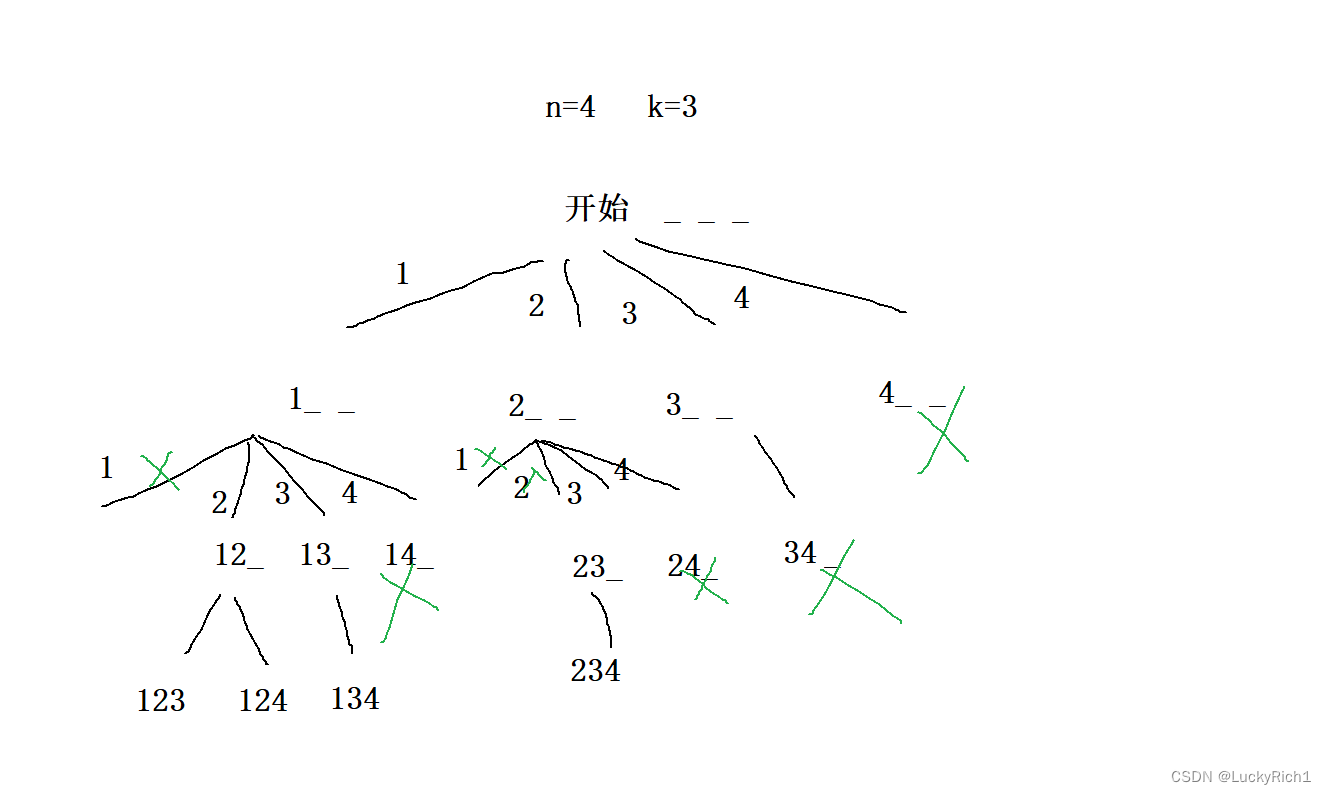
每个位置都有4种选择,首先前面被选种的数字后面就不能再选了,如1,2 和2,1只是位置不同数都是一样的,因此还是重复。其次上每一层都是从上一层被选数字的后面一个开始选的。全局变量,一个ret记录最终结果,一个path记录每条路径的结果。递归函数,给一个pos,每一层都从pos位置开始往后选,dfs(pos),回溯 当递归结束往上返回要恢复现场pop掉path最后一个位置元素,剪枝 用pos控制开始的位置就是剪枝,递归出口 当path.size() == k 就可以把path放到ret里,然后结束本次递归。
class Solution {
vector<vector<int>> ret;
vector<int> path;
int n_,k_;
public:
vector<vector<int>> combine(int n, int k) {
n_=n;k_=k;
dfs(1);
return ret;
}
void dfs(int pos)
{
if(path.size() == k_)
{
ret.push_back(path);
return;
}
for(int i=pos;i<=n_;++i)
{
path.push_back(i);
dfs(i+1);
path.pop_back();//恢复现场
}
}
};
2.目标和
题目链接:494. 目标和
题目分析:

给一个数组,对数组每个数字前面添加 + 或者 - ,串联所有数字构成一个表达式,找出表达式和为目标值有多少种情况。
算法原理:
如果前面做过选子集的问题,这道题思想是一模一样的,找子集其中有一张方法是 这个数字 选or不选,这道题就是 这个数字前面 +or-。我们就根据这个画出决策树。
这里的步骤都不说了,和子集哪里的一模一样。最后到叶子节点这条路径的和加起来等于target,就是一种情况。
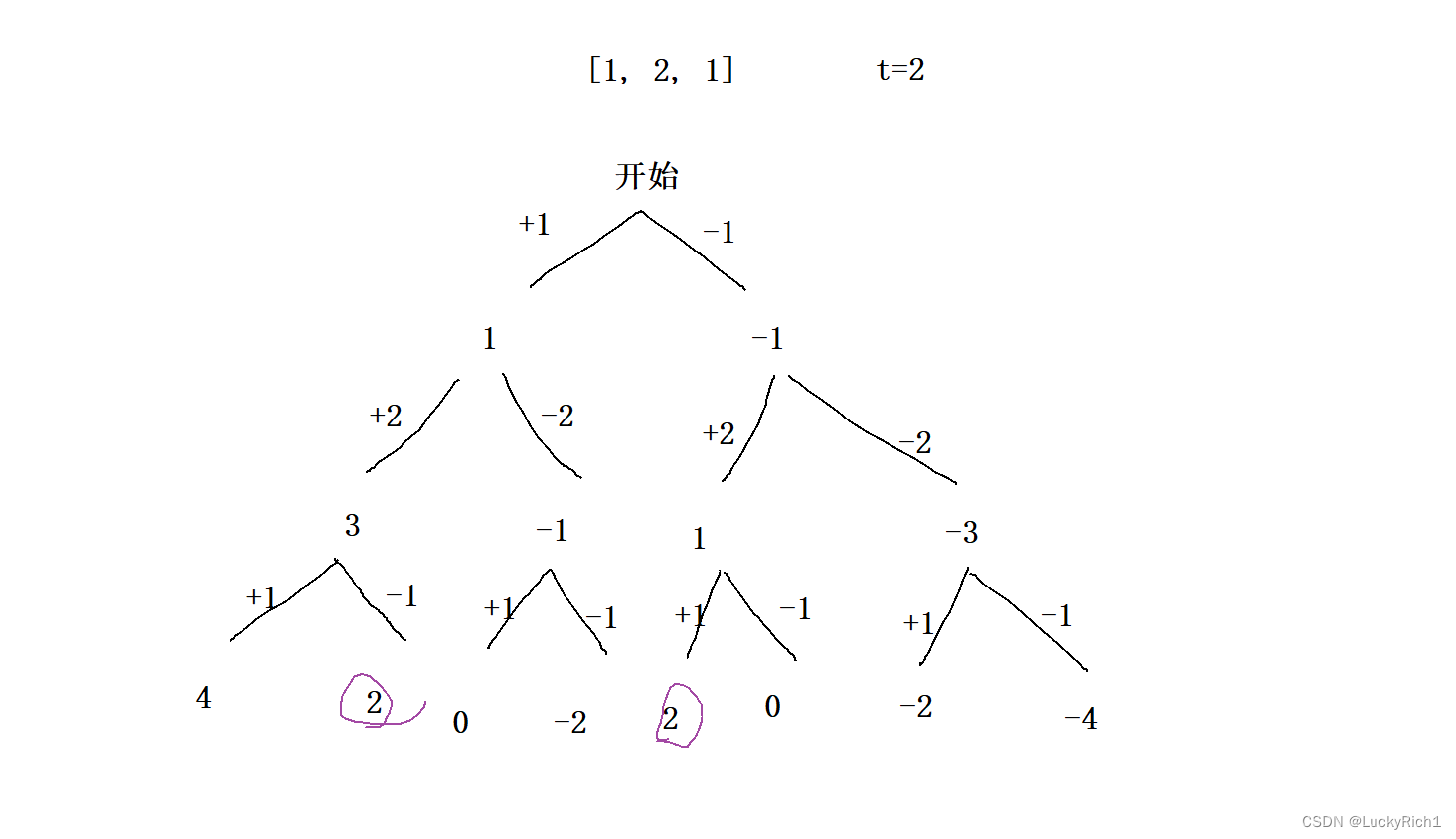
这里写代码有两种形式。
- path 是全局变量的时候的代码
- path 作为参数的代码
可以参考求二叉树所有路径那道题,这道题也是path作为全局变量和作为参数两种不同形式的代码。
path作为全局变量, 需要考虑回溯恢复现场。
path作为参数,不用考虑,因为在递归在向上返回的时候就已经帮助我们回溯恢复现场了。 path作为参数也是有回溯的不过是编译器就可以帮我回溯了。
如果path是一个单独的类型的话,如int类型,你会发现把它放在dfs参数里面写的话,代码比较简洁。如果path是一个数组类型的话,推荐使用全局变量!
path作为全局变量的代码
class Solution {
int ret,path,_target;
public:
int findTargetSumWays(vector<int>& nums, int target) {
_target=target;
dfs(nums,0);
return ret;
}
void dfs(vector<int>& nums,int pos)
{
if(pos == nums.size())
{
if(path == _target) ++ret;
return;
}
// 加法
path+=nums[pos];
dfs(nums,pos+1);
path-=nums[pos];
// 减法
path-=nums[pos];
dfs(nums,pos+1);
path+=nums[pos];
}
};
path作为参数的代码
class Solution {
int ret,_target;
public:
int findTargetSumWays(vector<int>& nums, int target) {
_target=target;
dfs(nums,0,0);
return ret;
}
void dfs(vector<int>& nums,int pos,long path)
{
if(pos == nums.size())
{
if(path == _target) ++ret;
return;
}
// +
dfs(nums,pos+1,path+nums[pos]);
// -
dfs(nums,pos+1,path-nums[pos]);
}
};
3.组合总和
题目链接:39. 组合总和
题目分析:

注意这个数组中的数字,可以无限制重复被选择。但是结果不能有重复的就如下面2,2,3 和 2,3,2是属于同一种组合,只是位置不同罢了。
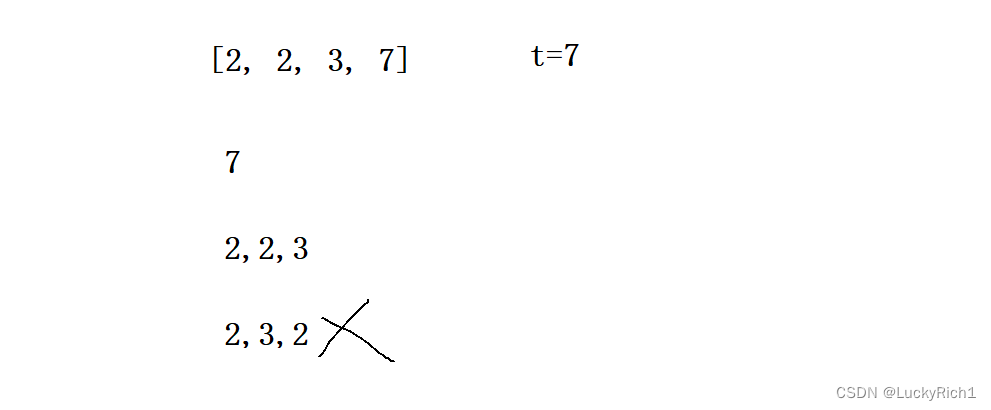
算法原理:
暴力枚举所有情况,根据不同的决策树,我们可以写出不同的代码。就比如
- 根据每个位置选什么的策略 画决策树
- 根据每个数选or不选 画决策树
- 考虑每个数用多少个 画决策树
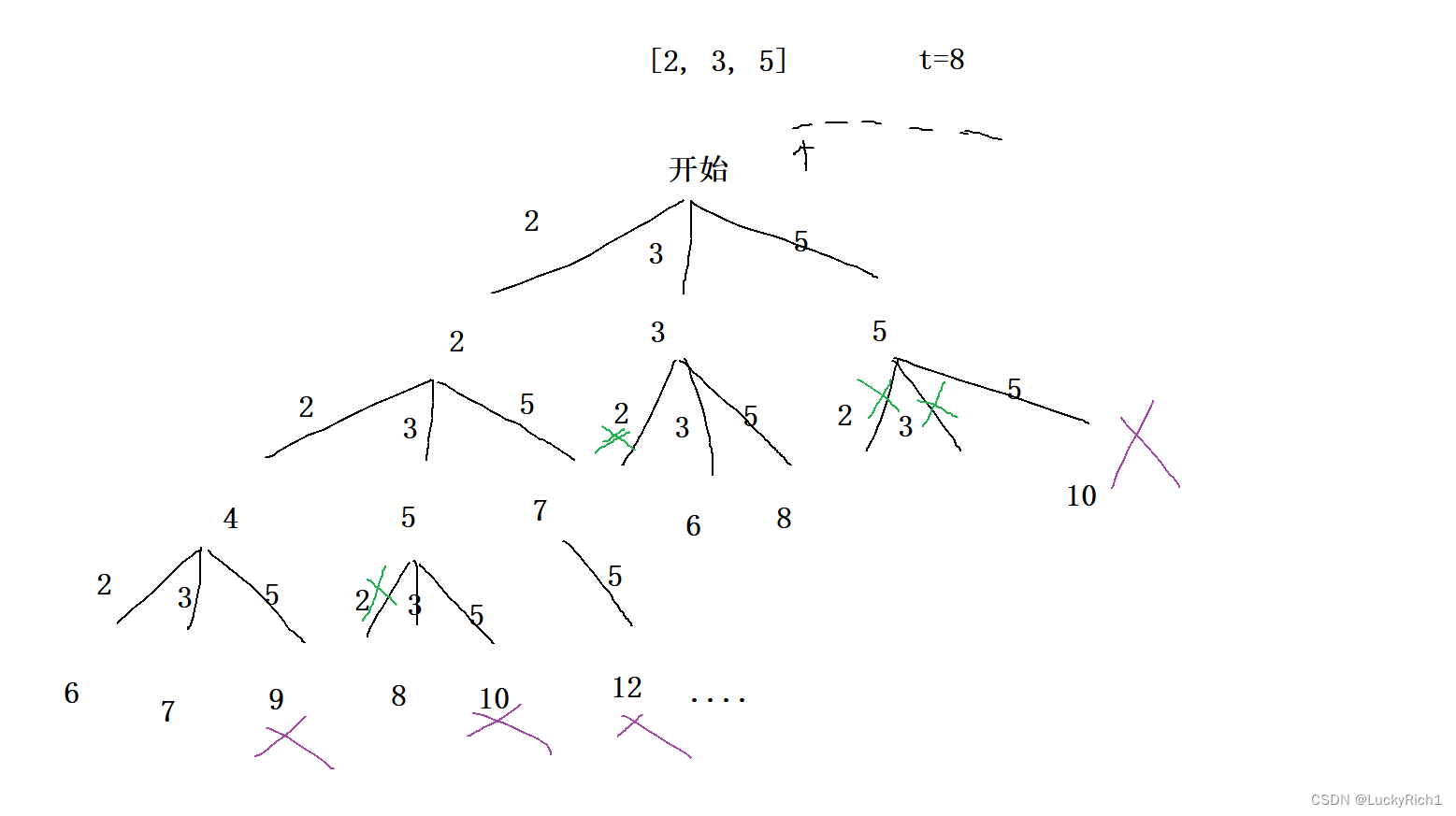
解法一: 根据每个位置选什么的策略 画决策树
每个位置都有三种选择,因为一个数可以被无限制重复选择,所以递归到下一层还可以选。注意3,2 和 2,3 是一样的组合,前面选了后面就不要在选了。并且5,2 和5,3 和2,5 和3,5一样前面选了后面就不要选了。这是一种剪枝情况,还有当一路径的和sum都大于target了就可以结束递归了。这也是一种剪枝情况。
前面我们特别说明一下全局变量的和作为参数的在递归的区别。这里sum求每一条路径的和我们把它作为参数在递归函数中传递,这样每次回溯就不管sum了,而ret和path还是作为全局变量。递归函数 我们发现每次都是从本身位置开始往下选,因此 dfs(nums,pos,sum),回溯 sum不用管,path等到递归返回后pop掉最后一个元素,剪枝已经在递归函数中作为pos传递了 ,递归出口 当sum == target 将path放到ret里然后返回,还有一种情况当sum>target不需要往下递归了和pos == nums.size()也不需要往下递归直接返回;
class Solution {
vector<vector<int>> ret;
vector<int> path;
int aim;
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
aim=target;
dfs(candidates,0,0);
return ret;
}
void dfs(vector<int>& candidates,int pos,int sum)
{
if(sum >= aim)
{
if(sum > aim) return;
if(sum == aim) ret.push_back(path);
return;
}
for(int i=pos;i<candidates.size();++i)
{
path.push_back(candidates[i]);
dfs(candidates,i,sum+candidates[i]);
path.pop_back();//恢复现场
}
}
};
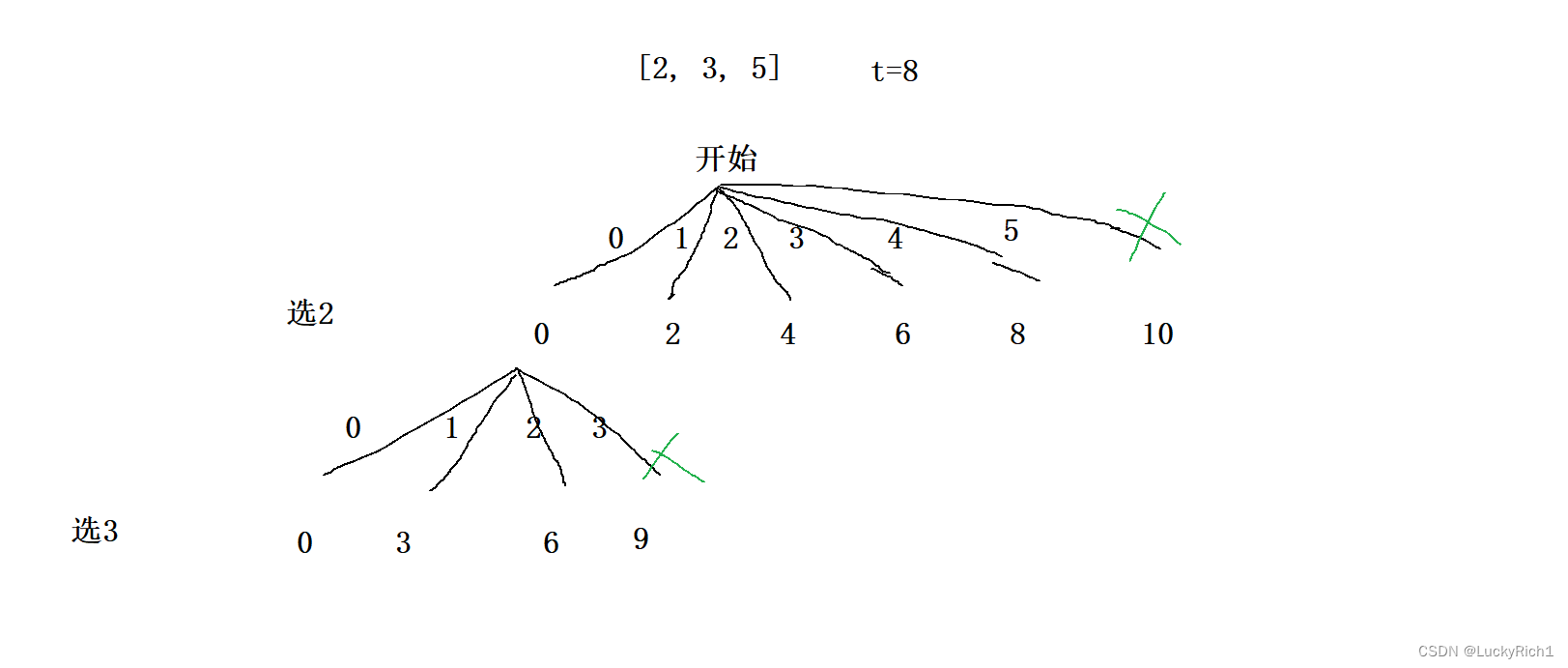
解法二: 考虑每个数用多少个 画决策树
每个数可以被选择0-n次,当被选择n次的和都大于target就不能选选了,也就是说小于或者等于target的时候可以一直选这个数,然后往下递归也是和上面情况一样。这里有个细节要注意,当递归回去的时候,不要直接把path最后一个位置pop掉,而是等到这个数所有情况都选完了然后在pop掉path最后一个元素,因为这个数可以选1次、两次等等,如果选择一次往下走递归回来了你pop掉了,下一次path.push_back()就要放两个这个数,因为我们不先pop,等到最后这个数所有情况搞完返回上一层我们在把前面加入的所有这个数pop掉。
class Solution {
vector<vector<int>> ret;
vector<int> path;
int aim;
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
aim=target;
dfs(candidates,0,0);
return ret;
}
void dfs(vector<int>& candidates,int pos,int sum)
{
if(sum == aim)
{
ret.push_back(path);
return;
}
if(sum > aim || pos == candidates.size()) return;
// 枚举个数
for(int k = 0; k * candidates[pos] + sum <= aim; k++)
{
if(k) path.push_back(candidates[pos]);
dfs(candidates, pos + 1, sum + k * candidates[pos]);
}
// 恢复现场
for(int k=1;k*candidates[pos]+sum <= aim;++k)
{
path.pop_back();
}
}
};
4.字母大小写全排列
题目链接:784. 字母大小写全排列
题目描述:

算法原理:
还是画出决策树,写代码。
对于每个字母我们都有两种选择,要么不变,要么变,小写变大写,大写变小写。对于数字我们不管它。其他的还是和前面的题一模一样。可以用全局path,也可以path当参数用。

class Solution {
vector<string> ret;
string path;
public:
vector<string> letterCasePermutation(string s) {
dfs(s,0);
return ret;
}
void dfs(string& s,int pos)
{
if(pos == s.size())
{
ret.push_back(path);
return;
}
char ch=s[pos];
// 不改变
path.push_back(ch);
dfs(s,pos+1);
path.pop_back();
// 变
if(ch < '0' || ch > '9')
{
if(islower(ch)) ch-=32;
else ch+=32;
path.push_back(ch);
dfs(s,pos+1);
path.pop_back();
}
}
};