前言
你的qq密码是否在圆周率中出现?
一个有意思的编码问题:假设密码是固定位数,设有 n n n位,每位是数字0-9,那么这样最短的“圆周率”的长度是多少?或者说求一个最短的数字串定包含所有密码。
理论
一些定义:
通过图中所有边恰好一次且行遍所有顶点的通路称为欧拉通路;
通过图中所有边恰好一次且行遍所有顶点的回路称为欧拉回路;
具有欧拉回路的无向图称为欧拉图;
具有欧拉通路但不具有欧拉回路的无向图称为半欧拉图。
求欧拉回路/通路,俗称一笔画问题,之前一直以为这个问题十分困难,直到慢慢学习揭开它的真面目。在离散课程中,学习到判断(半)欧拉图的充要条件是顶点的度数满足一定条件。具体如下

必要性比较容易证明,充分性是通过一个构造性证明,大致是首先找到一个回路
C
C
C,若回路
C
C
C中存在顶点
u
u
u有出边不在回路
C
C
C中,则从顶点
u
u
u出发dfs可以回到
u
u
u构成一个回路
C
′
C'
C′,将回路
C
C
C和
C
′
C'
C′合并得到一个新回路,反复操作直到所有边均访问过。
Fleury 算法
之前数学建模了解过一个Fleury算法,大意是桥不能走,个人感觉这不是≈不能走的路不能走!而且图在动态变化怎么动态地维护图中的桥,没有详细了解而且网上相关blog也比较少。

Hierholzer 算法
Hierholzer 算法用于在连通图中寻找欧拉路径,其流程如下:
- 从起点出发,进行深度优先搜索。
- 每次沿着某条边从某个顶点移动到另外一个顶点的时候,都需要删除这条边。
- 如果没有可移动的路径,则将所在节点加入到栈中,并返回。
证明传送门:https://taodaling.github.io/blog/2019/04/25/Hierholzer%E7%AE%97%E6%B3%95/
代码模板
- leetcode 332:你一份航线列表 tickets ,其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。(求有向图的欧拉通路)
- 算法核心:访问前删除边(通常我们通过
vis[]数组标记顶点已访问而不是边),并在顶点所有出边访问完后,入栈记录答案,实际上欧拉通路是递归调用返回路径构成的通路。 - 容器
map嵌套priority_queue的技巧,之前自己灵光一现想到用于将数组下标拓展至负数,这里拓展为string类型,按字典序进行从小到大进行排序,但这种写法仅适用于有向图,STL优先队列没有定义erase操作 - 时间复杂度: O ( m l o g m ) O(mlogm) O(mlogm),其中 m m m 是边的数量。对于每一条边我们需要 O ( l o g m ) O(logm) O(logm) 地删除它,最终的答案序列长度为 m + 1 m+1 m+1,而与 n n n 无关。
- 空间复杂度: O ( m ) O(m) O(m),其中 m m m 是边的数量。我们需要存储每一条边。
unordered_map<string,
priority_queue<string, vector<string>, std::greater<string>>> vec;
vector<string> stk;
void dfs(const string& curr) {
while (vec.count(curr) && vec[curr].size() > 0) {
string tmp = vec[curr].top();
vec[curr].pop();
dfs(tmp);
}
stk.emplace_back(curr);
}
vector<string> findItinerary(vector<vector<string>>& tickets) {
for (auto& it : tickets) {
vec[it[0]].emplace(it[1]);
}
dfs("JFK");
reverse(stk.begin(), stk.end());
return stk;
}
- luogu P2731:求无向图的欧拉通路
- 算法核心:访问前删除边(通常我们通过
vis[]数组标记顶点已访问而不是边),并在顶点所有出边访问完后,入栈记录答案,实际上欧拉通路是递归调用返回路径构成的通路。 - 通过
map<pair<int, int>, int> cnt标记边的访问,这里时间复杂度为 O ( m l o g m ) O(mlogm) O(mlogm),对cnt的自减操作实际在修改rb_tree的值,复杂度为 O ( l o g m ) O(logm) O(logm),和优先队列相同
vector<int> ans;
vector<int> g[2005];
map<pair<int, int>, int> cnt;
int m;
void dfs(int u) {
for (int i = 0; i < g[u].size(); i++) {
int v = g[u][i];
if (cnt[{u, v}]) {
cnt[{u, v}]--; cnt[{v, u}]--;
dfs(v);
}
}
ans.push_back(u);
}
void Euler() {
for (int i = 1; i <= 500; i++) {
sort(g[i].begin(), g[i].end());
}
bool flag = 0;
for (int i = 1; i <= 500; i++) {
if (g[i].size() & 1) {
flag = 1; dfs(i);
break;
}
}
if (!flag) {
for (int i = 1; i <= 500; i++) {
if (g[i].size()) {
dfs(i);
break;
}
}
}
reverse(ans.begin(), ans.end());
}
编码问题的解
取所有 n − 1 n-1 n−1位数为节点,共 1 0 n − 1 10^{n-1} 10n−1个,每个节点有10条出边和入边,设当前节点为 a 1 a 2 . . . a n − 1 a_1a_2...a_{n-1} a1a2...an−1,那么它的第 r r r条出边连向节点 a 2 . . . a n − 1 r a_2...a_{n-1}r a2...an−1r,这样从一个节点顺着第 r r r条边走到另一个节点,就相当于输入了数字 x x x。
在节点对应的数的末尾加上某条出边的编号,就形成了一个 n n n位数,并且每个节点都能用这样的方式形成10个 n n n位数,共有 1 0 n 10^n 10n个 n n n位数对应所有密码,每条边映射一个密码。
下图是每位只有数字0,1的情况。
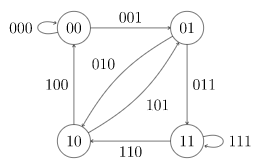
因此问题转化不重复地遍历所有边,即为求该图的欧拉回路,由于每个节点均有10条出边和10条入边,所以答案一定存在,这符合我们的认知,一定存在包含所有密码的数字串。