目录
算法分类:
问题描述
算法适用题目范围:
实现代码:
算法分类:
树状数组/线段树
问题描述
给定 n个数组成的一个数列,规定有两种操作,一是修改某个元素,二是求子数列 [a,b]的连续和。
输入格式
第一行包含两个整数 n 和 m,分别表示数的个数和操作次数。
第二行包含 n 个整数,表示完整数列。
接下来 m行,每行包含三个整数 k,a,b(k=0,表示求子数列[a,b]的和;k=1表示第 a个数加 b)。
数列从 1 开始计数。
输出格式
输出若干行数字,表示 k=0 时,对应的子数列 [a,b]的连续和。
数据范围
1≤n≤100000,
1≤m≤100000,
1≤a≤b≤n,
数据保证在任何时候,数列中所有元素之和均在 int 范围内。
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
输出样例:
11
30
35算法适用题目范围:
对于树状数组和线段树解决的问题:
1.单点修改
2.区间查询
具体细节见代码
树状数组和线段树的思路分析如下 来源:acwing蓝桥杯辅导课
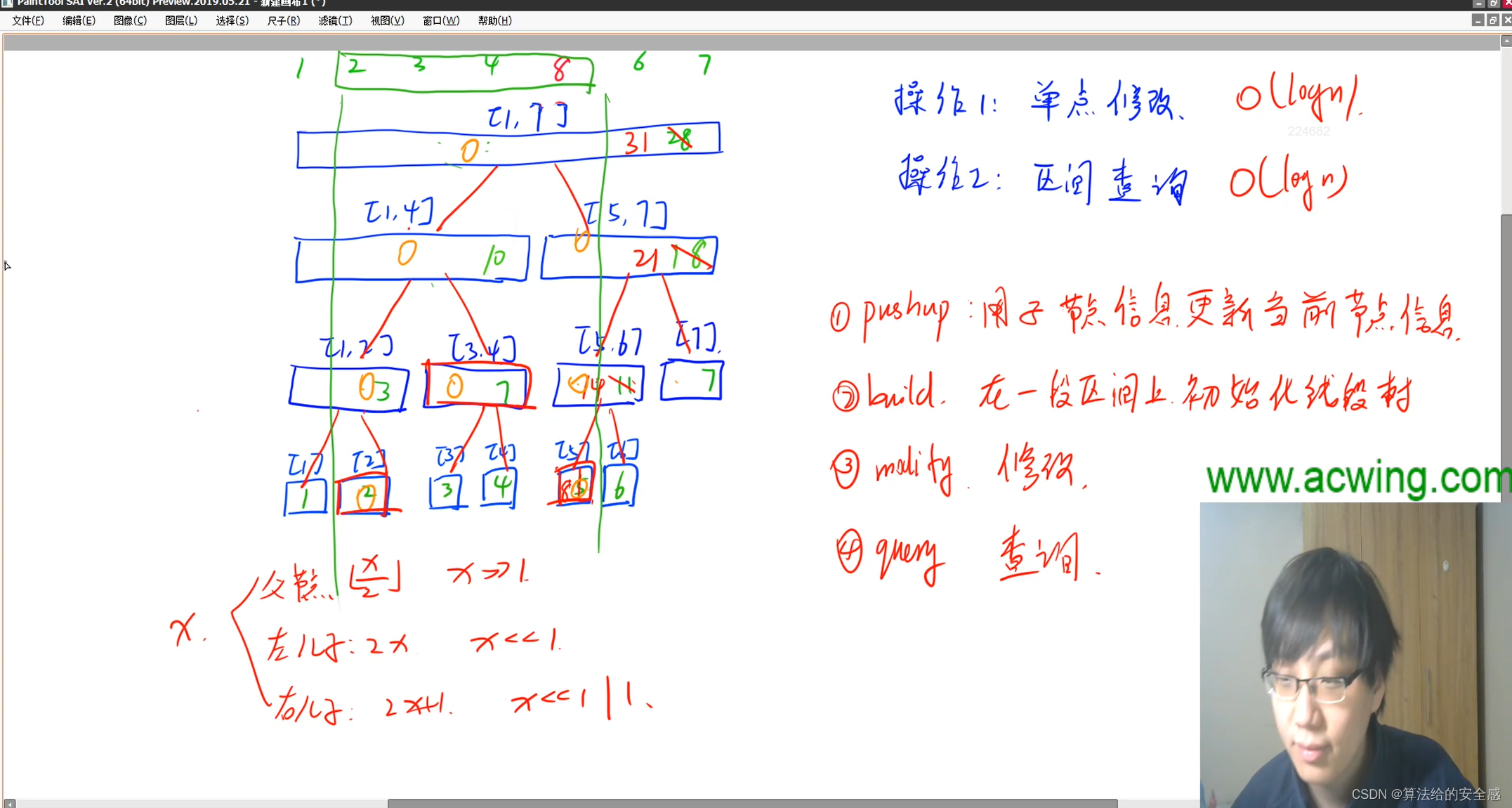
实现代码:
树状数组:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
int a[N];
int tr[N];
int n,m;
//返回2^k k为该数末尾连零的个数
int lowbit(int x){
return x&-x;
}
//单点修改
void add(int x,int v){
for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=v;
}
//区间查询 求前缀和
int query(int x){
int res = 0;
for(int i=x;i>0;i-=lowbit(i)) res+=tr[i];
return res;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
//初始化树状数组
for(int i=1;i<=n;i++) add(i,a[i]);
while(m--){
int k,x,y;
cin>>k>>x>>y;
if(k==0){
int res = 0;
res = query(y)-query(x-1);
cout<<res<<endl;
}
else{
add(x,y);
}
}
return 0;
}
线段树:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N = 1e5+10;
int n,m;
int w[N];//记录权值
struct Node{
int l,r,sum;
}tr[N*4];
void push_up(int u){
//一个节点为x
//父节点为x/2
//左儿子为x*2 x<<1
//右节点为x*2+1 x<<1|1
tr[u].sum = tr[u<<1].sum+tr[u<<1|1].sum;
}
//u为当前节点的编号 l左边界 r右边界
void build(int u,int l,int r){
//当前节点为叶节点
if(l==r) tr[u] = {l,r,w[r]};
else{
tr[u] = {l,r};
int mid = l + r >>1;
//递归左儿子
build(u<<1,l,mid);
//递归右儿子
build(u<<1|1,mid+1,r);
//更新一下当前节点的信息
push_up(u);
}
}
//查询函数 u为根节点的编号 l为查询的左边界 r为查询的有边界
int query(int u,int l,int r){
//当前节点被查询的区间包含在里面
if(l<=tr[u].l && tr[u].r<=r) return tr[u].sum;
//计算当前区间的中点
int mid = tr[u].l+tr[u].r>>1;
int sum = 0;//返回的结果
//判断左儿子所在的区间是否和查询区间有交集
if(mid>=l) sum+=query(u<<1,l,r);
//判断右儿子所在的区间是否和查询区间有交集
if(r>=mid+1) sum+=query(u<<1|1,l,r);
return sum;
}
//修改函数
//第一个参数也是当前的节点编号
//第二个参数为要修改的位置
//第三个参数为要修改的值 本题中是加多少
void modify(int u,int x,int v){
if(tr[u].l==tr[u].r) tr[u].sum+=v;
else{
int mid = tr[u].l+tr[u].r>>1;
//看一下x是在左边还是右边
if(x<=mid) modify(u<<1,x,v);
else modify(u<<1|1,x,v);
//记得要把当前的节点信息更新一遍
push_up(u);
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>w[i];
//初始化线段树 根节点编号为1 区间为1到n
build(1,1,n);
int k,a,b;
while(m--){
cin>>k>>a>>b;
//查询操作
if(k==0){
int sum = 0;
sum = query(1,a,b);
cout<<sum<<endl;
}
else modify(1,a,b);
}
return 0;
}