matlab动画模拟三体问题，微分方程，动力学

介绍

三体问题（Three-Body Problem）是经典力学中的一个著名问题，它研究的是三个质量相似的天体在相互引力作用下的运动规律。这个问题最早由艾萨克·牛顿（Isaac Newton）在1687年的《自然哲学的数学原理》中提出，随后在数学和物理学中成为一个重要的研究课题

三体问题的起源与基本定义

三体问题可以简单地定义为：在相互引力作用下，三个天体如何运动？每个天体对其他两个天体施加引力，同时也受其他两个天体的引力作用。由于引力是根据牛顿万有引力定律计算的，因此每个天体的加速度与其他天体的质量和距离有关。这使得三体问题成为一个高度非线性和复杂的动力学系统。

在数学上，三体问题的运动方程组如下：
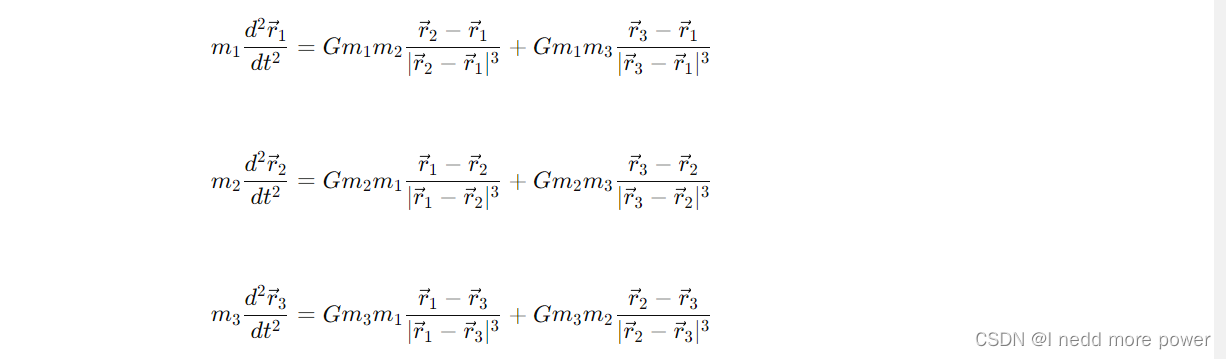
在这里插入图片描述
其中，𝑟⃗1,𝑟⃗2,𝑟⃗3分别是三个天体的位置向量，𝑚1,𝑚2,𝑚3是三个天体的质量，𝐺 是万有引力常数。

历史背景与研究进展

1.牛顿时代
牛顿在《自然哲学的数学原理》中提出了万有引力定律，并成功地解释了两体问题。然而，他也意识到三体问题的复杂性，无法通过解析解得出其普遍解答。

2. 拉普拉斯和拉格朗日
18世纪，拉普拉斯（Pierre-Simon Laplace）和拉格朗日（Joseph-Louis Lagrange）对三体问题进行了深入研究，发展了许多近似方法和特例解。例如，拉格朗日发现了三体问题的一个特殊解，即拉格朗日点，在这个解中，三个天体形成一个等边三角形并共同旋转。

3. 庞加莱的贡献
19世纪末，法国数学家亨利·庞加莱（Henri Poincaré）对三体问题进行了革命性的研究。他证明了三体问题没有一般的解析解，并首次提出了混沌理论的概念。庞加莱的工作揭示了三体问题的轨道可以是非常复杂和敏感的，对初始条件的微小变化会导致轨道的显著差异

三体问题的特性

1.混沌性
三体问题是混沌系统的经典例子。混沌性意味着系统对初始条件极其敏感，即微小的初始误差会随着时间的推移迅速放大。这使得长期预测三体系统的行为变得非常困难。

2. 复杂的轨道结构
三体问题的轨道可以呈现出非常复杂和多样的形态，从周期轨道到非周期轨道，从稳定轨道到混沌轨道。这种复杂性源于天体之间的非线性引力相互作用。

3. 特殊解和周期解
尽管三体问题没有一般的解析解，但存在一些特殊解和周期解。例如，拉格朗日点解是其中一个著名的特例。此外，还有一些周期性轨道，如八字形轨道和花形轨道，这些轨道在特定条件下可以保持稳定。

数值模拟与现代研究

1.数值方法
由于三体问题无法通过解析方法完全解决，数值模拟成为研究三体问题的主要手段。现代计算机技术的发展使得我们能够对三体系统进行高精度的数值积分，从而研究其长期动力学行为。

2. 分形与混沌
分形几何和混沌理论是现代三体问题研究的重要工具。通过数值模拟，研究者发现了三体问题轨道的分形结构，这些结构展示了轨道在相空间中的复杂分布。

3. 天文学中的应用
三体问题在天文学中有重要应用。例如，三体问题可以用来研究星系中的恒星动力学、行星系统的稳定性和双星系统的演化。此外，三体问题还可以帮助解释一些天文现象，如恒星的潮汐效应和引力波的产生。

三体问题的广义推广

1. 多体问题
三体问题是多体问题的一个特例。多体问题研究的是多个天体在相互引力作用下的运动。随着天体数量的增加，系统的复杂性和混沌性也随之增加，多体问题成为一个更具挑战性的研究领域。

2. 广义相对论下的三体问题
在广义相对论框架下，三体问题变得更加复杂。广义相对论考虑了时空的弯曲和引力波的传播，这对天体的运动产生重要影响。研究广义相对论下的三体问题可以帮助我们更好地理解引力和时空的本质。

3. 量子力学中的三体问题
在微观尺度上，三体问题也存在于量子力学中。例如，氦原子中的三个粒子（两个电子和一个原子核）构成一个三体系统。量子力学中的三体问题需要通过量子力学方程（如薛定谔方程）来描述，这为研究微观世界的相互作用提供了重要的理论基础。

三体问题在科学和文化中的影响

1. 文学与科幻
刘慈欣的科幻小说《三体》将三体问题引入了大众文化。这部小说通过虚构的三体世界，探讨了文明、科学和宇宙的深刻主题，引起了广泛的关注和讨论。

2. 教育与科普
三体问题作为经典力学中的一个重要课题，经常出现在物理学和数学的教育中。通过学习三体问题，学生可以了解动力系统的复杂性和混沌理论的基本概念，这对于培养科学思维和研究能力具有重要意义。

3. 科学研究与技术应用
三体问题的研究不仅在理论物理和天文学中具有重要意义，还在计算科学、数值模拟和复杂系统研究中发挥着关键作用。通过研究三体问题，科学家可以开发新的算法和技术，推动科学和技术的发展。

未来研究方向

1. 高精度数值模拟
随着计算机性能的提升，研究者可以进行更高精度和更长时间尺度的数值模拟，从而更深入地理解三体系统的长期行为和混沌特性。

2. 新的解析和近似方法
尽管三体问题没有普遍的解析解，但研究者依然在探索新的解析和近似方法，以期找到更多的特殊解和周期解。

3. 多体问题的推广
研究多体问题的推广，包括不同维度下的多体问题、不同相互作用形式下的多体问题，以及多体系统中的集体行为和相变现象

本文代码介绍

我们绘制三个天体，然后实时更新天体位置，描绘天体轨迹路线，来演示三体问题

核心代码

function animate_three_body_problem()
    % 时间范围
    tspan = [0, 50];
    
    % 初始条件 [x1 y1 z1 vx1 vy1 vz1 x2 y2 z2 vx2 vy2 vz2 x3 y3 z3 vx3 vy3 vz3]
    % 初始位置和速度
    y0 = [1 0 0 0 0.5 0; 
          -0.5 sqrt(3)/2 0 0 -0.5 0;
          -0.5 -sqrt(3)/2 0 0 -0.5 0];
    y0 = y0(:); % 展开为列向量
    
    % 使用ode45求解微分方程
    options = odeset('RelTol',1e-9,'AbsTol',1e-9);
    [t, y] = ode45(@three_body_equations, tspan, y0, options);
    
    % 提取每个天体的位置
    r1 = y(:, 1:3);
    r2 = y(:, 7:9);
    r3 = y(:, 13:15);
    
    % 创建一个figure窗口
    figure;
    hold on;
    grid on;
    axis equal;
    xlabel('X');
    ylabel('Y');
    zlabel('Z');
    title('Three-Body Problem Dynamic Simulation');
    
    % 预绘制轨迹线
    h1 = plot3(r1(1,1), r1(1,2), r1(1,3), 'r', 'LineWidth', 1.5);
    h2 = plot3(r2(1,1), r2(1,2), r2(1,3), 'g', 'LineWidth', 1.5);
    h3 = plot3(r3(1,1), r3(1,2), r3(1,3), 'b', 'LineWidth', 1.5);
    
    % 动态显示天体的位置
    scatter1 = plot3(r1(1,1), r1(1,2), r1(1,3), 'ro', 'MarkerFaceColor', 'r');
    scatter2 = plot3(r2(1,1), r2(1,2), r2(1,3), 'go', 'MarkerFaceColor', 'g');
    scatter3 = plot3(r3(1,1), r3(1,2), r3(1,3), 'bo', 'MarkerFaceColor', 'b');
    
    % 动画循环
    for i = 2:length(t)
        % 更新位置数据
        set(h1, 'XData', r1(1:i, 1), 'YData', r1(1:i, 2), 'ZData', r1(1:i, 3));
        set(h2, 'XData', r2(1:i, 1), 'YData', r2(1:i, 2), 'ZData', r2(1:i, 3));
        set(h3, 'XData', r3(1:i, 1), 'YData', r3(1:i, 2), 'ZData', r3(1:i, 3));
        
        drawnow;
    end
end

function dydt = three_body_equations(~, y)
    % 常量
    G = 1; % 万有引力常数，简化为1
    
    % 提取位置和速度
    r1 = y(1:3); v1 = y(4:6);
    r2 = y(7:9); v2 = y(10:12);
    r3 = y(13:15); v3 = y(16:18);
    
    % 计算相对位置
    r12 = r2 - r1; r13 = r3 - r1; r23 = r3 - r2;
    
    % 计算距离的平方和立方
    r12_norm = norm(r12); r13_norm = norm(r13); r23_norm = norm(r23);
    r12_norm3 = r12_norm^3; r13_norm3 = r13_norm^3; r23_norm3 = r23_norm^3;
    
    % 计算加速度
    a1 = G * (r12 / r12_norm3 + r13 / r13_norm3);
    a2 = G * (-r12 / r12_norm3 + r23 / r23_norm3);
    a3 = G * (-r13 / r13_norm3 - r23 / r23_norm3);
    
    % 组合导数
    dydt = [v1; a1; v2; a2; v3; a3];
end

说明

初始条件： y0 定义了三个天体的初始位置和速度。此例中，初始位置和速度根据等边三角形对称性条件设定。
求解微分方程：使用 ode45 函数求解常微分方程。odeset 函数用于设置求解精度。
提取位置：从求解结果中提取每个天体的位置数据。
预绘制轨迹线：使用 plot3 函数预先绘制出三个天体的轨迹线。
动态显示位置和轨迹：使用 plot3 函数动态显示每个天体的位置，并通过动画循环不断更新其位置。