Web墨卡托投影的原理和公式推导

简介

Web墨卡托投影(Web Mercator，EPSG:3857)是一种广泛应用于互联网地图的投影系统。Google地图、天地图等互联网地图通常情况下默认支持两种坐标系统，其一是WGS84地理坐标系，EPSG代码为4326，坐标形式为经纬度，另一种即为以WGS84地理坐标系为基础的墨卡托投影坐标

Web墨卡托投影的WKT表达式如下：

PROJCRS["WGS 84 / Pseudo-Mercator",
    BASEGEOGCRS["WGS 84",
        ENSEMBLE["World Geodetic System 1984 ensemble",
            MEMBER["World Geodetic System 1984 (Transit)"],
            MEMBER["World Geodetic System 1984 (G730)"],
            MEMBER["World Geodetic System 1984 (G873)"],
            MEMBER["World Geodetic System 1984 (G1150)"],
            MEMBER["World Geodetic System 1984 (G1674)"],
            MEMBER["World Geodetic System 1984 (G1762)"],
            MEMBER["World Geodetic System 1984 (G2139)"],
            ELLIPSOID["WGS 84",6378137,298.257223563,
                LENGTHUNIT["metre",1]],
            ENSEMBLEACCURACY[2.0]],
        PRIMEM["Greenwich",0,
            ANGLEUNIT["degree",0.0174532925199433]],
        ID["EPSG",4326]],
    CONVERSION["Popular Visualisation Pseudo-Mercator",
        METHOD["Popular Visualisation Pseudo Mercator",
            ID["EPSG",1024]],
        PARAMETER["Latitude of natural origin",0,
            ANGLEUNIT["degree",0.0174532925199433],
            ID["EPSG",8801]],
        PARAMETER["Longitude of natural origin",0,
            ANGLEUNIT["degree",0.0174532925199433],
            ID["EPSG",8802]],
        PARAMETER["False easting",0,
            LENGTHUNIT["metre",1],
            ID["EPSG",8806]],
        PARAMETER["False northing",0,
            LENGTHUNIT["metre",1],
            ID["EPSG",8807]]],
    CS[Cartesian,2],
        AXIS["easting (X)",east,
            ORDER[1],
            LENGTHUNIT["metre",1]],
        AXIS["northing (Y)",north,
            ORDER[2],
            LENGTHUNIT["metre",1]],
    USAGE[
        SCOPE["Web mapping and visualisation."],
        AREA["World between 85.06°S and 85.06°N."],
        BBOX[-85.06,-180,85.06,180]],
    ID["EPSG",3857]]

proj表达式如下：

+proj=merc +a=6378137 +b=6378137 +lat_ts=0 +lon_0=0 +x_0=0 +y_0=0 +k=1 +units=m +nadgrids=@null +wktext +no_defs

投影特点

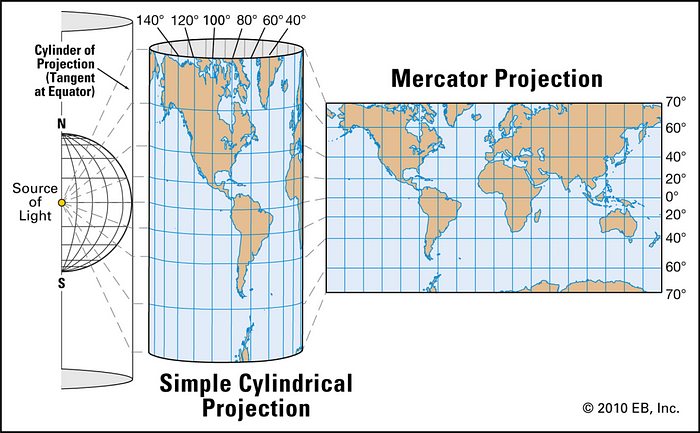
如下图所示，从投影方式来看，Web墨卡托投影属于正轴等角切圆柱投影，该投影方式将投影圆柱竖直放置，使其圆周外轮廓与地球参考球体的赤道相切，此时从参考球体的中心发出投影射线，将地球参考球体投影在圆柱体侧立面上，再将该投影圆柱侧面展开，即得到Web墨卡托投影平面。

Web墨卡托投影坐标系的x轴与参考球体的赤道重合，从经度-180°指向180°，y轴与0°经线重合，从纬度-90°指向90°

正如前述所说，Web墨卡托投影以WGS84地理坐标系为基础，该地理坐标系的基准平面为椭球体，但是Web墨卡托投影在进行投影公式推导时将该参考椭球体近似为一个标准球体，这是该投影坐标系的主要不足之一。

投影公式推导

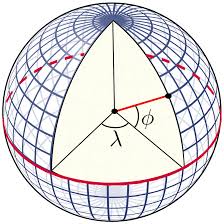
从纬线圈来看，基于正轴等角切圆柱投影的特点，Web墨卡托投影会将所有的纬线圈投影为大小相同的圆环，该圆环即为投影圆柱的圆周。由于投影圆柱与地球参考球体在赤道处相切，且投影中心与参考球体中心重合，因此赤道处的纬线圈的投影变形为1。假设地球参考球体的半径为$R$，其它纬度为$\varphi$的纬度圈，在投影前的周长$C_1=2\pi R\cos (\varphi )$，在投影后的周长$C_2=2\pi R$，因此纬线圈的投影变形为$C_2/C_1=1/\cos (\varphi )$，由此可得维度越高，纬线圈即投影坐标系中x轴方向的投影变形越大

投影点的x轴坐标的计算公式如下：
$$x=\lambda \cdot R\cos (\varphi )\cdot 1/\cos (\varphi )=\lambda \cdot R$$
从经线圈来看，由于Web墨卡托投影属于等角投影，即投影前后方向角度保持不变，投影前后的图形具有相似关系，因此经线圈（y轴方向）的投影变形需要和纬线圈（x轴方向）保持一致，因此Web墨卡托投影的投影变形与经度维度，只与维度有关，为$1/\cos (\varphi )$

经线圈不同位置的投影变形随着纬度的变化而不同，因此需要通过积分来计算投影点y轴的坐标，公式如下：
$$d\varphi \cdot R\cdot 1/\cos (\varphi )=dy$$

$${\int }_0^{\varphi }R/\cos (\varphi )d\varphi ={\int }_0^{y}dy$$

$$y=R\cdot \ln [\tan (\frac{\pi }{4}+\frac{\varphi }{2})]$$

由投影坐标下(x,y)反算经纬度的公式如下：
$$\lambda =\frac{x}{R}$$

$$\varphi =2\cdot \arctan (e^{\frac{y}{R}})-\pi /2$$

从投影坐标正算公式可知，当纬度为±90°时，此时y的投影坐标为$\pm \infty$，然而在实际处理中，一般将参考球体投影到一个正方形平面，此时
$$y_{max}=x_{max}={\lambda }_{max}\cdot R=\pi \cdot R$$
反算此时纬度范围
$${\varphi }_{max}=2\cdot \arctan (e^{\frac{\pi \cdot R}{R}})-\frac{\pi }{2}=1.484rad=85.051^{°}$$
$${\varphi }_{min}=2\cdot \arctan (e^{\frac{-\pi \cdot R}{R}})-\frac{\pi }{2}=-1.484rad=-85.051^{°}$$

转换代码

// 经纬度转Web墨卡托坐标
const lonlatToxy = (lon, lat) => {
	const x = (lon / 180) * Math.PI * EARTHRADIUS;
	const y =
		Math.log(Math.tan(Math.PI / 4 + ((lat / 180) * Math.PI) / 2)) *
		EARTHRADIUS;
	return [x, y];
};
// web墨卡托坐标转经纬度坐标
const xyTolonlat = (x, y) => {
	const lon = x / EARTHRADIUS / Math.PI * 180;
	const lat = (2 * Math.atan(Math.exp(y / EARTHRADIUS)) - Math.PI / 2) / Math.PI * 180;
	return [lon, lat];
};