加减法运算是计算机中最基本的计算，由于减法可以看成是负值是加法，因此计算机中使用补码表示有符号数之后，可以将减法运算和加法运算合并在一起讨论。

1.补码的加减运算

补码加减运算的规则简单，公式如下(设机器字长为n)：

补码运算的特点如下：

1.逢2进1

2.如果做加法，两数的补码直接相加；如果做减法，则将被减数加上减数的机器负数。

3.符号位和数值位一起参与运算，加、减运算结果的符号位也在运算中直接得出。

4.最终将运算结果的超过n位的位丢弃，保留n位，运算结果也是补码。

假设机器字长位8，那么

2.溢出判别方法 

溢出是指运算结果超过了数的表示范围。通常，大于能表示的最大正数称为正上溢，小于能表示的最小负数称为负下溢。

 补码加减运算的溢出判断方法有两种：

（1）采用一位符号位

由于减法运算在机器中是用加法器实现的，减法可以看作一个正数和负数的加法；所以不管是加法还是减法，只要参加操作的两个数符号位相同，但是结果又与原操作数不同，则表示结果溢出。

但是一正一副相加必然不会溢出。

（2）采用双符号位

运算结果的两个符号位相同则表示未溢出，若两个符号位不同则溢出。

若发生了溢出，则此时的最高位就代表真正的符号。但是由于溢出了，我们要把它丢掉。

符号位为00表示正数无溢出 为11表示负数无溢出，

           为01表示结果正溢出 为10表示结果负溢出。

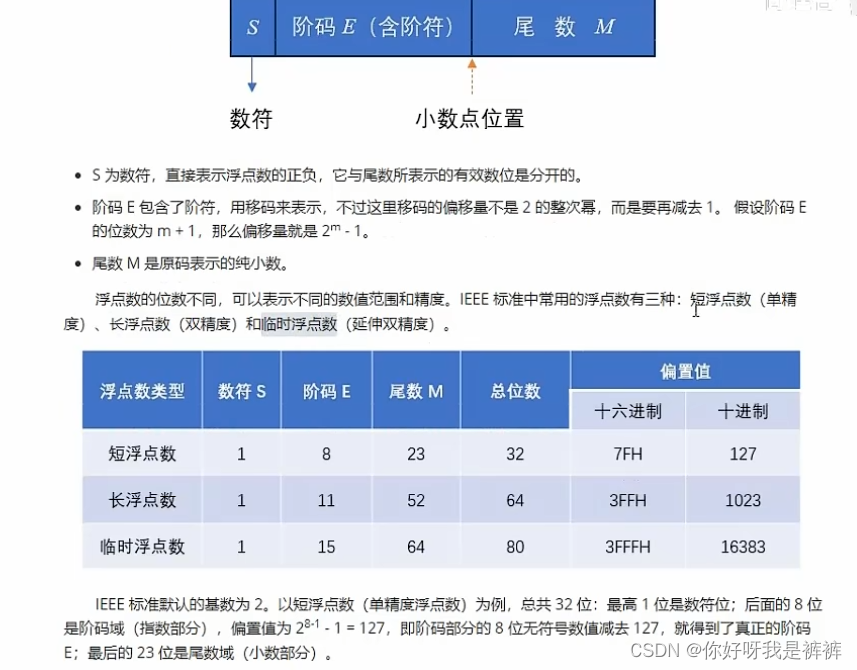
2.浮点数的表示

浮点数是小数点可以浮动的数。例如：

 3.浮点数的表示范围

很明显，采用补码的优势在于方便做加减运算，但是在表示尾数时，数值范围就无法相对远点对称了。而且对于浮点数来说，尾数是不能直接做加减的，因此需要先把阶数对齐，所以使用补码的好处并不明显；反而是在做乘除运算时，阶码需要直接做加减操作。

所以我们可以发现，阶码可以用补码表示，而尾数用原码和补码表示都可以，而原码会更好一些。

用移码表示阶码还有一个好处，就是方便进行对阶（阶数的比较和对齐） 

4.浮点数的规格化

由于规格化数的精度最高，所以一个非零的浮点数不是规格化数时，应该通过左右移动尾数、并同时修改阶码的方法，将它转换为规格化数。把一个非规格化数转换成规格化数的过程，叫做规格化。

规格化的本质类似于科学计数法的表达，通过保证尾数的最高数位上是一个有效值，尽可能多地保留有效数字的尾数，从而提高精度。

规格化可以分为左规和右规两种。

以基数r=2为例：

左规：

• 向左规格化，当运算结果尾数的最高有效位不是有效位，即出现0.00......01...的形式时，需要向左规格化。
• 左规时，尾数左移一位，阶码减1；

右规：

• 向右规格化，当运算结果尾数的小数点左侧出现有效位，即整数部分不为0时，需要向右规格化。右规时，尾数右移动一位，阶码+1
• 需要右规时，只需要规1次。

---------------------------------------------------------------------------------------------------------------------------------当基数不为2时，比如基数为4，阶码每次加/减1，就相当于多乘/除以4，也就是左/右移两位。

我们规定尾数两位不全为0的数，就是规格化数。

规格化数的取值范围缩小了，下图是规格化数的取值范围。

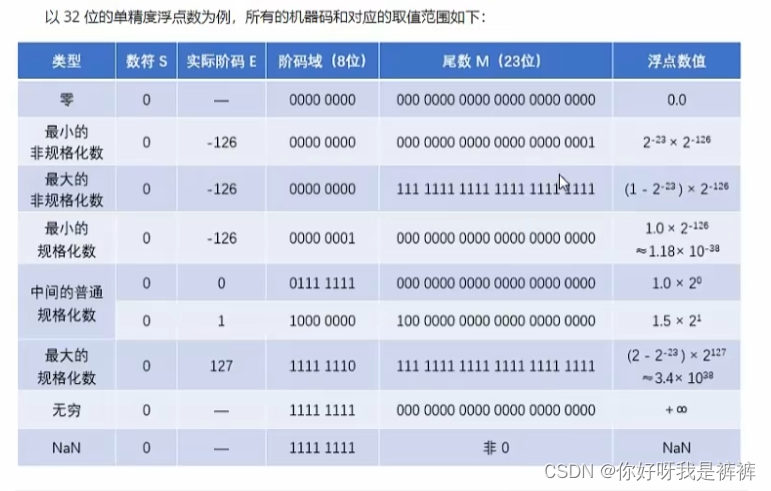
5.IEEE 754标准

• IEEE标准用规格化数表示一般的数值，这时尾数M的最高有效位一定为1；于是IEEE标准规定这个最高有效位的1可以省略，并且将它隐藏放在整数位上，称为“隐藏位”。这样就可以多出一位有效数位，从而提高了精度。就比如：短浮点数的23位尾数，可以表示24位有效数字。临时浮点数不采用隐藏位的方案。
• IEEE标准使用非规格化数表示0附近的很小的数。这时阶码E所有位全部位0；尾数M不为0，且没有隐藏位。或者说隐藏位为0.

此外，IEEE标准还规定了几种特殊情况：

• 阶码E所有位为0，并且尾数M也为0.表示0 。根据数符不同可分为正负0
• 阶码E所有位全为1，并且尾数M为0时，表示无穷大，也可以分为正负无穷
  • 阶码E所有位为1，并且M不为0时，表示这不是一个数（NaN-->Not a Number）。

非规格化数中，阶码减去偏执量之后要加1，这样可以让它跟最小的规格化数有一个平滑的过渡。

原因是：最小的规格化数减去最小的非规格化数便是最大的非规格化数，而最小的非规格化数是非常小的。

 6.定点、浮点的区别

• 数值的表示范围不同。对于相同的字长，浮点表示法所能表示的数值范围远大于顶点表示法。
• 数值精度不同。对于相同的字长，浮点数虽然扩大了数的表示范围，但精度降低了（可用于表示数的位少了）
• 数据的运算不同。浮点数需要算阶码和尾数量部分，而且还需要考虑规格化。
• 溢出的定义不同，定点数运算中，只要运算结果超出了数的表示范围则溢出。而浮点数运算中，当运算结果超出尾数表示范围后，不一定发生溢出；只有规格化后，阶码超出所能表示的范围时，才发生溢出。

7.浮点数的运算

（1）对阶

“小阶向大阶看齐”，将阶码小的尾数右移一位（r=2），阶码加1，直到两个数的阶码相等。

（2）尾数求和

对尾数求和

（3）规格化

需要注意，右规时，最高位1被移到小数点前一位时，作为隐藏位即可；当最后一位移出时，要考虑舍入。

（4）舍入

在对阶和尾数右规时，右移可能会让低位丢失，影响精度，IEEE 754有以下四种舍入方式：

1. 就近舍入-->类似于四舍五入
2. 正向舍入-->取右边的数，也叫“向上舍入”
3. 负向舍入-->取左边的数，也叫“向下舍入”
4. 截断->像0方向舍入，即取绝对值较小的那个值。

（5）溢出判断

浮点数的溢出并不是以尾数溢出来判断的；尾数溢出可以通过右规操作来纠正。运算结果是否溢出看的是阶码。

• 上溢-->异常
• 下溢-->把结果当机器零处理。