一．实验目的

1、理解模拟信号数字化的原理；
2、理解抽样过程，掌握抽样定理；
3、理解由抽样序列恢复信号。

二、实验内容

设低通信号为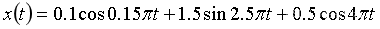在这里插入图片描述

1、画出该低通信号的波形；
2、画出抽样速率为4Hz的抽样序列；
3、由抽样序列恢复出的信号。

三、实验原理

1.模拟信号数字过程
模拟信号通过抽样、量化、编码过程转变为数字码元序列。
第一步抽样。模拟信号被抽样后,成为抽样信号,它在时间上是离散的,但是其取值仍然是连续的,所以是离散模拟信号。
第二步是量化。量化使信号变成量化信号，其取值是离散的故量化信号已经是数字信号了，它可以看成是多进制的数字脉冲信号调制。
第三步是编码。将量化信号二进制化，最基本和最常用的编码方法是脉冲编码。

2.抽样定理
低通抽样定理：一个频带限制在(0，fH)内的低通信号m(t)，如果以fs≥2fH的速率进行均匀抽样，则由抽样序列{m(nTs)}可无失真地恢复出m(t)，其中2fH被称为奈奎斯特抽样速率，也是最小抽样速率。
即想要采样后能够不失真地还原出原信号，则采样信号必须大于信号最高频率的两倍
时域上看时域采样就是让信号与采样信号进行卷积，而采样信号是一串冲击序列，
从频域上看就是原信号向冲击脉冲脉冲所在的位置的平移，即频谱搬迁，采样后后信号的频谱公式：
频谱搬迁这个结论说明了输出信号是原信号频谱以采样频率为重复周期的频域延拓，那就会存在一个问题，不同的采样频率采的出来的频谱不一样，有些稀疏，有些密集，当密集到一定程度就会出现混叠，那样我们就不能通过一个滤波器把原信号的频谱给滤出来，进而采样过程变成了不可逆过程，频域图可以看出了原信号的最高频率是WH，相邻两个频谱相切时中心频率相差WS，要不混叠即要满足WS≥2WH。
抽样过程在时域和频域的示意图：

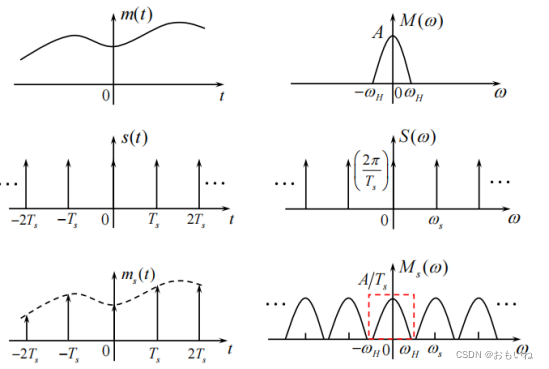
3.采样恢复
采样恢复，也就是将离散时间信号变回连续时间信号。
由采样可知，采样后的频谱是原频谱的复制粘贴，我们只需要通过一个理想低通滤波器，那么就可以得到原信号的频谱。在恢复原信号时，抽样时刻的值由抽样值确定，而抽样时刻之外的信号值则是无穷项内插函数的加权和。
根据以上分析，我们需要一个如以下的低通滤波器进行信号的恢复。
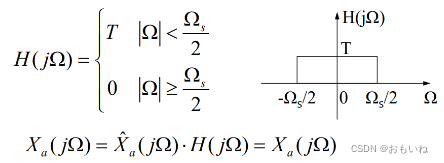
在这里插入图片描述
根据上面频域相乘可知恢复信号等于抽样信号与低通滤波器的冲激响应做卷积.我们得到了时域中恢复信号的表达式
恢复信号的表达式也说明了，只要抽样频率大于两倍信号最高频率，则原信号的整个频谱就会完整保留下来，从而整个连续信号时间信号就可以完全由它的抽样值代表，而不会丢失任何信息，这也是奈奎斯特采样定理的意义。

四、实验程序

%参数设定
t=-5:0.05:5;%信号长度
f1 = 5;
f2 = 10;
k = -1 : 0.0001 : 1;
W = k / 0.01 ; %频域范围
%原信号
f_origin =  0.1*cos(0.15*pi*t) + 1.5*sin(2.5*pi*t)+0.5*cos(4*pi*t);
F_origin = f_origin * exp(-1i * t' * W) * 0.0005;% F_origin = abs(F_origin);
%4hz采样
fs = 4;
Ts = 1 / fs;
n = -5 : 1/fs : 5;%采样点
f_4Hz =0.1*cos(0.15*pi*n) + 1.5*sin(2.5*pi*n)+0.5*cos(4*pi*n);
F_4Hz = f_4Hz * exp(-1i * n' * W) * Ts;
F_4Hz = abs(F_4Hz);
%4Hz恢复
y = f_4Hz * sinc((ones(length(n),1)*t - n'*ones(1,length(t))) * fs);
F_Y = y * exp(-1i * t' * W) * Ts; 
F_Y = abs(F_Y);
figure(1)
subplot(311);plot(t, f_origin);title('原信号');
subplot(312);stem(n,f_4Hz);title('4hz采样信号');
subplot(313);plot(t,y);title('恢复后信号');
figure(2)
subplot(311);plot(W , F_origin);title('原始信号频谱');
subplot(312);plot(W,F_4Hz);title('4hz采样信号频谱');
subplot(313);plot(W,F_Y);title('恢复信号的频谱');

五、实验结果与分析

原始信号、抽样序列、以及恢复信号的波形如下：
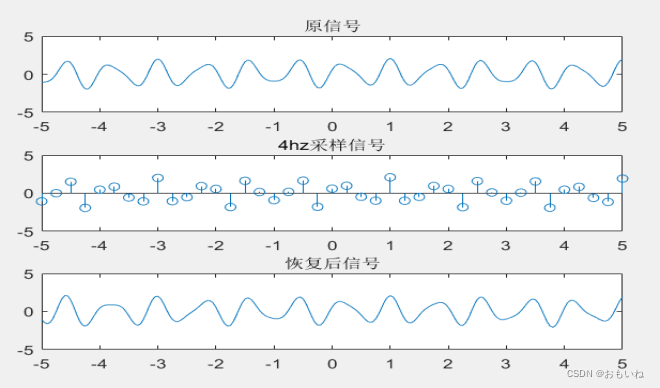
可以看出抽样序列经过一定处理，可以恢复到原信号。
2.原始信号、抽样序列、以及恢复信号的频谱如下：
如下图所示，当采样频率为4Hz，正好为原信号最高频率的二倍，也就是奈奎斯特抽样速率，满族抽样定理。由图可知，经采样后频谱并没有发生混叠，恢复信号过程中，经过一个低通滤波器，系统原信号的频谱被完整的恢复出来，实现了信号的恢复。

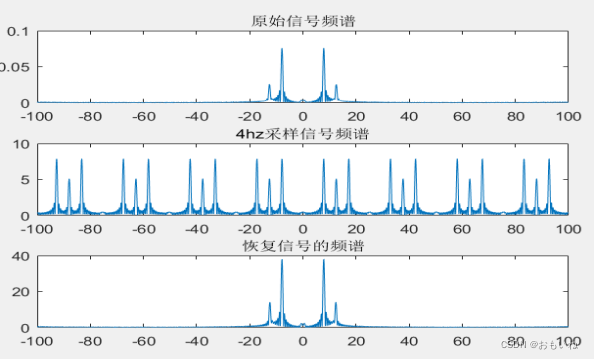
六、问题讨论

1.总结本实验的主要收获。
①掌握了使用maatlab进行采样，将采样序列恢复到原始信号的方法。
②对采样定理，以及如何恢复原信号有了更加深刻的理解和掌握。
③掌握了matlab中常见数学操作，对matlab编程更加的熟练。
2.对实验内容提出自己的想法和建议。
可以通过进一步改变采样频率，观察不同采样频率下的采样序列，恢复原信号的波形，以及频谱特性。