文章目录
- 课程前提知识
- 问题引入
- 模型改进
- 修改
- 神经层的增加
- 学习能力与超参数
- 课本代码
课程来源: 链接
课程文本来源借鉴: 链接
以及(强烈推荐)Birandaの
课程前提知识
BCELoss - Binary CrossEntropyLoss
BCELoss 是CrossEntropyLoss的一个特例,只用于二分类问题,而CrossEntropyLoss可以用于二分类,也可以用于多分类。
如果是二分类问题,建议BCELoss
问题引入
有一糖尿病数据集,在文件中,每个样例有8个维度的信息,并以此进行二分类。
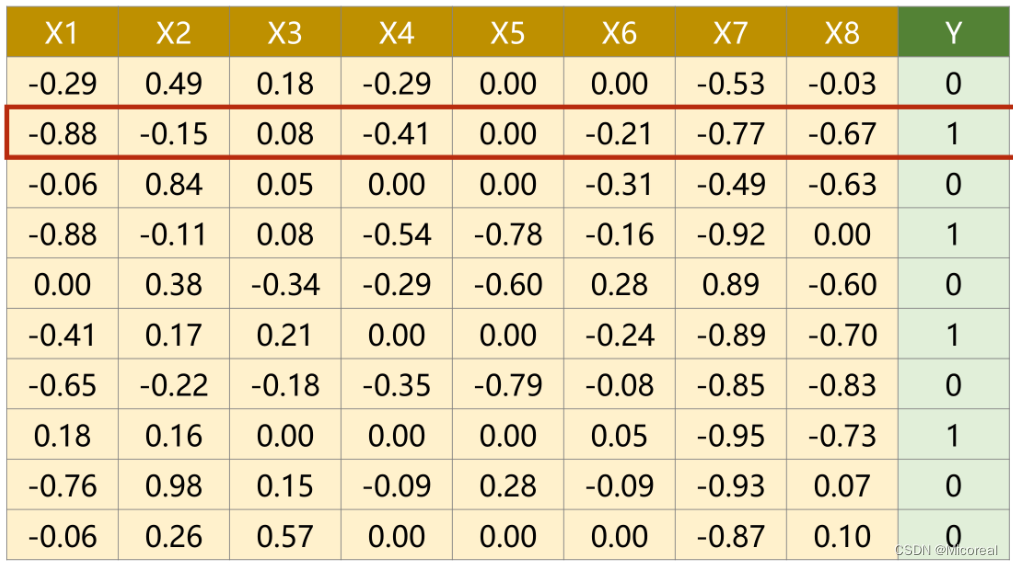
模型改进
上篇中,单维度逻辑回归模型为
y
^
(
i
)
=
σ
(
x
(
i
)
ω
+
b
)
\widehat y^{(i)} = \sigma(x^{(i)} \omega+b)
y
(i)=σ(x(i)ω+b)
其中的
x
(
i
)
x^{(i)}
x(i)表示第i个样本的维度,对于多维度,输入要变为8个维度的输入因此,模型应当变为
y
^
(
i
)
=
σ
(
∑
n
=
1
8
x
n
(
i
)
ω
n
+
b
)
\widehat y^{(i)} = \sigma(\sum _{n=1}^8 x^{(i)}_n \omega _n+b)
y
(i)=σ(n=1∑8xn(i)ωn+b)
其中的
x
n
(
i
)
x^{(i)}_n
xn(i)表示第i个样本的第n个维度。由于在实际代码运算中是以矩阵进行计算的,因此其中
∑
n
=
1
8
x
n
(
i
)
ω
n
=
[
x
1
(
i
)
⋯
x
8
(
i
)
]
[
w
1
⋮
w
8
]
\sum _{n=1}^8 x^{(i)}_n \omega _n = \begin{bmatrix} {x_1^{(i)}}&{\cdots}&{x_8^{(i)}} \end{bmatrix} \begin{bmatrix} {w_1}\\ {\vdots}\\ {w_8} \end{bmatrix}
n=1∑8xn(i)ωn=[x1(i)⋯x8(i)]
w1⋮w8
则原式可以表示成
y
^
(
i
)
=
σ
(
[
x
1
(
i
)
⋯
x
8
(
i
)
]
[
w
1
⋮
w
8
]
+
b
)
=
σ
(
z
(
i
)
)
\widehat y^{(i)} = \sigma( \begin{bmatrix} {x_1^{(i)}}&{\cdots}&{x_8^{(i)}} \end{bmatrix} \begin{bmatrix} {w_1}\\ {\vdots}\\ {w_8} \end{bmatrix}+b)\\ =\sigma(z^{(i)})
y
(i)=σ([x1(i)⋯x8(i)]
w1⋮w8
+b)=σ(z(i))
修改

神经层的增加
矩阵实质上是用于空间的函数

由此,也可以将输出的部分转换为其他维度,来实现分布的维度下降,比如8维转6维,6维转4维,4维转1维,由此可以增加网络层数,增加网络复杂度。同理,对网络结构先增后减也是可以的。
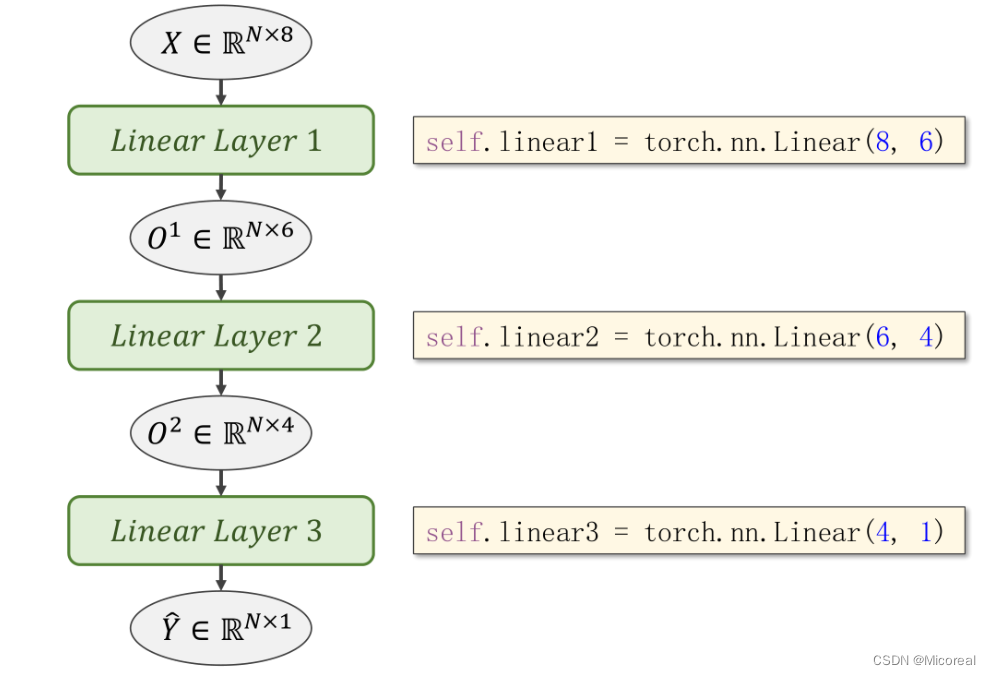
学习能力与超参数
层与层的叠加,就是多层神经网络。每层之间的矩阵大小选择,也是超参数的搜索问题
层数太多,学习能力太强,会把噪声的规律也学进来,而抓不住学习的重点。所以层数,每层的维度,是一个超参数搜索问题。
课本代码
import torch
import numpy as np
#读取文件,一般GPU只支持32位浮点数
xy = np.loadtxt('diabetes.csv', delimiter=',', dtype = np.float32)
#-1行-1列不取
x_data = torch.from_numpy(xy[:-1, :-1])
#单取-1列作为矩阵
y_data = torch.from_numpy(xy[:-1, [-1]])
#取-1行的测试集部分
test_data = torch.from_numpy(xy[[-1], :-1])
pred_test = torch.from_numpy(xy[[-1],[-1]])
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
return x
model = Model()
criterion = torch.nn.BCELoss(size_average=True)
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
for epoch in range(1000):
#Forward 并非mini-batch的设计,只是mini-batch的风格
y_pred = model(x_data)
loss = criterion(y_pred,y_data)
print(epoch, loss.item())
#Backward
optimizer.zero_grad()
loss.backward()
#Update
optimizer.step()
print("test_pred = ", model(test_data).item())
print("infact_pred = ", pred_test.item())
而值得关注的是使用relu激活函数的时候,在最后一层神经网络改成使用sigmoid,因为如果继续使用relu,可能会变成0