701.二叉搜索树中的插入操作
这道题较为简单,只需要通过递归找到符合要求的叶子节点,并将节点插入即可。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
//遇到节点为空,就返回一个val值的节点,相当于将该节点接到子节点的左子树或者右子树上
if(root == null) return new TreeNode(val);
//如果val小于root.val,说明应该往左边插入
if(val < root.val) root.left = insertIntoBST(root.left,val);
//如果val大于root.val,说明应该往右边插入
else root.right = insertIntoBST(root.right,val);
//返回完成操作之后的root即可
return root;
}
}
450.删除二叉搜索树中的节点
这道题就复杂得多,删除节点所涉及的情况有五种,因为遇到要删除的节点需要立马删除,所以将删除的操作体现在终止条件里,并返回删除之后的root节点。
删除的节点的五种可能性:
1.整个二叉数都没有key节点
2.key节点在叶子节点上
3.key节点的右节点不为空,左节点为空,返回root.left
4.key节点的左节点为空,右节点不为空,返回root.right
5.key节点的左右节点都为不为空,这种情况是最复杂的,需要先将key节点左子树接到右子树最小值的左边
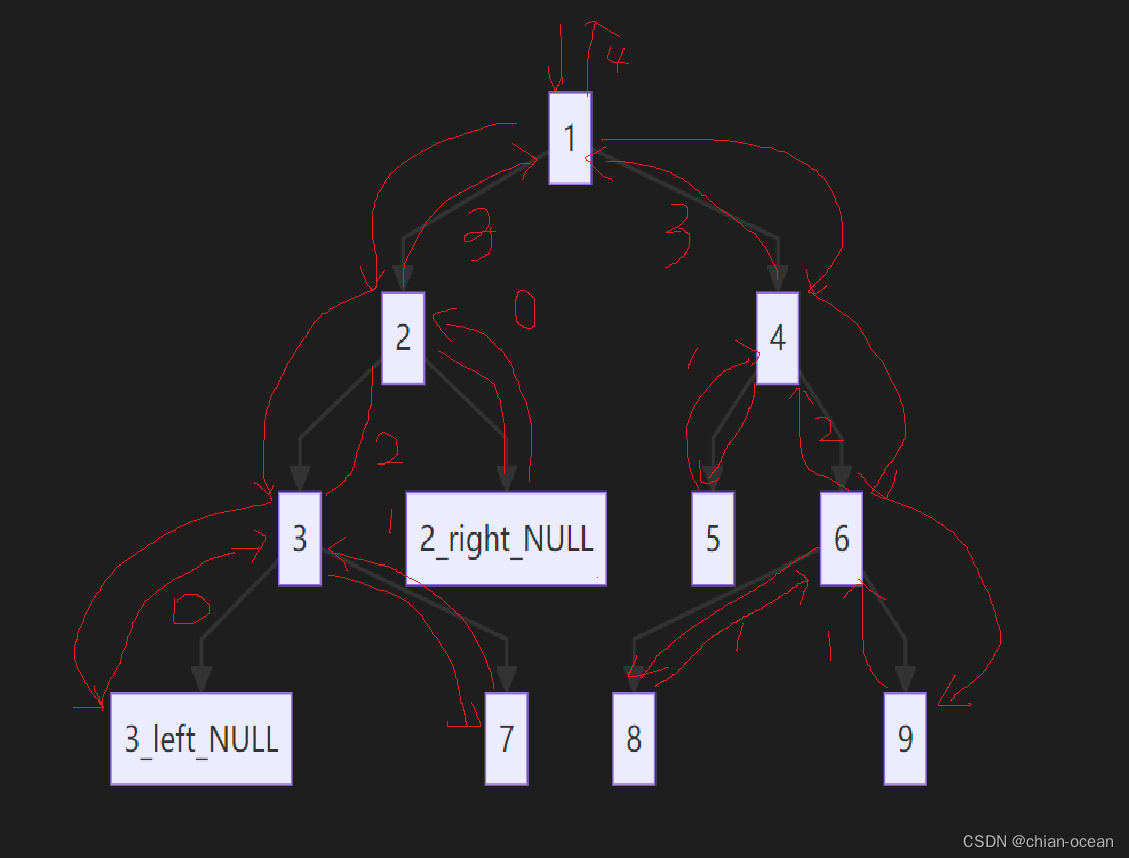
如下图所示,我们要删除的key为11,那么再删除之前,要将左子树处理一下。

将左子树拼接到右子树上那个比自己根节点大一点点的那个节点的左边,然后删除val=11的节点

最后得到了这个处理之后的二叉树

代码如下:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
//终止条件较为复杂,有五种不同的情况。并且key节点发现即要删除,因此删除的操作也包含在终止条件中
//情况一:没有找到key,返回null
if(root == null) return null;
//后四种情况属于找到key节点的这一前提下的子情况
if(root.val == key){
//情况二:找到的key为叶子结点,直接删除即可
//因为后面会用父节点的左子树去承接,因此返回null相当于删除
if(root.left == null && root.right == null) return null;
//情况三:左空右不为空
else if(root.left == null && root.right != null) return root.right;
//情况四:右空左不为空
else if(root.left != null && root.right == null) return root.left;
//情况五:左右均不为空
//需要先将左子树移到右子树中最小的节点的左子树上,以保证删除后符合平衡
TreeNode cur = root.right;
while(cur.left != null) cur = cur.left;
cur.left = root.left;
//将当前节点删除
return root.right;
}
//需要判断向哪一边去寻找要删除的key节点
if(key > root.val) root.right = deleteNode(root.right,key);
if(key < root.val) root.left = deleteNode(root.left,key);
return root;
}
}
235. 二叉搜索树的最近公共祖先
236. 二叉树的最近公共祖先
这两个题目可以用一套相同的解法,代码如下:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
//因为从下往上去处理,因此可以用左右中的后序遍历
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
return returnNode(root,p,q);
}
public TreeNode returnNode(TreeNode root, TreeNode p, TreeNode q){
//终止条件,遇到空或者q或者q就可以返回了
if(root == null) return null;//遇到空即返回
if(root.val == p.val || root.val == q.val) return root;//如果遇到p或者q,就返回root
//左
TreeNode leftNode = returnNode(root.left,p,q);
//右
TreeNode rightNode = returnNode(root.right,p,q);
//中
if(leftNode != null && rightNode != null) return root;
else if(leftNode == null && rightNode != null) return rightNode;
else if(leftNode != null && rightNode == null) return leftNode;
else return null;
}
}