目录
一、题目描述
二、解题思路
三、参考答案
一、题目描述
矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
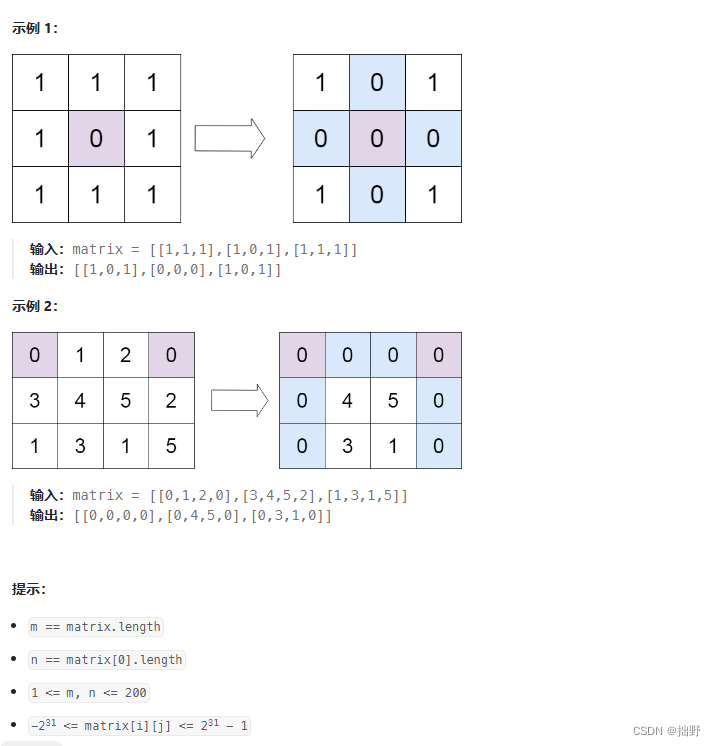
进阶:
- 一个直观的解决方案是使用
O(mn)的额外空间,但这并不是一个好的解决方案。 - 一个简单的改进方案是使用
O(m + n)的额外空间,但这仍然不是最好的解决方案。 - 你能想出一个仅使用常量空间的解决方案吗?
二、解题思路
我们可以创建两个布尔型标记数组,分别用来标记每一行和每一列中是否存在零元素。具体操作如下:首先遍历整个数组,当遇到元素值为0时,相应地将该元素所在的行和列在标记数组中的对应位置设为true。完成初步标记后,再次遍历原数组,利用之前设定的标记数组来更新原数组中的元素。这种方法能有效记录并处理零元素的位置。
三、参考答案
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
// 定义两个数组来标记该行列是否有0
boolean[] row = new boolean[m];
boolean[] col = new boolean[n];
// 遍历二位数组,设置行列数值的值
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 为0则所在行列标记为true
if (matrix[i][j] == 0)
row[i] = col[j] = true;
}
}
// 第二次遍历,根据标记数组的结果来更新原数组
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 当前遍历元素所在行列标记为true,则当前元素为0
if (row[i] || col[j])
matrix[i][j] = 0;
}
}
}
}以上其实就是使用标记数组的方法来解决矩阵置零问题。通过创建两个数组,分别记录需要置零的行和列,然后再次遍历矩阵进行置零操作,我们可以实现对原矩阵的修改。这种方法的时间复杂度为O(mn),空间复杂度为O(m+n)。其中m是矩阵的行数,n是矩阵的列数。
那么我们怎么能不借助额外空间,来达到空间复杂度为O(1)呢?
我们可以使用矩阵的第一行和第一列来代替方法一中的两个标记数组,以达到O(1)的额外空间。
但是如果第一行和第一列中就有0,该怎么办呢?
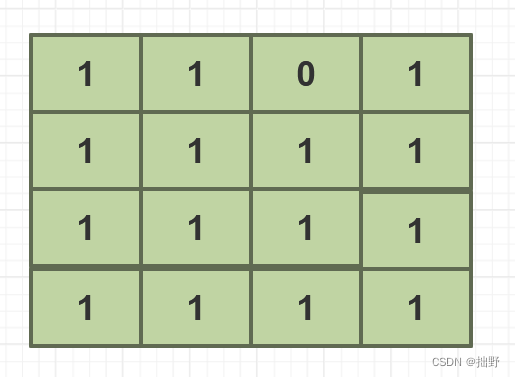
就比如上图矩阵,当我们遍历到[0,2]位置的时候,也就是第一行有0的位置的时候。我们用第一行第一列标记的时候,那么此时我们的操作就是matrix[0][0]=matrix[0][2] = 0。因为matrix[0][0] = 0,那么当我们根据第一行和第一列的值来对原数组置零的时候,最终结果就如下:
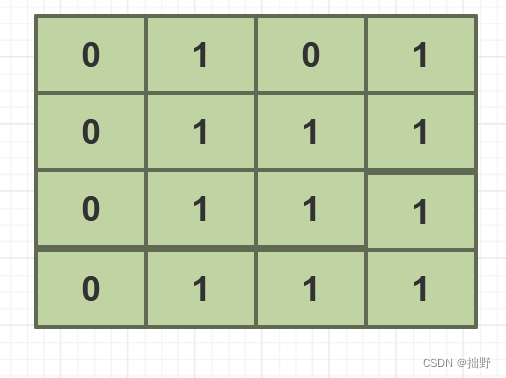
显然,这是不符合要求的。导致这个问题的原因就是第一行和第一列共用了matrix[0][0],当matrix[0][0]=0的时候,我们无法得知它是标记的行还是列,还是两者都进行了标记。所以,在置零原数组的时候,我们可以不置零第一行和第一列的元素。而是在第一次遍历进行标记的时候,另外使用两个变量来标记行列是否有0。如果有0,再单独进行行列的处理。
那么此时的代码就如下:
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
// 定义两个变量来标记该行列是否有0,默认false,没有零
boolean rowZero = false;
boolean colZero = false;
// 遍历二位数组,设置行列数值的值
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 为0则所在行列标记为true
if (matrix[i][j] == 0) {
matrix[i][0] = matrix[0][j] = 0;
// 如果是第一行,则标记该行是否有0的标记为true
if (i == 0)
rowZero = true;
// 如果是第一列,则标记该列是否有0的标记为true
if (j == 0)
colZero = true;
}
}
}
// 第二次遍历,根据标记结果来更新原数组
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][0] == 0 || matrix[0][j] == 0)
matrix[i][j] = 0;
}
}
// 处理第一行和第一列
for (int i = 0; colZero && i < m; i++)
matrix[i][0] = 0;
for (int j = 0; rowZero && j < n; j++)
matrix[0][j] = 0;
}
}为了达到O(1)的空间复杂度,我们采用了这种优化手段。然而,这种做法却增加了代码的复杂度并降低了可读性。这证明了在编程和算法设计中,往往需要在各种因素之间做出权衡。没有完美的解决方案,关键在于如何根据实际需求做出恰当的选择与牺牲!