https://www.wolai.com/curry00/fzTPy3kSsMDEgEcdvo4G5w
https://www.bilibili.com/video/BV1Kr4y1i7ru/?p=69
https://jimhackking.github.io/%E8%BF%90%E7%BB%B4/MySQL%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0/#%E7%B4%A2%E5%BC%95
索引是一种用于快速查询和检索数据的数据结构,排序好的数据结构。
优点:加快检索速度;通过创建唯一性索引,可以保证行数据的唯一性;通过索引列对数据进行排序,降低数据排序的成本,降低CPU的消耗
缺点:创建和维护索引需要耗费时间,本身存储也要耗费一定空间
mysql索引类型
- 按「数据结构」分类:B+tree索引、Hash索引、Full-text全文索引(是一种通过建立倒排索引,快速匹配文档的方式)、R-tree空间索引(空间索引是MyISAM引擎的一个特殊索引类型,主要用于地理空间数据类型,通常使用较少)。
- 按「物理存储」分类:聚簇索引(主键索引)、二级索引(辅助索引)。
- 二级索引(Secondary Index)就是非聚簇索引,是因为二级索引的叶子节点 存储的数据是主键。也就是说,通过二级索引,可以定位主键的位置。
- 主键索引就是聚簇索引,叶子节点存储就是数据
- 按「字段特性」分类:主键索引、唯一索引、普通索引、前缀索引。
注意主键索引不允许为null,不允许相同,唯一索引允许多个null但不能相同,普通索引允许为null也允许相同,前缀索引只适用于字符串类型的数据,前缀索引是对文本的前几个字符创建索引。 - 按「字段个数」分类:单列索引、联合索引。
建立在单列上的索引称为单列索引,比如主键索引;
建立在多列上的索引称为联合索引;
不同引擎对索引的支持情况

索引数据结构
哈希表、有序数组、B+树、B树、红黑树,二叉树
-
哈希表:只适用于等值查询的场景,用这种索引做不了范围查询,必须全表扫描。查询效率高
-
有序数组:有序数组在等值查询和范围查询场景中的性能就都非常优秀,但是一旦更新数据就得挪动后面的元素,成本太高
-
二叉搜索树:为了维持 O(log(N)) 的查询复杂度,需要保持这棵树是平衡二叉树。为了做这个保证,更新的时间复杂度也是 O(log(N))。
二叉树是搜索效率最高的,但是实际上大多数的数据库存储却并不使用二叉树。其原因是,索引不止存在内存中,还要写到磁盘上。你可以想象一下一棵 100 万节点的平衡二叉树,树高 20。一次查询可能需要访问 20 个数据块。 -
B树:在二分查找树的基础上,增加单个节点的数据存储数量,同时增加了树的子节点数,一次计算可以把查找范围缩小更多。
插入节点过程:中间节点向上分裂,某个分支超过最大节点数了,最中间的节点,加入根节点中去 https://www.cs.usfca.edu/~galles/visualization/BTree.html(可视化演示网站)
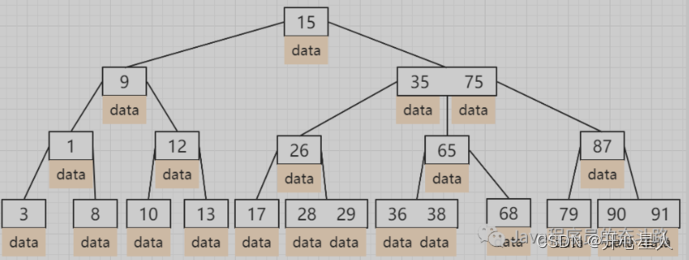
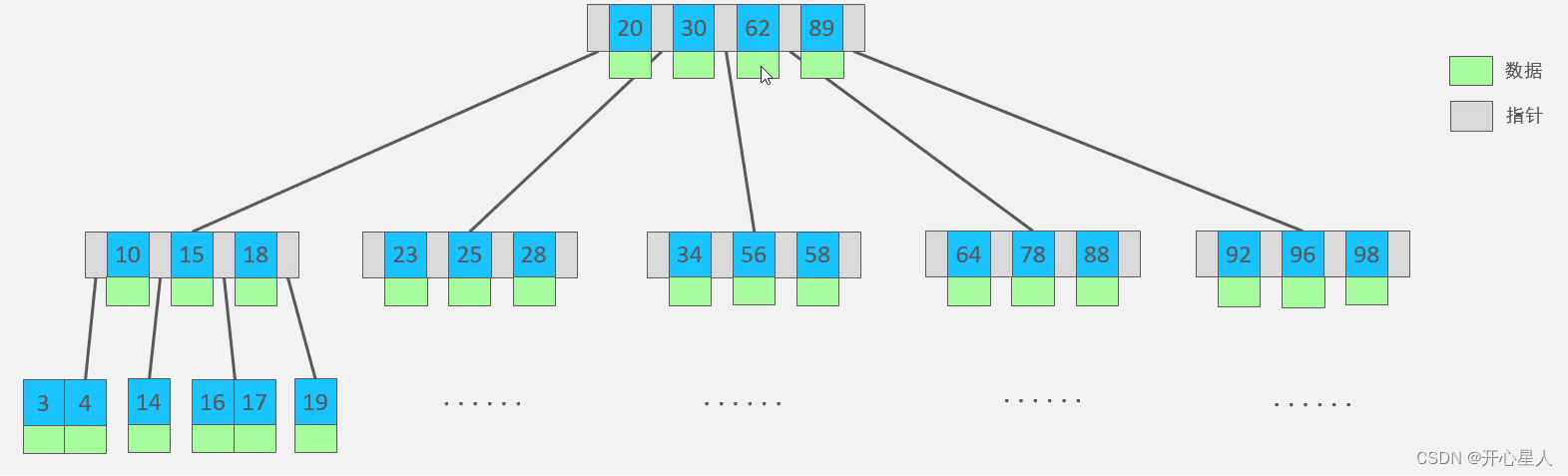
但是非叶子节点会存放索引数据和业务数据,为了查找对比计算,需要把数据加载到内存以及 CPU 高速缓存中时,都要把索引数据和无关的业务数据全部查出来。如果所对比的节点不是所查的数据,那么这些加载进内存的业务数据就毫无用处,全部抛弃。
-
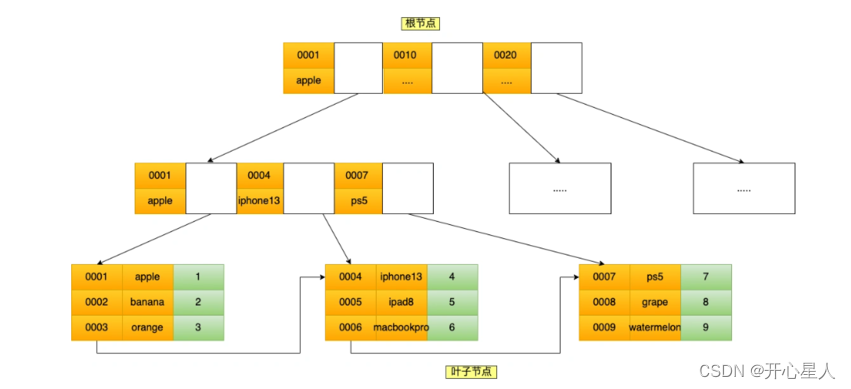
B+ 树:为了拆分索引数据与业务数据的平衡多叉树。非叶子节点只保存索引数据,叶子节点保存索引数据与业务数据,叶子结点形成双向链表,所有元素都会出现在叶子节点。这样即保证了叶子节点的简约干净,数据量大大减小,又保证了最终能查到对应的业务数。既提高了单次 I/O 数据的有效性,又减少了 I/O 次数,还实现了业务。
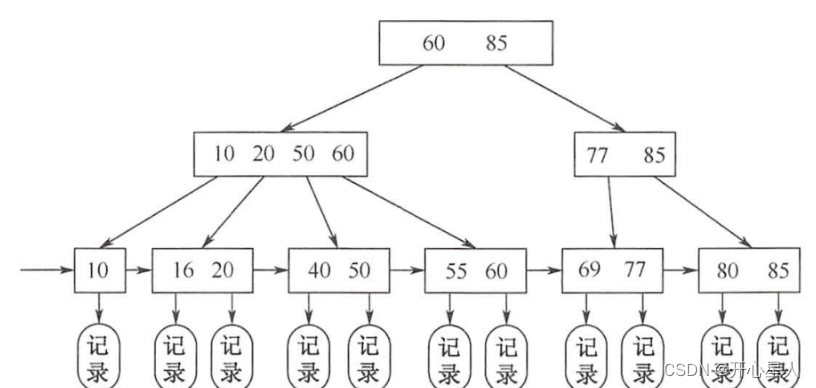
-
红黑树:红黑树就是介于完全不平衡和完全平衡之间的一种二叉树,可以解决二叉树的这个问题(二叉树缺点:顺序插入时,会形成一个链表,查询性能大大降低。大数据量情况下,层级较深,检索速度慢,),通过每个节点有红黑两种颜色、从节点到任意叶子节点会经过相同数量的黑色节点等一系列规则,实现了树的层数最大也只会有两倍的差距,这样既能提高插入和删除的效率,又能让树相对平衡从而有还不错的查询效率。
从整体上讲,红黑树就是一种中庸之道的二叉树,但是用来当mysql的索引还是有问题,用红黑树存放100万个数据,把树放满,这个树的高度会越变越高和二叉搜索树一样
1、B树和B+树的区别
- B+树所有的数据都会出现在叶子节点,B+叶子节点有所有索引的冗余和其对应的数据,非叶子节点没有数据,B树没有冗余,非叶子节点有数据
- B树检索的过程就相当于对于范围内的每个节点的关键字做二分查找,没到达叶子节点可能检索就结束了,检索B+树最后肯定会查询到底,效率比较稳定
- B+树叶子节点之间相互之间也构成一个双向链表,B树没有。所以B树进行范围查询需要找到查询的下限,然后进行中序遍历。B+树直接对链表进行遍历就行
2、为什么mysql使用B+树?
- B+树非叶子节点不放数据只放索引,所以可以存放更多的索引,比B树更矮胖,所以IO次数就比较少
- B+树有很多冗余节点,所以插入、删除的效率就比较高,而B树删除插入调整很多
- B+树叶子节点用双向链表相互连接了起来,所以范围查询效率比较高
3、MyISAM和InnoDB引擎中的B+树区别是什么?
- MyISAM不管是不是主键索引,使用的都是非聚簇索引(叶子节点的data部分放数据记录的地址)
- InnoDB主键索引使用聚簇索引(叶子节点部分就是数据),二级索引则是非聚簇索引
聚簇索引和非聚簇索引
- 聚簇索引:
优点:查询速度快,对主键的排序查找和范围查找速度快
缺点:依赖有序数据,更新代价比较大 - 非聚簇索引:
优点:更新代价小
缺点:依赖有序的数据,可能会二次查询(回表)
1、什么是回表?
如果我用 product_no 二级索引查询商品,如下查询语句:
select * from product where product_no = '0002';
会先检二级索引中的 B+Tree 的索引值(商品编码,product_no),找到对应的叶子节点,然后获取主键值,然后再通过主键索引中的 B+Tree 树查询到对应的叶子节点,然后获取整行数据。这个过程叫「回表」,也就是说要查两个 B+Tree 才能查到数据。
2、创建表时,InnoDB 存储引擎会怎么选择索引?
- 如果有主键,默认会使用主键作为聚簇索引的索引键(key)
- 如果没有主键,就选择第一个不包含 NULL 值的唯一列作为聚簇索引的索引键(key)
- 在上面两个都没有的情况下,InnoDB 将自动生成一个隐式自增 id 列作为聚簇索引的索引键(key)